Problem: 1
The points \( A(-9, -1) \) and \( B(3, -5) \) lie on the circumference of a circle. Show that the centre of the circle lies on the line \( y = 3x + 6 \) .
Solution
Let \( (a, b) \) be the centre of the circle. Hence the equation of the circle is |
Problem: 2
Find the equation of the circle that passes through the point \((5,-2)\) and has the same centre as the circle \(x^2+y^2-4 x+8 y-40=0\) .
Solution

\begin{aligned} &x^2+y^2-4 x+8 y-40=0\\\\ & x^2-4 x+y^2+8 y=40 \\\\ & x^2-4 x+2^2+y^2+8 y+4^2=40+2^2+4^2 \\\\ & (x-2)^2+(y+4)^2=60 \end{aligned} |
Problem: 3
A circle passes through the points \(P(-2,0)\), \(Q(3,5)\) and \(R(6,2)\). Show that \(PR\) is a diameter of the circle and find the equation of this circle.
Solution
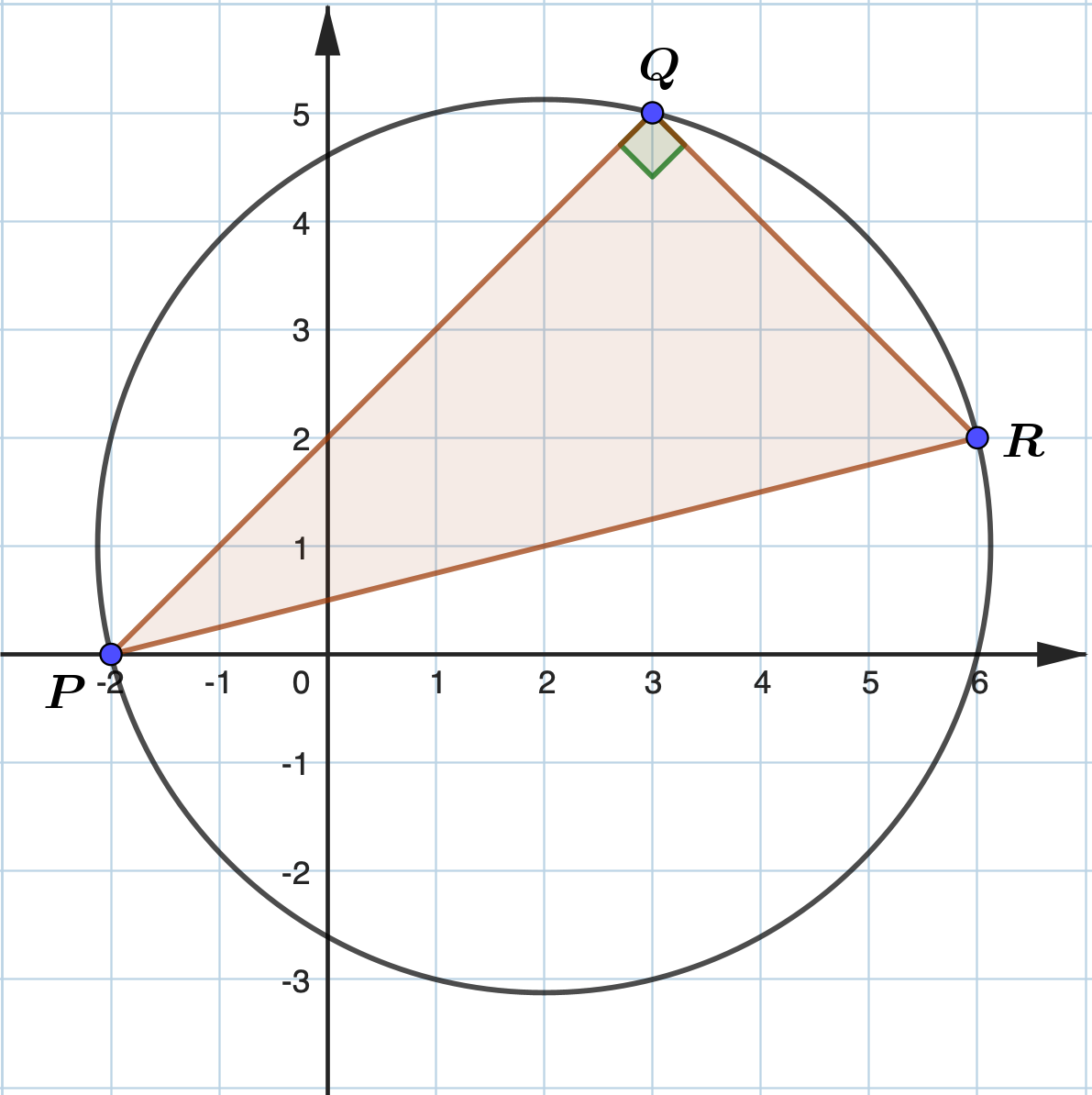
\[
m_{PQ} \times m_{QR} = \frac{5-0}{3+2} \times \frac{2-5}{6-3} = -1
\]
Let the centre of the circle be \(O\).
\(OP = \sqrt{(2+2)^2 + 1^2} = \sqrt{17}\) |
Problem: 4
A circle passes through the points \((-1,-4)\) and \((3,2)\) and has radius \(\sqrt{26}\) . Find the two possible equations for this circle.
Solution
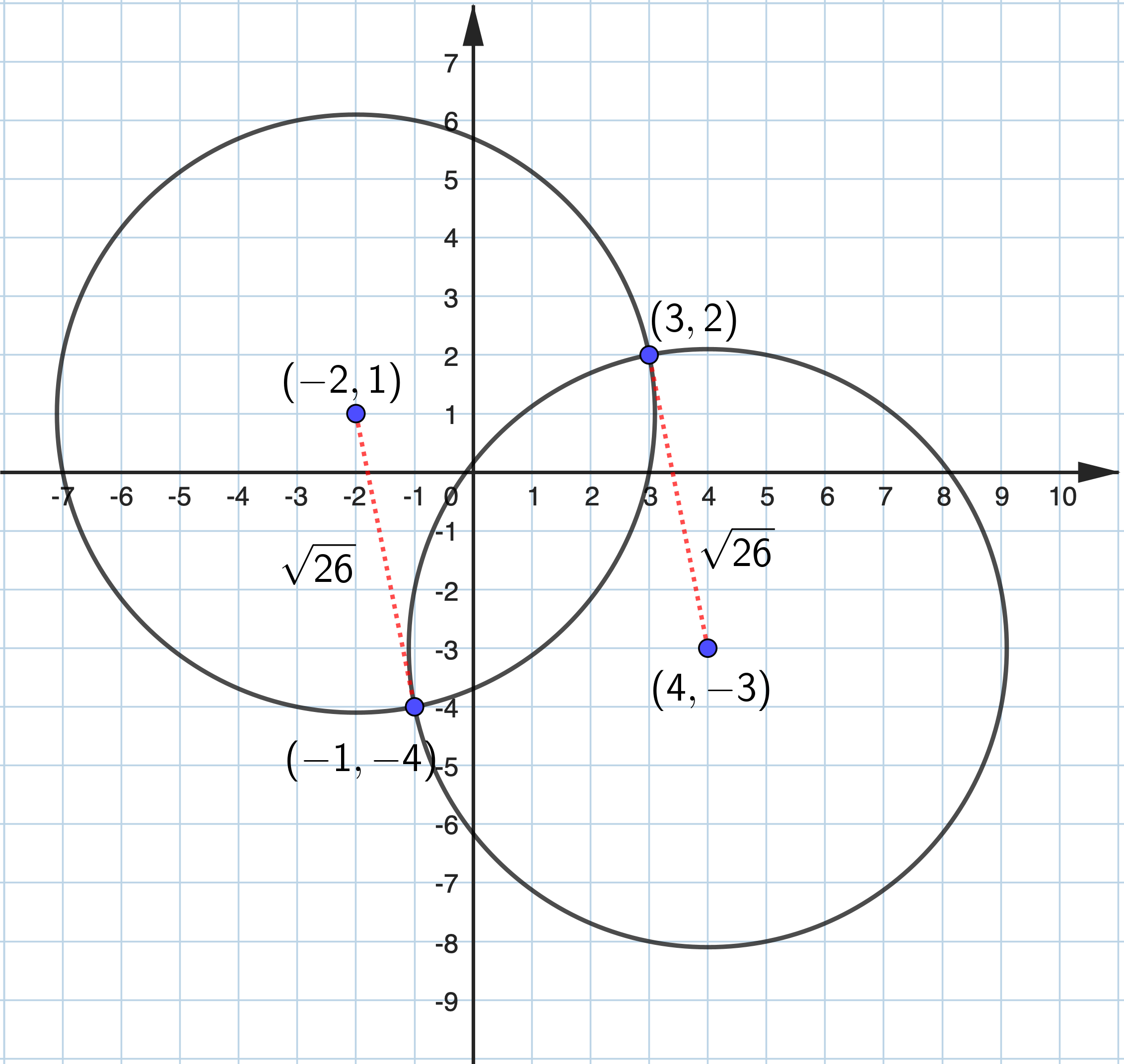
Let the centre of the circle be \((h, k)\) Hence the equation of the circle is \((x-h)^2+(y-k)^2=2 6\) . \((-1,-4)\) and \((3,2)\) lie on the circumference of the circle. \begin{aligned} \therefore \quad & (-1-h)^2+(-4-k)^2=26 \\ & 1+2 h+h^2+16+8 k+k^2=26 \\ & h^2+k^2+2 h+8 k=9 \quad \ldots (1)\\ & (3-h)^2+(2-k)^2=26 \\ & 9-6 h+h^2+4-4 k+k^2=26 \\ & h^2+k^2-6 h-4 k=13 \quad \ldots (2)\\ & 8 h+12 k=-4 \\ & 2 h+3 k=-1 \\ \therefore \quad & h=\frac{-3 k-1}{2} \end{aligned} Substituting \(\displaystyle h=\frac{-3 k-1}{2}\) in equation (1), \begin{aligned} & \frac{9 k^2+6 k+1}{4}+k^2-3 k-1+8 k=9 \\ & 9 k^2+6 k+1+4 k^2-12 k-4+32 k-36=0 \\ & 13 k^2+26 k-39=0\\ & k^2+2 k-3=0 \\ & (k+3)(k-1)=0 \\ & k=-3 \text { or } k=7 \end{aligned} When \(\displaystyle k=-3, h=\frac{9-1}{2}=4\) . When \(\displaystyle k=1, h=\frac{-3-1}{2}=-2\) . Thus, the possible equations of the circle are \((x-4)^2+(y+3)^2=26 \text { or }(x+2)^2+(y-1)^2=26\) . |
Problem: 5
The equation of a circle is \((x-4)^2+(y+3)^2=41\) . Show that the point \(P(8,2)\) lies on the circle and find the equation of the tangent to the circle at the point \(P\) .
Solution
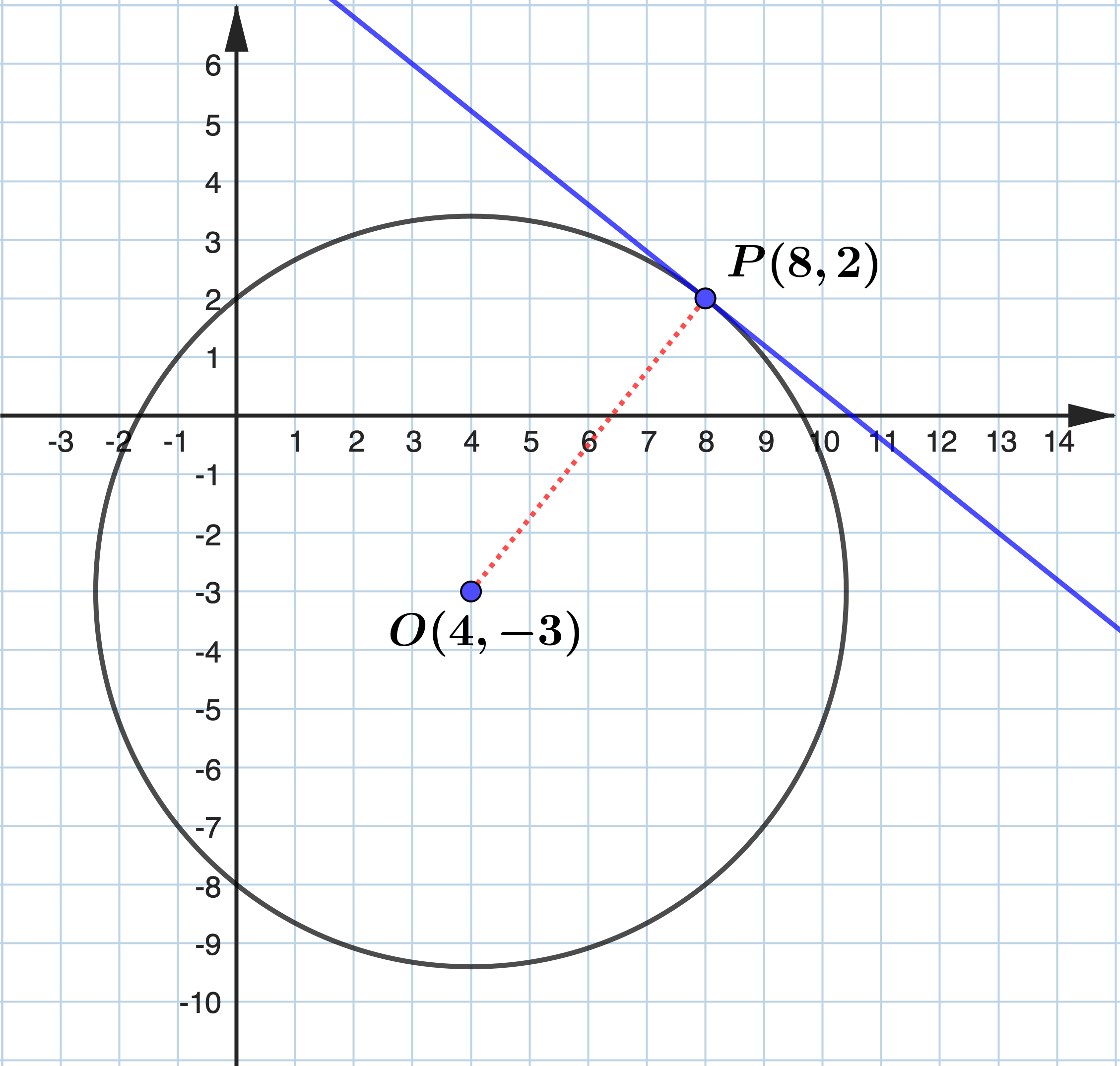
Circle: \((x-4)^2+(y+3)^2=41\) When \(x=8\) and \(y=2\) , \((8-4)^2+(2+3)^2=16+25=41\) Hence, \(P(8,2)\) lies on the circle. Let the centre of the circle be \(O\) . Therefore, \(O\) has coordinates \((4,-3)\) . gradient of \(\displaystyle O P=\frac{2-(-3)}{8-4}=\frac{5}{4}\) So, the gradient of tangent passing through \(P\) is \(-\displaystyle\frac{4}{5}\) . The equation of tangent to the circle at \(P\) is \begin{aligned} & y-2=-\frac{4}{5}(x-8) \\ & 4 x+5 y=42 \end{aligned} |
Problem: 6
A circle has radius 5 units and passes through the point \((2,-6)\) . The \(y\) -axis is a tangent to the circle. Find the possible equations of the circle.
Solution

Let the centre of the circle be \((h, k)\) . Since the \(y\) -axis is tangent to the circle whose radius is 5, \(h=5\) . Hence, the equation of the circle is \((x-5)^2+(y-k)^2=25\) . \((2,-6)\) lies on the circle \begin{aligned} \therefore \quad & (2-5)^2+(-6-k)^2=25 \\ & (-6-k)^2=15 \\ \therefore \quad & -6-k=-4 \text { or }-6-k=4 \\ \therefore \quad & k=-2 \text { or } k=-10 \end{aligned} Thus, the possible equations of the circle are \( (x-5)^2+(y+2)^2=25\) or\( (x-5)^2+(y+10)^2=25\) . |
Problem: 7
Find the equation of the circle which passes through the points \((7,4)\) and \((0,5)\) and has its centre lying on the line \(x+2 y=5\) .
Solution
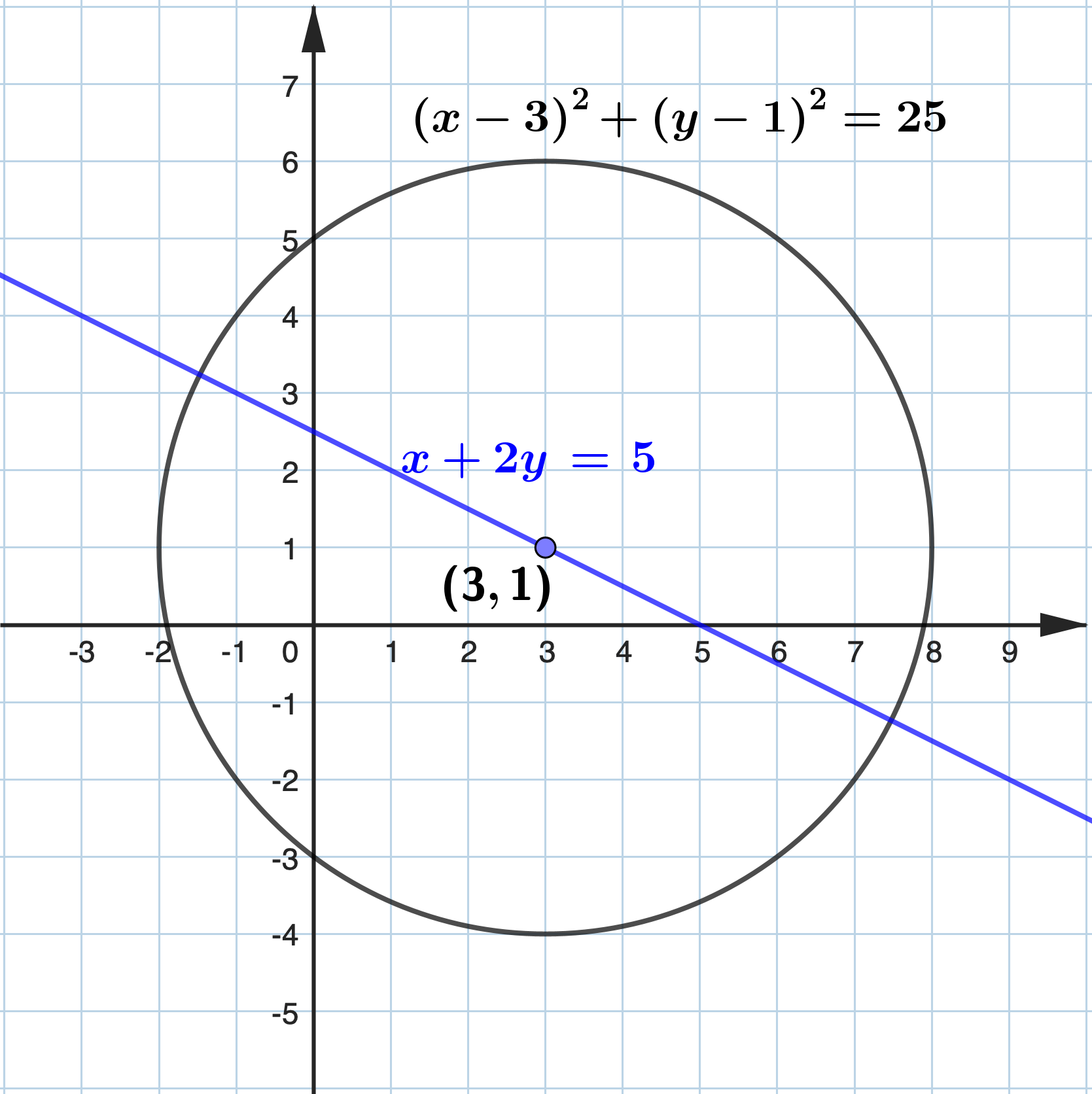
Let the centre of the circle be \((a, b)\) . Since \((a, b)\) lies on the live \(x+2 y=5\) , \begin{aligned} & a+2 b=5 \\ \therefore\quad & a=5-2 b \end{aligned} Let the radius be \(r\) . The equation of the circle is \((x-(5-2 b))^2+(y-b)^2=r^2\) Since the circle passes through \((7,4)\) and \((0,5)\) , \begin{aligned} & (7-5+2 b)^2+(4-b)^2=r^2 \\ & 4+8 b+4 b^2+16-8 b+b^2=r^2 \\ & 5 b^2+20=r^2 \ldots(1) \end{aligned} |
Problem: 8
\(A\) is the point \((-3,4)\) and \(B\) is the point \((1,12)\) .
(a) Find the equation of the line through \(A\) and \(B\) .
(b) Show that the perpendicular bisector of the line \(A B\) is \(x+2 y=15\) .
(c) A circle passes through \(A\) and \(B\) and has its centre on the line \(x=9\) . Find the equation of this circle.
Solution
|
(a) gradient of \(\displaystyle A B=\frac{12-4}{1-(-3)}=\frac{8}{4}=2\) . Equation of \( A B: \quad y-12=2(x-1) \Rightarrow y=2 x+10\) . (b) Let the perpendicular bisector of \(A B\) be \(l\) . gradient of \(l=-\displaystyle\frac{1}{2}\) Midpoint of \(\displaystyle A R B=\left(\frac{-3+1}{2}, \frac{4+12}{2}\right)=(-1,8)\) \begin{aligned} \text{Equation of } l : &~ y-8=-\frac{1}{2}(x+1) \\ & 2 y-16=-x-1 \\ & x+2 y=15 \end{aligned} (c) Let the required circle be \(C\) and its radius be \(r\) . Hence, the centre of \(C\) lies on both lines \(x+2 y=15\) and \(x=9\) . \(9+2 y=15 \Rightarrow y=3 .\) Centre of \(C:(9,3)\) \(r=\sqrt{(9+3)^2+(3-4)^2}=\sqrt{145}\) Equation of \(C:(x-9)^2+(y-3)^2=145\) |
Problem: 9
A circle \(C\) has centre \(A(3,4)\) and passes through the point \(B(7,10)\) .
(a) Find the length\(A B\) giving your answer in exact form.
(b) Write down the equation of circle\(C\) .
The line \(L\) is a tangent to circle\(C\) at the point \(B\) .
(c) Find the equation for \(L\) , giving your answer in the form \(a x+b y+c=0\) where \(a, b\) and \(c\) are integers.
Solution
|
(a) \(A B=\sqrt{(7-3)^2+(10-4)^2}=\sqrt{52}=2 \sqrt{13}\) (b) Equation of C: \((x-3)^2+(y-4)^2=52\) (c) gradient of \(A B=\frac{10-4}{7-3}=\frac{3}{2}\) \(\therefore\ \) gradient of \(L=-\frac{2}{3}\) Equation of \(L: \quad y-10=-\frac{2}{3}(x-7) \Rightarrow 2 x+3 y-28=0\) |
Problem: 10
A circle has centre \(C(-3,5)\) and passes through the origin.
(a )Find an equation for this circle.
The circle crosses the \(x\) axis at the origin and at the point \(A\) .
(b) Determine the coordinates of \(A\) .
Solution
(a) centre:\(C(-3,5)\) Let the radius of the circle be \(r\) . \(r=O C=\sqrt{(-3-0)^2+(5-0)^2}=\sqrt{34}\) \(\therefore \) Equation of the circle: \((x+3)^2+(y-5)^2=34\) (b) When the circle crosses the \(x\) -axis, \(y=0\) \begin{aligned} \therefore\quad & (x+3)^2+(0-5)^2=34 \\ & (x+3)^2=9 \Rightarrow x+3= \pm 3 \\ \therefore \quad & x=-6 \text { or } x=0 \end{aligned} \( \therefore \) A has coordinates \((-6,0)\) . |
