Problem: 11
The line \(y=x-3\) intersects the circle \((x-3)^2+(y+2)^2=20\) at two points \(P\) and \(Q\). Find the length of \(P Q\).
Solution
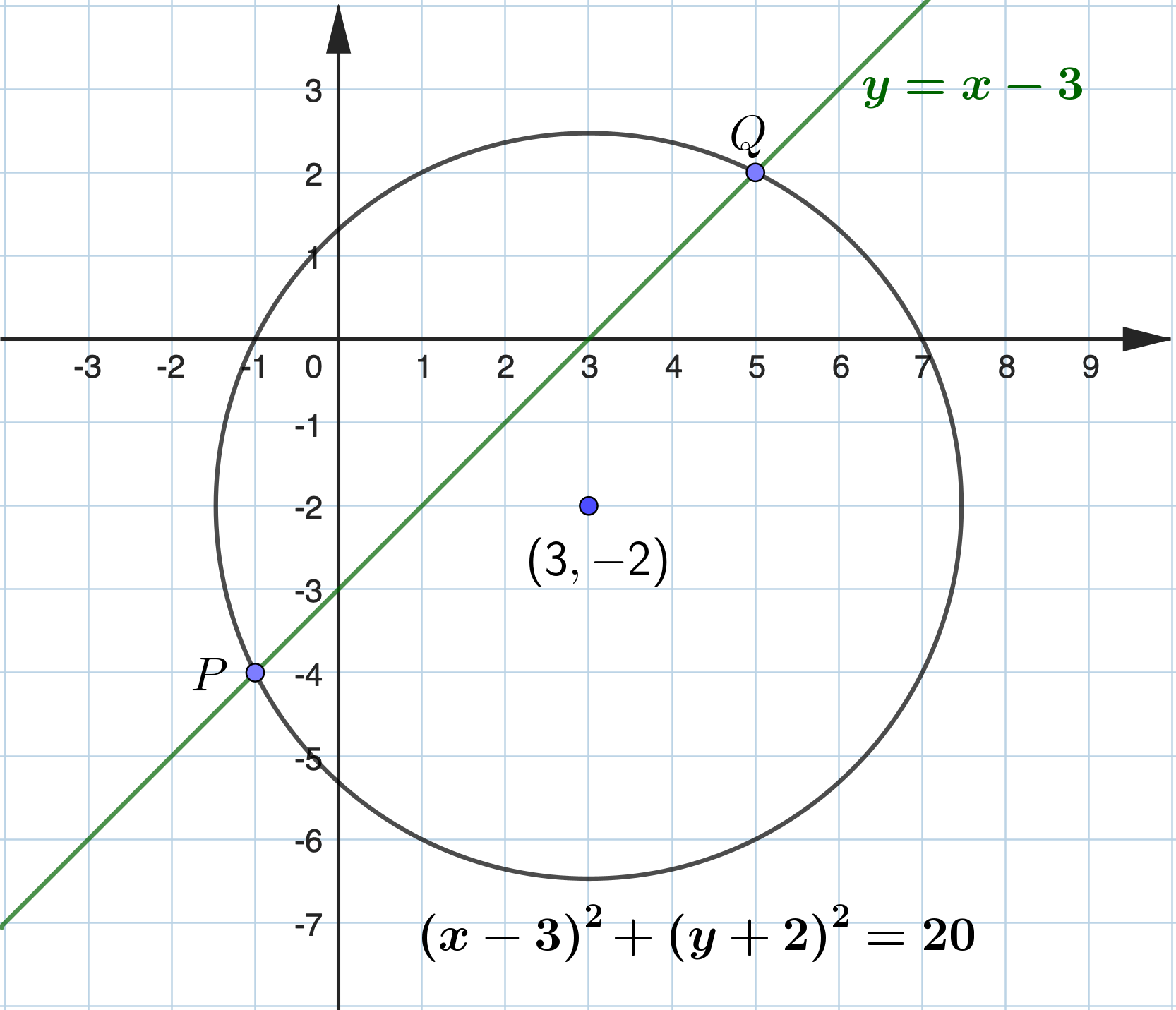
\begin{aligned} & (x-3)^2+(x-3+2)^2=20 \\ & x^2-6 x+9+x^2-2 x+1-20=0 \\ & 2 x^2-8 x-10=0 \\ & x^2-4 x-5=0 \\ & (x+1)(x-5)=0 \\ & x=-1 \text { or } x=5 \\ & x=-1 \Rightarrow y=-4 \\ & x=5 \Rightarrow y=2 \end{aligned} Hence, \(P\) and \(Q\) have coordinates \((-1,-4)\) and \((5,2)\). \(P Q=\sqrt{(5+1)^2+(2+4)^2}=6 \sqrt{2}\) |
Problem: 12
Explain why the line \(P4 y=x+26\) is a tangent to the circle \(Px^2+y^2+10 x-2 y+9=0\) and find the coordinates of the point where the line touches the curve.
Solution
|
Line: \(4 y=x+26 \Rightarrow x=4 y-2 b\) Circle: \(x^2+y^2+10 x-2 y+9=0\) At the point of intersection of the line and circle, \begin{aligned} & (4 y-26)^2+y^2+10(4 y-26)-2 y+9=0 \\ & 16 y^2-208 y+676+y^2+40 y-260-2 y+9=0 \\ & 17 y^2-170 y+425=0 \\ & y^2-10 y+25=0 \\ & (y-5)^2=0\Rightarrow y=5\\ \therefore\quad& x=-6 \end{aligned} Hence the live intersects the circle at only one point \((5,-6)\). Thus, the line is tangent to the circle. |
Problem: 13
The circles \((x-10)^2+(y-5)^2=25\) and \((x-20)^2+(y-10)^2=100\) intersect at the points \(P\) and \(Q\).
(a) Find the length of the line \(P Q\).
(b) Find the equation of the common chord \(P Q\).
Solution
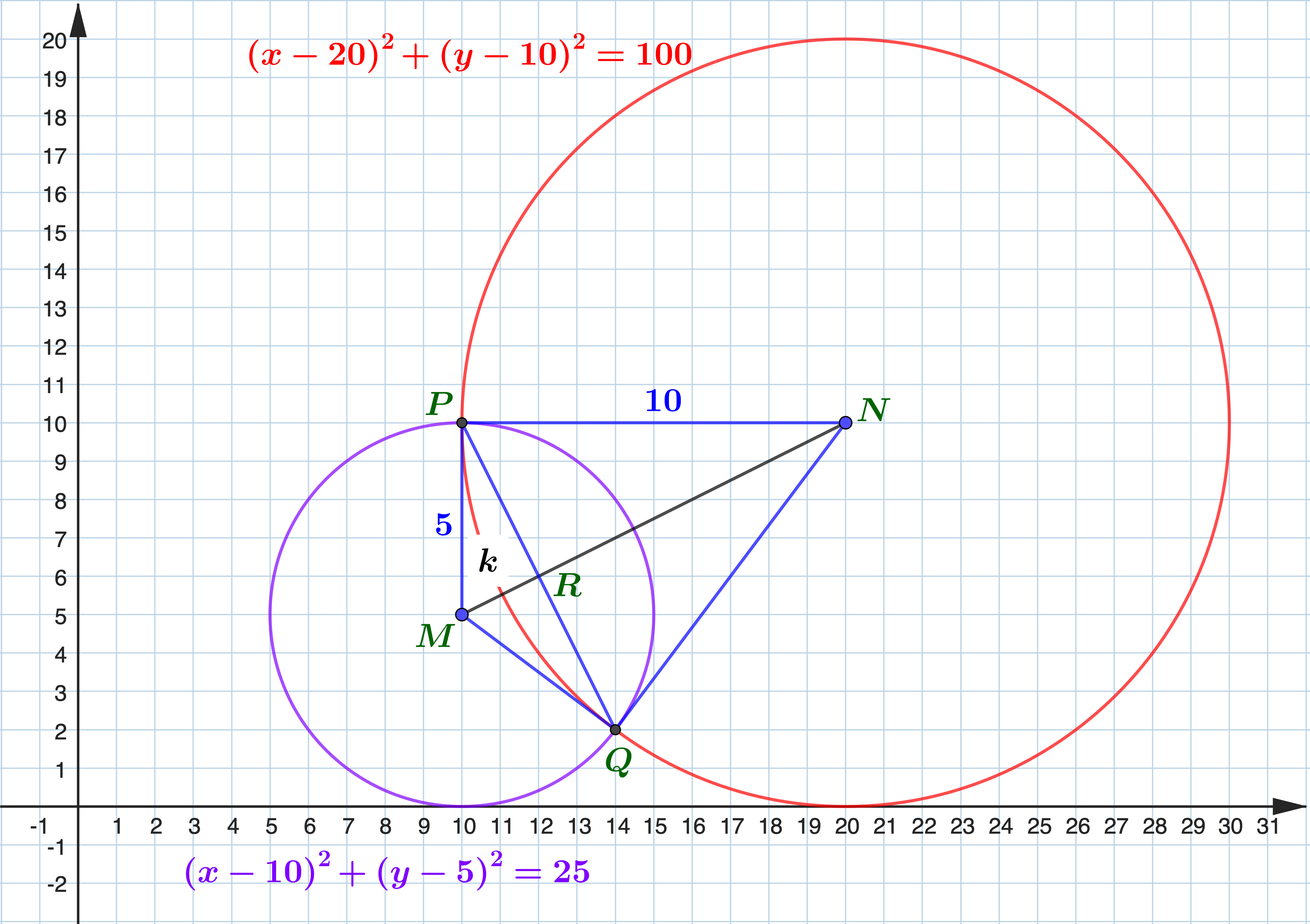
Method 1Circle 1: \(\quad(x-10)^2+(y-5)^2=25\) centre: \((10,5)\), radius \(=5\) Circle 2: \(\quad(x-20)^2+(y-10)^2=100\) centre: \((20,10)\), radius \(=10\) Let the centre of the two circles be \(M(10,5)\) and \(N(20,10)\) and the radii of the circles be \(r_1=5 \) and \(r_2=10 \). \(M N=\sqrt{(20-10)^2+(10-5)^2}=5 \sqrt{5} \) Let the point of intersection of \(P Q\) and \(MN\) be \(R\). Let \(MR=k\). \(\therefore \quad R N=5 \sqrt{5}-k\) \begin{aligned} \therefore \quad & P R^2=5^2-k^2 \text { or } \\ & P R^2=10^2-(5 \sqrt{5}-k)^2 \\ \therefore \quad & 5^2-k^2=10^2-(5 \sqrt{5}-k)^2 \\ & 25-k^2=100-125+10 \sqrt{5} k-k^2 \\ & 10 \sqrt{5} k=50 \Rightarrow k=\sqrt{5} \\ \therefore \quad& P R^2=25-5=20 \Rightarrow P R=2 \sqrt{5} \\ \therefore\quad & P Q=2 P R=4 \sqrt{5} \end{aligned} gradient of \(M N=\displaystyle\frac{10-5}{20-10}=\displaystyle\frac{1}{2}\) \(\therefore\quad \) gradient of \(P Q=-2\quad (\because \ P Q \perp \mathrm{MN})\) \(\displaystyle\frac{M R}{R N}=\displaystyle\frac{\sqrt{5}}{4 \sqrt{5}}=\displaystyle\frac{1}{4}\) By section formula, \( R=\left(\displaystyle\frac{4 \times 10+20}{5}, \displaystyle\frac{4 \times 5+10}{5}\right)=(12,6)\) Equation of \(PQ\) is \(y-6 =-2(x-12) \Rightarrow y=30-2 x .\) Method 2\begin{aligned} & \text{Circle} 1: (x-10)^2+(y-5)^2=25\\ & x^2-20 x+100+y^2-10 y+25-25=0 \\ & x^2+y^2-20 x-10 y+100=0 \ldots(1) \end{aligned} \begin{aligned} & \text{Circle} 2:(x-20)^2+(y-10)^2=100\\ & x^2-40 x+400+y^2-20 y+100-100=0 \\ & x^2+y^2-40 x-20 y+400=0 \ldots(2) \end{aligned} At the points of intersection two circles, \begin{aligned} & x^2+y^2-20 x-10 y+100=x^2+y^2-40 x-20 y+400 \\ & 10 y=300-20 x \Rightarrow y=30-2 x \ldots(3) \end{aligned} Substituting \(y=30-2 x\) in equation ( 1 ) \begin{aligned} & x^2+(30-2 x)^2-20 x-10(30-2 x)+100=0 \\ & x^2+300-120 x+4 x^2-20 x-300+20 x+100= \\ & 5 x^2-120 x+700=0 \\ & x^2-24 x+140=0 \\ & (x-10)(x-14)=0 \\ & x=10 \text { or } x=14 \\ & x=10 \Rightarrow y=10 \\ & x=14 \Rightarrow y=2 . \\ & P Q=\sqrt{(14-10)^2+(2-10)^2}=4 \sqrt{5} \end{aligned} Equation of \(P Q: \quad y=30-2 x\). |
Problem: 14
Explain why the circles \((x+7)^2+(y+2)^2=4\) and \((x+7)^2+(y+5)^2=25\) touch at one point. Determine whether they touch internally or externally and find the coordinates of the point at which they touch.
Solution
|
Circle 1: \((x+7)^2+(y+2)^2=4\) centre: \((-7,-2)\), radius \(=2\) Circle 2: \((x+7)^2+(y+5)^2=25 \ldots(2)\) centre: \((-7,-5)\), radius \(=5\) distance between two centres \(=\sqrt{(-7+7)^2+(-5+2)^2}=3\) sum of radii \(=7\) difference of radii \(=3\) Hence the two circle touch internally each other. Fromequation 1, we have \((x+7)^2=4-(y+2)^2\) Substituting equation 3 in equation (2) \begin{aligned} & 4-(y+2)^2+(y+5)^2=25 \\ & 4-y^2-4 y-4+y^2+10 y+25=25 \\ \therefore \quad & 6 y=0 \Rightarrow y=0 \\ \therefore \quad & (x+7)^2=4-(0+2)^2=0 \\ \therefore \quad & x=-7 \end{aligned} Hence the two circles touch each other at the point \((-7,0)\). |
Problem: 15
The line \(2 x+y=6\) intersects the circle \(x^2+y^2-12 x-8 y+27=0\) at the points \(A\) and \(B\).
(a) Find the coordinates of the points \(A\) and \(B\).
(b) Find the equation of the perpendicular bisector of \(A B\).
(c) The perpendicular bisector of \(A B\) intersects the circle at the points\(P\) and \(Q\). Find the exact coordinates of \(P\) and \(Q\).
(d) Find the exact area of quadrilateral \(A P B Q\).
Solution
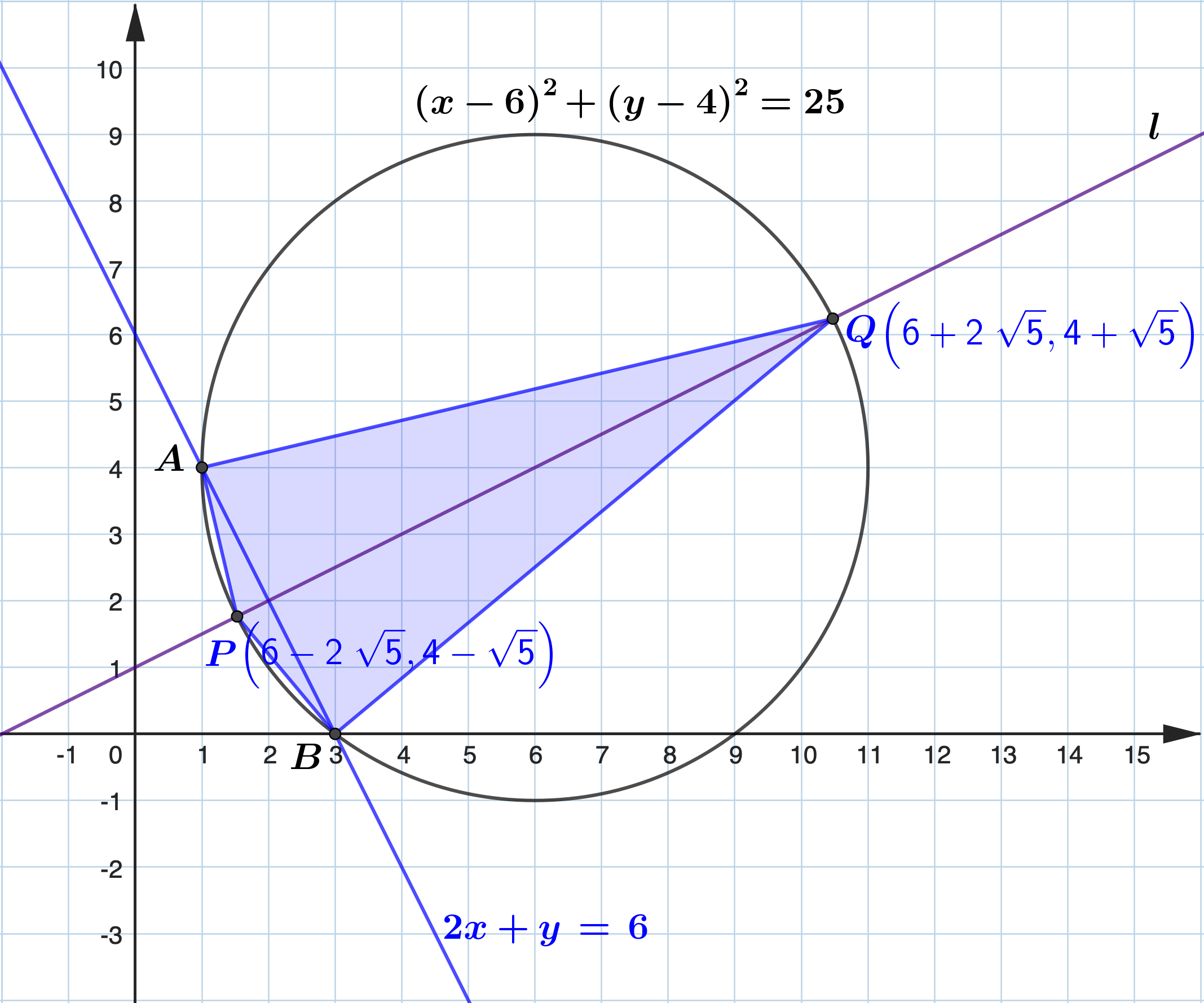
Line: \(2 x+y=6 \Rightarrow y=6-2 x\) Circle: \(x^2+y^2-12 x-8 y+27=0\) At the point of intersection of tho line and circle, \begin{aligned} & x^2+(6-2 x)^2-12 x-8(6-2 x)+27=0 \\ & x^2+36-24 x+4 x^2-12 x-48+16 x+27=0 \\ & 5 x^2-20 x+15=0 \\ & x^2-4 x+3=0 \\ & (x-1)(x-3)=0 \\ & x=1, x=3 \\ & x=1 \Rightarrow y=4 \\ & x=3 \Rightarrow y=0 \end{aligned} Thus, \(A\) and \(B\) have coordinates \((1,4)\) and \((3,0)\) respectively. Let \(M\) be the midpoint of \(A B\) and \(l\) be the perpendicular injector of \(A B\). \(\therefore\ M=\left(\displaystyle\frac{1+3}{2}, \displaystyle\frac{4+0}{2}\right)=(2,2)\) gradient of \(A B=\displaystyle\frac{4-0}{1-3}=-2\) gradient of \(l=\displaystyle\frac{1}{2}\) Equation of \(l\) : \(y-2=\displaystyle\frac{1}{2}(x-2) \Rightarrow 2 y-x=2 \text { (or) } x=2 y-2\) At the point of intersection of \(l\) and circle, \begin{aligned} & (2 y-2)^2+y^2-12(2 y-2)-8 y+27=0 \\ & 4 y^2-8 y+4+y^2-24 y+24-8 y+27=0 \\ & 5 y^2-40 y+55=0\\ & y^2-8 y+11=0 \\ & y^2-8 y+16=5 \\ & (y-4)^2=5 \\ & y=4 \pm \sqrt{5} \\ & y=4-\sqrt{5}, x=6-2 \sqrt{5} \\ & y=4+\sqrt{5}, x=6+2 \sqrt{5} \end{aligned} P and Q have coordinates \((6-2 \sqrt{5}, 4-\sqrt{5}) \text { and }(6+2 \sqrt{5}, 4+\sqrt{5}) \). The circle \(x^2+y^2-12 x-8 y+27=0\) has radius \(v=\sqrt{36+16-27}=5\). Since \(P Q\) is the diameter of the circle, \(P Q=10\). \(A B=\sqrt{(3-1)^2+(0-4)^2}=2 \sqrt{5}\) area of \(A P B Q=\displaystyle\frac{1}{2} \times A B \times P Q=\displaystyle\frac{1}{2} \times 2 \sqrt{5} \times 10=10 \sqrt{5}\) |
Problem: 16
Find the set of values of \(m\) for which the line \(y=m x+3\) intersects the circle \(x^2+y^2-10 x-8 y+28=0\) at two distinct points.
Solution
|
Line: \(y=m x+3\) Circle: \(x^2+y^2-10 x-8 y+28=0\) At the point of intersection the line and circle, \begin{aligned} & x^2+(m x+3)^2-10 x-8(m x+3)+28=0 \\ & x^2+m^2 x^2+6 m x+9-10 x-8 m x-2 y+28=0 \\ & \left(m^2+1\right) x^2-2(m+5) x+13 \end{aligned} Since the line intersects the circle at two distinct point, discriminant \(>0\) \begin{aligned} & 4(m+5)^2-4\left(m^2+1\right)(13)>0 \\[-1mm] & -6 m^2+5 m+6>0 \\[-1mm] & 6 m^2-5 m+6<0 \\ & (3 m+2)(2 m-3)<0 \\ \therefore \quad& -\displaystyle\frac{2}{3}<m<\displaystyle\frac{3}{2} \end{aligned} |
Problem: 17
(a) Use each of the following methods to show that the four points \(A(-4,-2)\), \(B(-2,2), C(5,1)\) and \(D(4,-6)\) lie on a circle.
Methods
(i) Use the property that the perpendicular bisector of two chords on a circle intersect at the centre of the circle to find the equation of the circle passing through three of the points and then show that the fourth point lies on this circle.
(ii) Use three of the points to write down three simultaneous equations. Solve the equations and then show that the fourth point lies on this circle.
(iii) Show that opposite angles in the quadrilateral \(A B C D\) add up to \(180^{\circ}\) which means that \(A B C D\) is a cyclic quadrilateral. Hence the four points lie on a circle.
(iv) Show that angle \(B A D=90^{\circ}\). Hence \(B D\) must be a diameter of the circle (angles in a semi-circle) and the centre of the circle is the midpoint of \(B D\). Then show that the fourth point, \(C\), lies on this circle.
(b) Find out about Ptolemy's theorem and use it to show that the points\(A, B, C\) and \(D\) lie on a circle.
Solution
Method 1Midpoint of \(A B=\left(\displaystyle\frac{-4-2}{2}, \displaystyle\frac{-2+2}{2}\right)=(-3,0)\) Midpoint of \(A D=\left(\displaystyle\frac{-4+4}{2}, \displaystyle\frac{-2-6}{2}\right)=(0,-4)\) gradient of \(A B=\displaystyle\frac{2+2}{-2+4}=2\) gradient of\(A D=\displaystyle\frac{-6+2}{4+4}=-\displaystyle\frac{1}{2}\) Let the perpendicular bisector of \(A B\) and \(A\) D be \(l_1\) and \(l_2\) respectively. gradient of \(l_1=-\displaystyle\frac{1}{2}\) gradient of \(l_2=2\) Equation of\(l_1\Rightarrow y-0=-\displaystyle\frac{1}{2}(x+3) \Rightarrow y=-\displaystyle\frac{1}{2}(x+3) \ldots(1)\) Equation of \(l_2\Rightarrow y=2 x-4 \ldots(2)\) Solving equations (1) and (2) \begin{aligned} & -\displaystyle\frac{1}{2}(x+3)=2 x-4 \\ & 5 x=5 \Rightarrow x=1 \\ \therefore\quad & y=2-4=-2 \end{aligned} Hence, the centre of the circle passing through \(A, B\) and \(D\) is \((1,-2)\). radius of circle \(=\sqrt{(1+4)^2+(-2+2)^2}=5\) Therefore, the equation of the circle passing through \(A, B\) and \(D\) is \((x-1)^2+(y+2)^2=25\) When \(x=5\) and \(y=1\), \((5-1)^2+(1+2)^2=4^2+3^2=25\) \(\therefore A, B, C\) and \(D\) all lie on a circle. Method 2Let the equation of the circle be \(x^2+y^2+2 g x+2 f y+e=0\) At \(A(-4,-2)\), \begin{aligned} & 16+4-8 g-4 f+e=0 \\ & -8 g-4 f+e=-20 \ldots(1) \end{aligned} At \(B(-2,2)\), \begin{aligned} & 4+4-4 g+4 f+e=0 \\ & -4 g+4 f+e=-8 \ldots(2) \end{aligned} At \(D(4,-6)\), \begin{aligned} & 16+36+8 g-12 f+e=0 \\ & 8 g-12 f+e=-52 \ldots(3) \end{aligned} Equation (1) + Equation (2) \begin{aligned} & -12 g+2 e=-28 \\ & e=6 g-14 \ldots(4) \end{aligned} Substitute \(e=6g-14\) in equations (2) and (3), \begin{aligned} & -4 g+4 f+6 g-14=-8 \\ & g=3-2 f \ldots(5) \\ & 8 g-12 f+6 g-14=-52 \\ & 7 g-6 f=-19 \ldots(6) \\ & 21-14 f-6 f=-19 \Rightarrow f=2 \end{aligned} \begin{aligned} & g=3-2(2)=-1 \\ & e=6(-1)-14=-20 . \end{aligned} The equation of circle passing through \(A, B\) and \(D\) is \(x^2+y^2-2 x+4 y-20=0\) When \(x=5\) and \(y=1\), \(25+1-10+4-20=0\) Hence, the points \(A, B, C\) and \(D\) all lie on a circle. Method 3\begin{aligned} & m_{A B}=\displaystyle\frac{2+2}{-2+4}=2 \\[2mm] & m_{B C}=\displaystyle\frac{1-2}{5+2}=-\displaystyle\frac{1}{7} \\[2mm] & m_{C D}=\displaystyle\frac{-6-1}{4-5}=7 \\[2mm] & m_{A D}=\displaystyle\frac{-6+2}{4+4}=-\displaystyle\frac{1}{2} \\[2mm] \therefore \quad & m_{A B} \cdot m_{A D}=2\left(-\displaystyle\frac{1}{2}\right)=-1 \\ \therefore \quad & A B \perp A D \Rightarrow \angle B A D=90^{\circ} \\ \therefore \quad & m_{B C} \cdot m_{C D}=-\displaystyle\frac{1}{7}(7)=-1 \\ & B C \perp C D \Rightarrow \angle B C D=90^{\circ} \\ \therefore \quad & \angle B A D+\angle B C D=180^{\circ} \end{aligned} \(\therefore\quad A B C D\) is a cyclic quadrilateral. Method 4\begin{aligned} & m_{A B}=\displaystyle\frac{2+2}{-2+4}=2 \\ & m_{A D}=\displaystyle\frac{-6+2}{4+4}=-\displaystyle\frac{1}{2} \\ & m_{A B} \cdot m_{A D}=2\left(-\displaystyle\frac{1}{2}\right)=-1 \\ \therefore \quad & A B \perp A D \Rightarrow \angle B A D=90^{\circ} \end{aligned} \(\therefore \quad B D\) is the diameter of circle passing through \(A, B\) and \(D\). \begin{aligned} \therefore \text { centre } & =\left(\displaystyle\frac{4-2}{2}, \displaystyle\frac{-6+2}{2}\right)=(1,-2) \\ \text { radius } & =\sqrt{(4-1)^2+(-6+2)^2}=5 \end{aligned} \(\therefore\ \) The equation of the circle through \(A, B\) and\(D\) is \((x-1)^2+(y+2)^2=25\) When \(x=5\) and \(y=1\), \((5-1)^2+(1+2)^2=16+9=25.\) \(\therefore\ A, B, C\) and \(D\) all lie on a circle. (b) Ptolemy's TheoremIf a quadrilateral is cyclic then the product of the lengths of its diagonals is equal to the sum of the products of the lengths of the pairs of opposite sides. \begin{aligned} & A(-4,-2), B(-2,2), C(5,1), D(4,-6) \\ & A B=\sqrt{(-2+4)^2+(2+2)^2}=\sqrt{20}=2 \sqrt{5} \\ & B C=\sqrt{(5+2)^2+(1-2)^2}=\sqrt{50}=5 \sqrt{2} \\ & C D=\sqrt{(4-5)^2+(-6-1)^2}=\sqrt{50}=5 \sqrt{2} \\ & A D=\sqrt{(4+4)^2+(-6+2)^2}=\sqrt{80}=4 \sqrt{5} \\ & B D=\sqrt{(4+2)^2+(-6-2)^2}=10 \\ & A C=\sqrt{(5+4)^2+(1+2)^2}=\sqrt{90}=3 \sqrt{10}\\ \therefore\quad & B D \cdot A C=30 \sqrt{10} \\ & A B \cdot C D=10 \sqrt{10} \\ & B C \cdot A D=20 \sqrt{10} \\ \therefore\quad & A B \cdot C D+B C \cdot A D=30 \sqrt{10} \\ \therefore\quad & B D \cdot A C=A B \cdot C D+B C \cdot A D \end{aligned} \(\therefore\quad A B C D\) is a cycic quadrilateral. |

