Question 1
(a) Find the first four terms, in ascending powers of $x$, of the binomial expansion of
$\begin{aligned}
&\\
(1+8 x)^{\frac{1}{2}}\\\\
\end{aligned}$
giving each term in simplest form.
(3)
(b) Explain how you could use $x=\dfrac{1}{32}$ in the expansion to find an
approximation for $\sqrt{5}$ There is no need to carry out the calculation.
(2)
Question 2
By taking logarithms of both sides, solve the equation
$\begin{aligned}
&\\
4^{3 p-1}=5^{210}\\\\
\end{aligned}$
giving the value of $p$ to one decimal place.
(3)
Question 3
Relative to a fixed origin $O$
- point $A$ has position vector $2 \mathbf{i}+5 \mathbf{j}-6 \mathbf{k}$
- point $B$ has position vector $3 \mathbf{i}-3 \mathbf{j}-4 \mathbf{k}$
- point $C$ has position vector $2 \mathbf{i}-16 \mathbf{j}+4 \mathbf{k}$
(b) Show that quadrilateral $O A B C$ is a trapezium, giving reasonsfor your answer. (2)
Question 4
The function $\mathrm{f}$ is defined by
$\begin{aligned}
&\\
f(x)=\frac{3 x-7}{x-2} \quad x \in \mathbb{R}, x \neq 2
\end{aligned}$
(a) Find $f^{-1}(7)$
(2)
(b) Show that $ff(x)=\dfrac{a x+b}{x-3}$ where $a$ and $b$ are
integers to be found.
(3)
Question 5
A car has six forward gears. The fastest speed of the car
- in $1^{\text {st }}$ gear is $28 \mathrm{~km} \mathrm{~h}^{-1}$
- in $6^{\text {th }}$ gear is $115 \mathrm{~km} \mathrm{~h}^{-1}$
(a) find the fastest speed of the car in $3^{\mathrm{rd}}$ gear. (3)
Given that the fastest speed of the car in successive gears is modelled by a geometric sequence,
(b) find the fastest speed of the car in $5^{\text {th }}$ gear. (3)
Question 6
(a) Express $\sin x+2 \cos x$ in the form $R \sin (x+\alpha)$ where $R$ and $\alpha$ are constants,
$R>0$ and $0< \alpha<\dfrac{\pi}{2}.$
Give the exact value of $R$ and give the value of $\alpha$ in radians to 3 decimal places.
(3)
The temperature, $\theta^{\circ} \mathrm{C}$, inside a room on a given day is modelled by the equation
| $\theta=5+\sin \left(\dfrac{\pi t}{12}-3\right)+2 \cos \left(\dfrac{\pi t}{12}-3\right) \quad 0 \leq t<24 $ |
|---|
where $t$ is the number of hours after midnight.
Using the equation of the model and your answer to part (a),
(b) deduce the maximum temperature of the room during this day,
(1)
(c) find the time of day when the maximum temperature occurs, giving your answer to the nearest minute.
(3)
Question 7
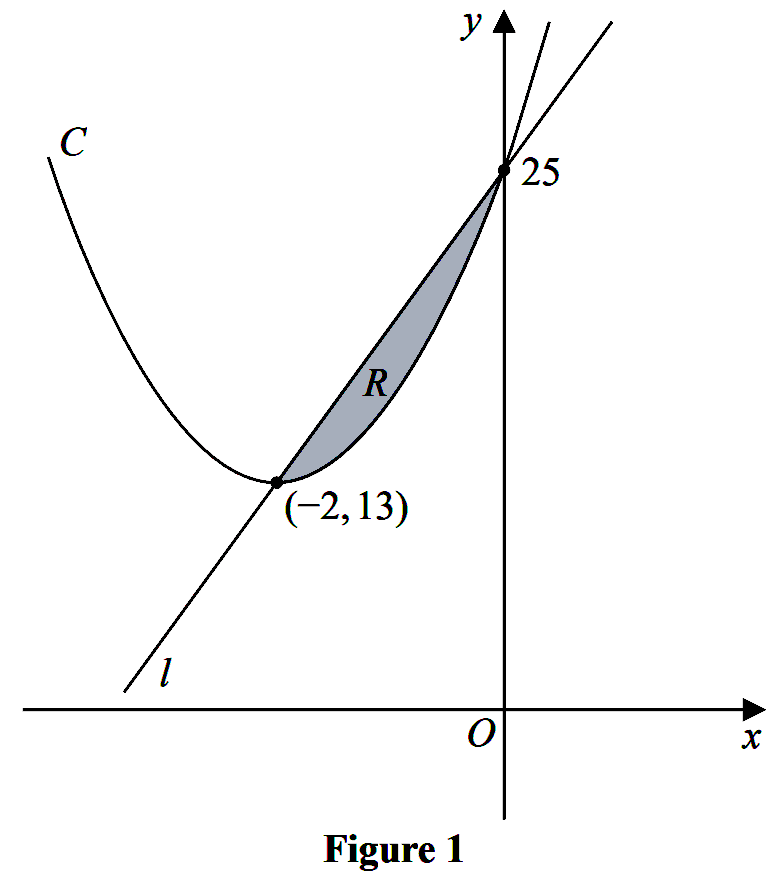
Figure 1 shows a sketch of a curve $C$ with equation $y=f(x)$ and a straight line $l$.
The curve $C$ meets $l$ at the points $(-2,13)$ and $(0,25)$ as shown.
The shaded region $R$ is bounded by $C$ and $l$ as shown in Figure 1 .
Given that
- $f(x)$ is a quadratic function in $x$
- $(-2,13)$ is the minimum turning point of $y=f(x)$
use inequalities to define $R$. (3)
Question 8
A new smartphone was released by a company.
The company monitored the total number of phones sold, $n$, at time $t$ days after the phone was released.
The company observed that, during this time, the rate of increase of $n$ was proportional to $n$.
Use this information to write down a suitable equation for $n$ in terms of $t$.
(You do not need to evaluate any unknown constants in your equation.)
(2)
Question 9
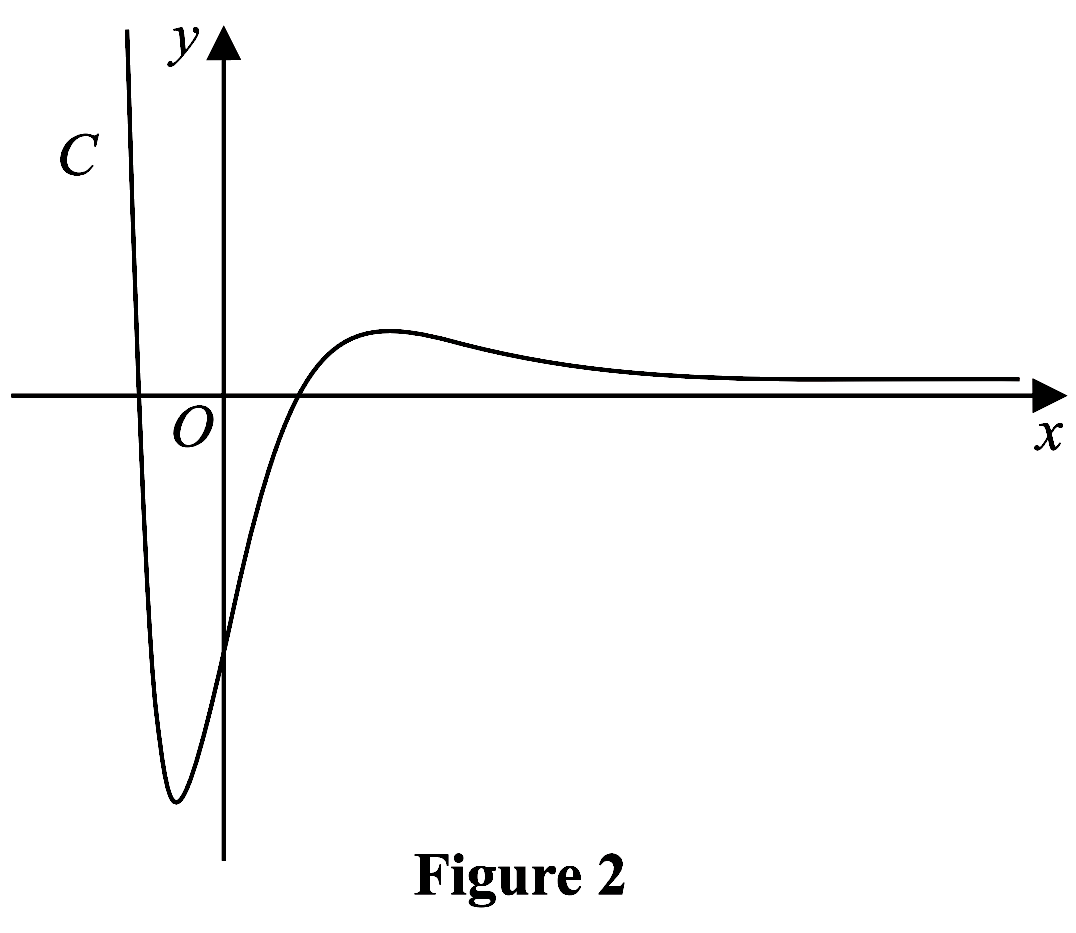
Figure 2 shows a sketch of the curve $C$ with equation $y=\mathrm{f}(x)$ where
$\begin{aligned}
&\\
f(x)=4\left(x^{2}-2\right) e^{-2 x} \quad x \in \mathbb{R}\\\\
\end{aligned}$
(a) Show that $f^{\prime}(x)=8\left(2+x-x^{2}\right)e^{-2 x}$.
(3)
(b) Hence find, in simplest form, the exact coordinates of the stationary
points of $C$.
(3)
The function $g$ and the function $h$ are defined by
$\begin{aligned}
&\\
g(x)&=2 f(x) \quad x \in \mathbb{R} \\\\
h(x)&=2 f(x)-3 \quad x \geq 0\\\\
\end{aligned}$
(c) Find
(i) the range of $g$.
(ii) the range of $h$.
(2)
Question 10
(a) (a) Use the substitution $x=u^{2}+1$ to show that
$\displaystyle\int_{5}^{10} \frac{3 ~dx}{(x-1)(3+2 \sqrt{x-1})}=\int_{p}^{q} \frac{6 ~du}{u(3+2 u)}$
(b) Hence, using algebraic integration, show that
| $\displaystyle\int_{5}^{10} \frac{3 ~dx}{(x-1)(3+2 \sqrt{x-1})}=\ln a$ |
|---|
where $a$ is a rational constant to be found. (6)
Question 11
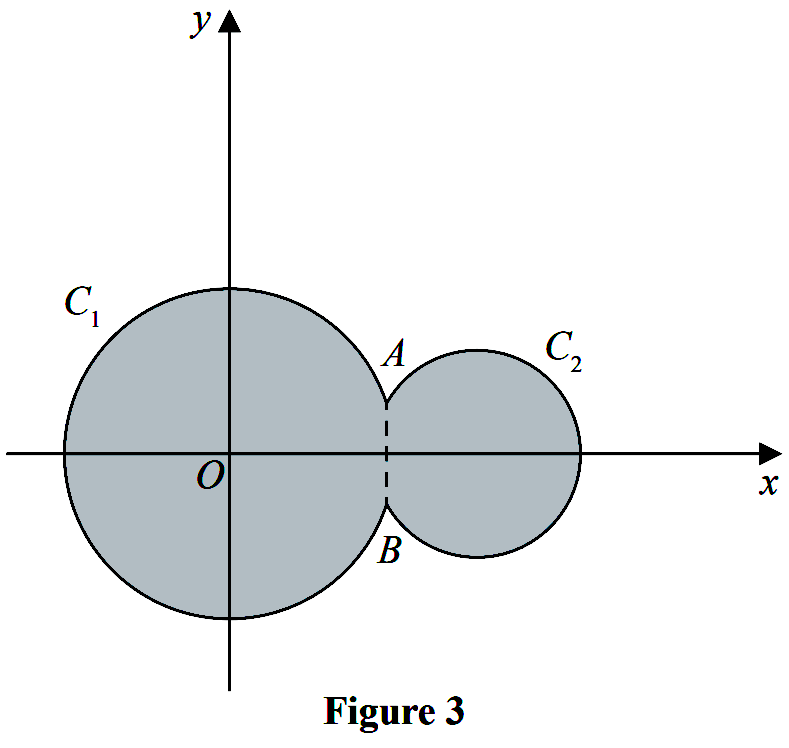
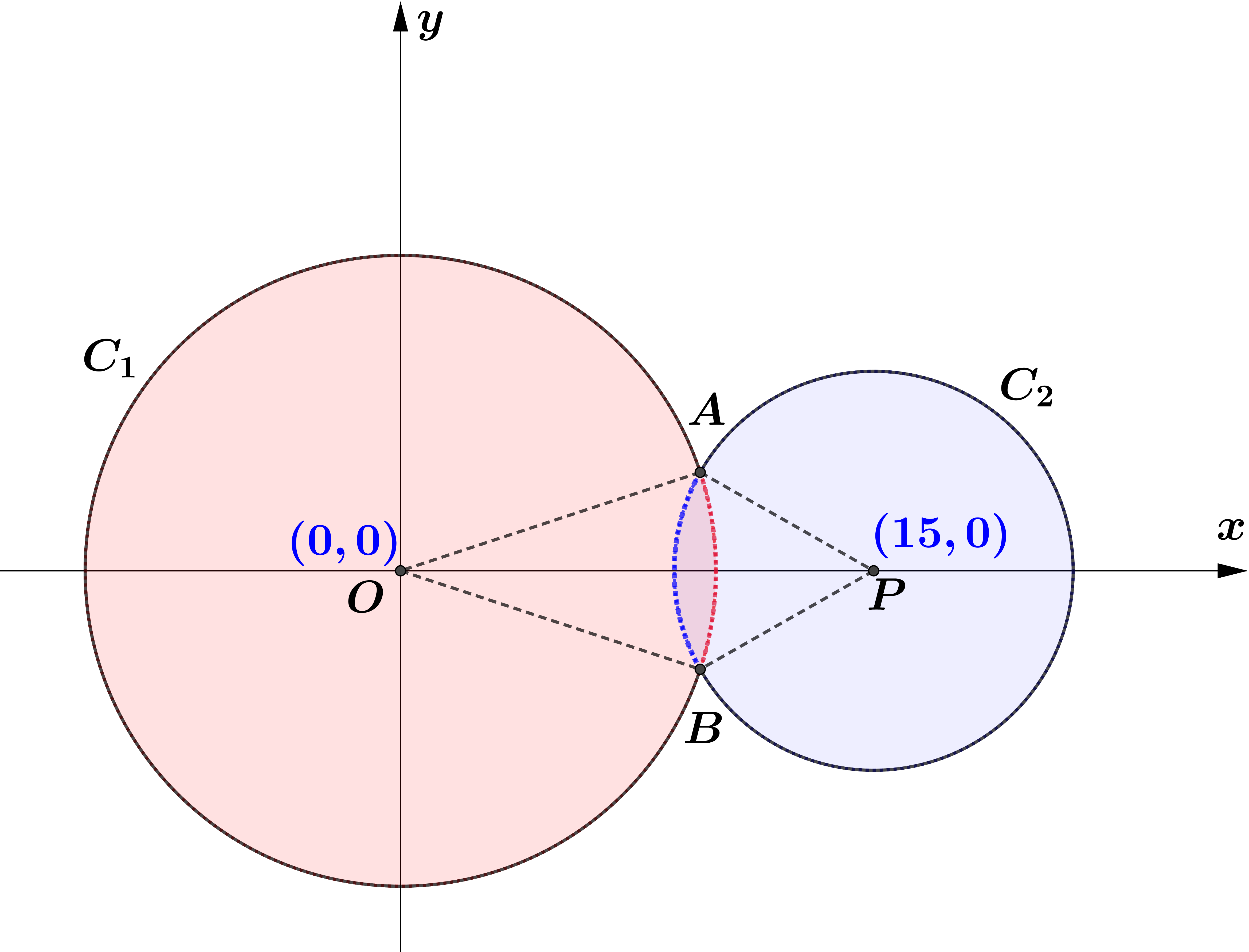
Circle $C_{1}$ has equation $x^{2}+y^{2}=100$.
Circle $C_{2}$ has equation $(x-15)^{2}+y^{2}=40$.
The circles meet at points $A$ and $B$ as shown in Figure 3 .
(a) Show that angle $A O B=0.635$ radians to 3 significant figures,
where $O$ is the origin.
(4)
The region shown shaded in Figure 3 is bounded by $C_{1}$ and $C_{2}$
(b) Find the perimeter of the shaded region, giving your answer to one decimal place.
(4)
Question 12
In this question you must show all stages of your working.
Solutions relying entirely on calculator technology are not acceptable.
(a) Show that
$\operatorname{cosec} \theta-\sin \theta \equiv \cos \theta \cot \theta \quad \theta \neq(180 n)^{\circ} \quad n \in \mathbb{Z}$
| $\operatorname{cosec} x-\sin x=\cos x \cot \left(3 x-50^{\circ}\right)$ |
|---|
Question 13
A sequence of numbers $a_{1}, a_{2}, a_{3}, \ldots$ is defined by
$\begin{aligned}
&\\
a_{n+1}=\frac{k\left(a_{n}+2\right)}{a_{n}} \quad n \in \mathbb{N}
\end{aligned}$
where $k$ is a constant.
Given that
- the sequence is a periodic sequence of order $3$.
- $a_{1}=2$
$\begin{aligned} &\\ k^{2}+k-2=0\\\\ \end{aligned}$ (3)
(b) For this sequence explain why $k \neq 1$. (2)
(c) Find the value of
$\begin{aligned} &\\ \displaystyle\sum_{r=1}^{80} a_{r} \end{aligned}$ (3)
Question 14
A large spherical balloon is deflating.
At time $t$ seconds the balloon has radius $r \mathrm{~cm}$ and volume $V \mathrm{~cm}^{3}$
The volume of the balloon is modelled as decreasing at a constant rate.
(a) Using this model, show that
$\begin{aligned}
&\\
\frac{dr}{dt}=-\frac{k}{r^{2}}\\\\
\end{aligned}$
where $k$ is a positive constant.
(3)
Given that
(b) solve the differential equation to find a complete equation linking
$r$ and $t$.
(2)
(c) Find the limitation on the values of $t$ for which the equation in part (b)
is valid.
(2)
Question 15
The curve $C$ has equation
$\begin{aligned}
&\\
x^{2} \tan y=9 \quad 0<y<\frac{\pi}{2}\\\\
\end{aligned}$
(a) Show that
$\begin{aligned}
&\\
\frac{dy}{dx}=\frac{-18 x}{x^{4}+81}\\\\
\end{aligned}$
(4)
(b) Prove that $C$ has a point of inflection at $x=\sqrt[4]{27}$
(3)
Question 16
Prove by contradiction that there are no positive integers $p$ and $q$ such that
$\begin{aligned}
&\\
4 p^{2}-q^{2}=25
\end{aligned}$
(4)