May-June-21-CIE-9709-11 : AS and A Level - Problems and Solutions

2021 (May-June) CIE (9709-Pure Mathematics 1), Paper 1/11 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။

1. The equation of a curve is such that $\dfrac{d y}{d x}=\dfrac{3}{x^{4}}+32 x^{3}$. It is given that the curve passes through the point $\left(\dfrac{1}{2}, 4\right)$. Find the equation of the curve. [4]






$\begin{aligned} \frac{d y}{d x} &=\frac{3}{x^{4}}+32 x^{3} \\\\ y &=\int\left(\frac{3}{x^{4}}+32 x^{3}\right) d x \\\\ &=3 \int x^{-4} d x+32 \int x^{3} d x \\\\ &=-\frac{1}{x^{3}}+8 x^{4}+C\\\\ \end{aligned}$ The curve passes through the point $\left(\dfrac{1}{2}, 4\right)$. $\begin{aligned} &\\ \therefore\ 4&=-\frac{1}{\left(\frac{1}{2}\right)^{3}}+8\left(\frac{1}{2}\right)^{4}+c \\\\ &4=-8+\frac{1}{2}+c \\\\ &c=\frac{23}{2} \\\\ &y=-\frac{1}{x^{3}}+8 x^{4}+\frac{23}{2} \end{aligned}$




2. The sum of the first $20$ terms of an arithmetic progression is $405$ and the sum of the first $40$ terms is $1410$ .Find the $60^{\text{th}}$ term of the progression. [5]






Let the first term be $a$, the common difference be $d$ and the sum to first $n$ terms be $S_n$ of given A.P. $\begin{aligned} &\\ \therefore\ S_{20} &=405 \\\\ \frac{20}{2}\{2 a+19 d\} &=405 \\\\ 2 a+19 d &=40.5 \ldots (1)\\\\ S_{40} &=1410 \\\\ \frac{40}{2}\{2 a+39 d\} &=1410 \\\\ 2 a+39 d &=70.5 \ldots (2)\\\\ \end{aligned}$ Solving equation $(1)$ and (2), $\begin{aligned} &\\ a=6, d &=\frac{3}{2} \\\\ \therefore\ 60^{\text {th }} \text { term } &=a+59 d \\\\ &=6+59 \times \frac{3}{2} \\\\ &=94.5 \end{aligned}$




3. (a) Find the first three terms in the expansion of $(3 - 2x)^5$ in ascending powers of $x$. [3]
   (b) Hence find the coefficient of $x^2$ in the expansion of $(4 + x)^2(3-2x)^5$.[3] [4]






$\begin{aligned} (3-2 x)^{5}&=3^{5} 5\left(3^{4}\right)(2 x)+10\left(3^{3}\right)(2 \times)^{2}+\cdots \\\\ &=24^{3}-810 x+1080 x^{2}+\cdots \\\\ (4+x)^{2}&=16+8 x+x^{2} \\\\ (4+x)^{2}(3+2 x)^{5}&=\left(16+8 x+x^{2}\right)\left(2 y^{3}-810 x+1080 x^{2}+\cdots\right) \\\\ \therefore & \quad\text { Coefficient of } x^{2} \text { in the expansion of }(4+x)^{2}(3+2 x)^{5} \\\\ &=16(1080)-8(80)+1(243) \\\\ &=11043 \end{aligned}$





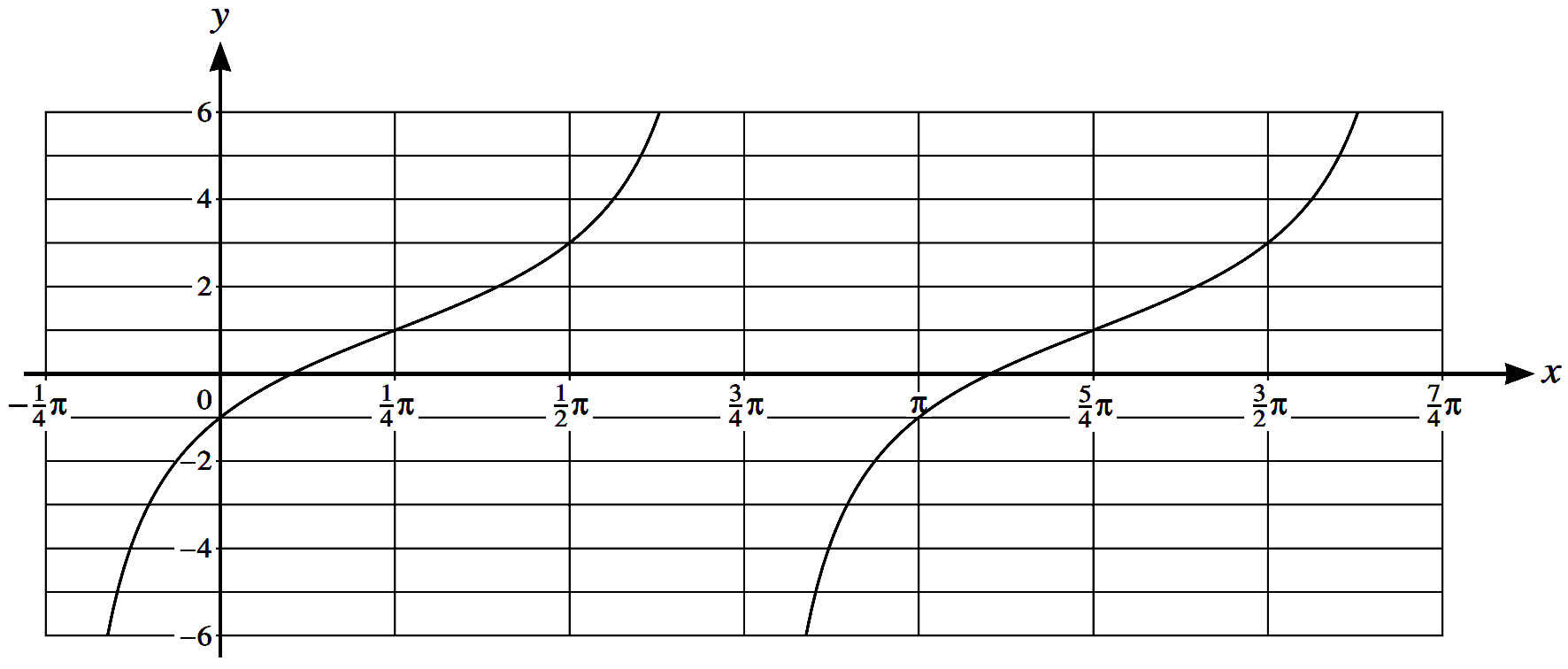
4. The diagram shows part of the graph of $y = a \tan (x - b) + c$. Given that $0 < b < \pi$, state the values of the constants $a, b$ and $c$. [4]






$y=a \tan (x-b)+c\\\\ $ The graph passes throught the points $(0,-1),\left(\dfrac{\pi}{4},+\right)$ and $\left(\dfrac{\pi}{2}, 3\right)$. $\begin{aligned} &\\ &a \tan (0-b)+c=-1\\\\ &-a \tan b+c=-1 \ldots (1)\\\\ &a \tan \left(\frac{\pi}{4}-b\right)+c=1 \ldots(2)\\\\ &a \tan \left(\frac{\pi}{2}-b\right)+c=3 \ldots(3)\\\\ &(2)-(1)\\\\ &a\left[\tan \left(\frac{\pi}{4}-b\right)+\tan b\right]=2\\\\ &(3)-(2), \\\\ &a\left[\tan \left(\frac{\pi}{2}-b\right)-\tan \left(\frac{\pi}{4}-b\right)\right]=2\\\\ &\therefore\ \tan \left(\frac{\pi}{4}-b\right)+\tan b=\tan \left(\frac{\pi}{2}-b\right)-\tan \left(\frac{\pi}{4}-b\right)\\\\ &\tan \left(\frac{\pi}{4}-b\right) =\frac{1}{2}\left[\tan \left(\frac{\pi}{2}-b\right)-\tan b\right] \\\\ &\frac{1-\tan b}{1+\tan b} =\frac{1}{2}\left[\frac{1}{\tan b}-\tan b\right] \\\\ &\frac{1-\tan b}{1+\tan b} =\frac{1-\tan ^{2} b}{2 \tan b}\\\\ &2 \tan b-2 \tan ^{2} b =1-\tan ^{2} b+\tan b-\tan ^{3} b\\\\ &\tan ^{3} b-\tan ^{2} b+\tan b-1=0 \\\\ &\tan ^{2} b(\tan b-1)+\tan b-1=0\\\\ &(\tan b-1)\left(\tan ^{2} b+1\right)=0\\\\ &\text{ For } 0 < b<\pi, \tan ^{2} b+1>0\\\\ &\therefore \ \tan b-1=0\\\\ &\tan b=1\\\\ &b=\frac{\pi}{4}\\\\ \end{aligned}$ Substituting $b=\dfrac{\pi}{4}$ in equation $(2),c=1\\\\\\\\ $ Substituting b $=\dfrac{\pi}{4}$ and $c=1$ in equation $(1)$, $\begin{aligned} &\\ &-a \tan \frac{\pi}{4}+1 =-1 \\\\ &-a+1 =-1 \\\\ &a =2 \end{aligned}$




5. The fifth, sixth and seventh terms of a geometric progression are $8k$, $-12$ and $2k$ respectively.Given that $k$ is negative, find the sum to infinity of the progression. [4]
   






$\begin{aligned} \text{In a G . P,}& \\\\ u_{5} & =8 k \\\\ u_{6} & =-12 \\\\ u_{7} & =2 k \\\\ \therefore\ \frac{-12}{8 k} & =\frac{2 k}{-12} \\\\ k^{2} & =9 \\\\ k & =-3(\because k<0)\\\\ \therefore\ u_{5} & =-24 \\\\ u_{6} &=-12 \\\\ u_{7} &=-6 \\\\ r &=\frac{-6}{-12} \\\\ &=\frac{1}{2} \\\\ a r &=-24 \\\\ a\left(\frac{1}{2}\right)^{4} &=-24\\\\ a&=-384\\\\ \end{aligned}$ Let the sum to infinity be $S$, then $\begin{aligned} &\\ S &=\frac{a}{1-r} \\\\ &=\frac{-384}{1-\frac{1}{2}} \\\\ &=-768 \end{aligned}$




6. The equation of a curve is $y = (2k - 3)x^2 - kx - (k - 2)$, where $k$ is a constant. The line $y = 3x - 4$ is a tangent to the curve. Find the value of $k$. [5]
   






$\begin{aligned} \text{ Curve }: y&=(2 k-3) x^{2}-k x-(k-2)\\\\ \text{ Line }: y&=3 x-4\\\\ \end{aligned}$ At the point of intersection line and curve, $\begin{aligned} &(2 k-3) x^{2}-k x-(k-2)=3 x-4 \\\\ \therefore\ &(2 k-3) x^{2}-(k+3) x+6-k=0\\\\ \end{aligned}$ Since the line is tangent to the curve, $\begin{aligned} &\\ &\text{ Discriminant } =0\\\\ &(k+3)^{2}-4(2 k-3)(6-k)=0\\\\ &k^{2}+6 k+9-4\left(-2 k^{2}+15 k-18\right)=0 \\\\ &k^{2}+6 k+9+8 k^{2}-60 k+72=0 \\\\ &9 k^{2}-54 k+81=0 \\\\ &k^{2}-6 k+9=0 \\\\ &(k-3)^{2}=0 \\\\ &k=3 \end{aligned}$




7. (a) Prove the identity $\dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta} \equiv 1-\tan ^{2} \theta$. [2]
   (b) Hence solve the equation $\dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta}=2 \tan ^{4} \theta$ for $0^{\circ} \leq \theta \leq 180^{\circ}$. [3]
   






$\begin{aligned} \dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta} &=\dfrac{\cos ^{2} \theta-\sin ^{2} \theta}{\cos ^{2} \theta} \\\\ &=\dfrac{\cos ^{2} \theta}{\cos ^{2} \theta}-\dfrac{\sin ^{2} \theta}{\cos ^{2} \theta} \\\\ &=1-\tan ^{2} \theta\\\\ \end{aligned}$ $\begin{aligned} &\dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta}=2 \tan ^{4} \theta \\\\ &1-\tan ^{2} \theta=2 \tan ^{4} \theta \\\\ &2 \tan ^{4} \theta+\tan ^{2} \theta-1=0 \\\\ &\left(2 \tan ^{2} \theta-1\right)\left(\tan ^{2} \theta+1\right)=0 \\\\ &\sin \cot \tan ^{2} \theta+1>0 \\\\ & 2 \tan ^{2} \theta-1=0 \\\\ &\tan ^{2} \theta=\dfrac{1}{2} \\\\ &\tan \theta=-\dfrac{1}{\sqrt{2}} \text { or } \tan \theta=\dfrac{1}{\sqrt{2}} \\\\ &\theta=144.7^{\circ} \text { or } \theta=35.3^{\circ} \end{aligned}$





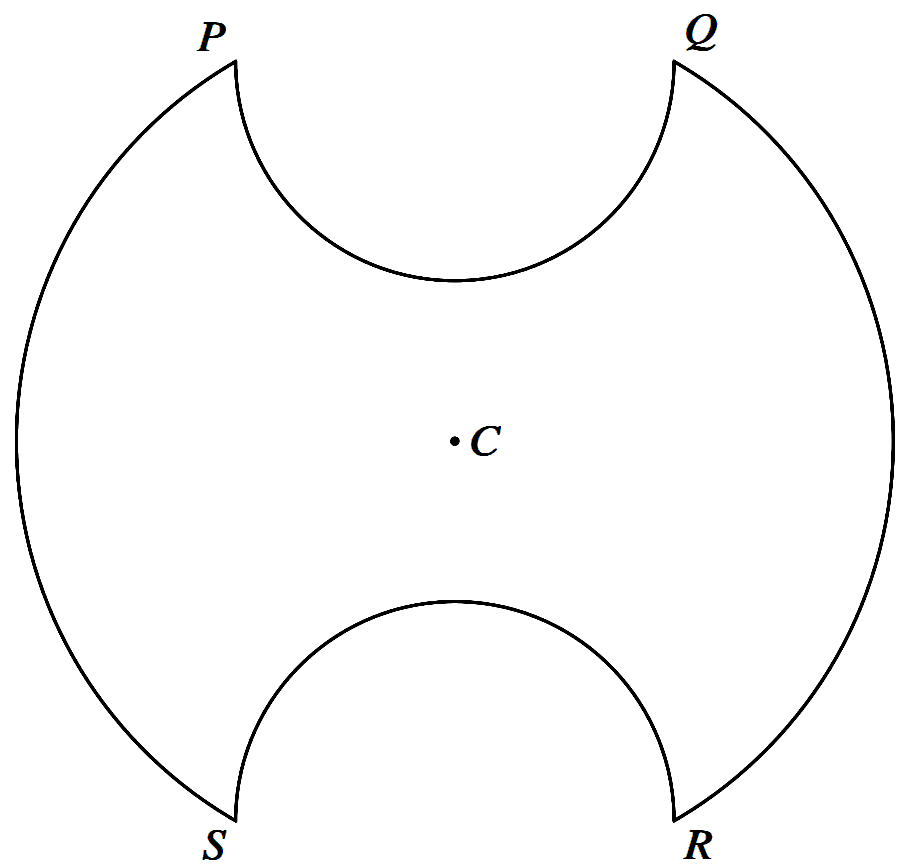
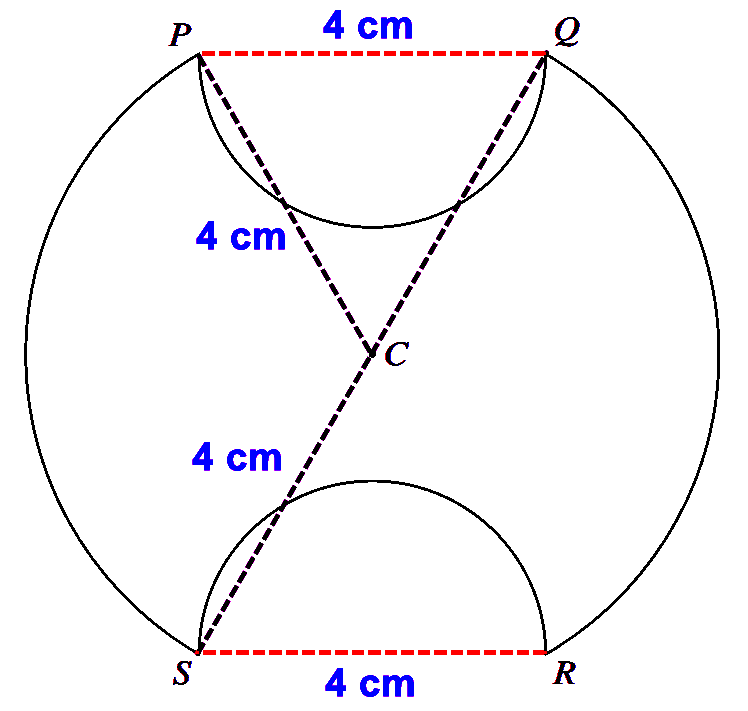
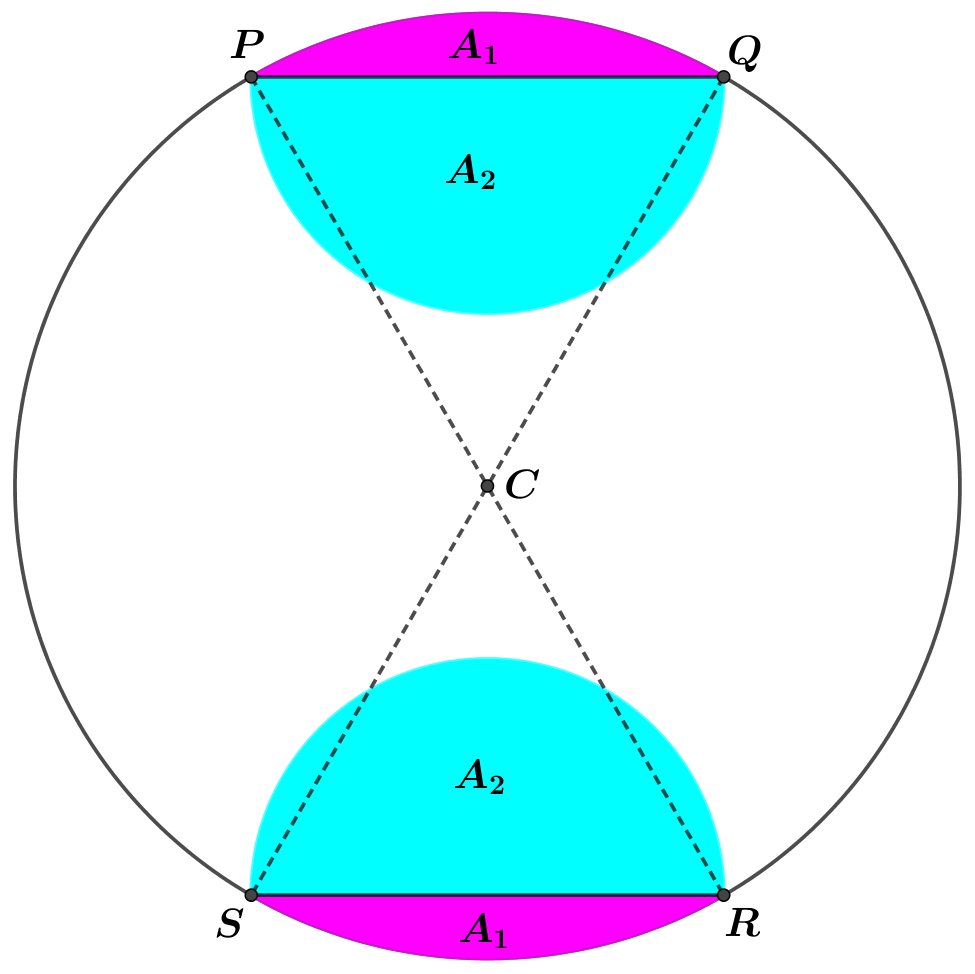
8. The diagram shows a symmetrical metal plate. The plate is made by removing two identical piecesfrom a circular disc with centre $C$. The boundary of the plate consists of two arcs $PS$ and $QR$ of the original circle and two semicircles with $PQ$ and $RS$ as diameters. The radius of the circle with centre $C$ is $4$ cm, and $PQ = RS = 4$ cm also.
   (a) Show that angle $PCS = \dfrac{2}{3}\pi$ radians. [2]
   (b) Find the exact perimeter of the plate. [3]
   (c) Show that the area of the plate is $\left(\dfrac{20}{3} \pi+8 \sqrt{3}\right) \mathrm{cm}^{2}$. [5]






$\text{ (a) } \quad \triangle P C Q$ is equilateral. $\begin{aligned} &\\ \therefore \quad \angle P C Q &=\frac{\pi}{3} \\\\ \angle P C S &=\pi-\frac{\pi}{3} \\\\ &=\frac{2 \pi}{3} \\\\ \end{aligned}$ $\begin{aligned} \text{ (b) } \quad & \qquad \text{ arc length of } PS \\\\ &= \text{ arc length of } SR \\\\ &= 4 \times \frac{2 \pi}{3} \\\\ &= \frac{8 \pi}{3} \mathrm{~cm}\\\\ \end{aligned}$ $\begin{aligned} &\quad \text{ arc length of semicircle } PQ \\\\ &= \text{ arc length of semicircle } SR\\\\ &=\pi \times \frac{4}{2} \\\\ &=2 \pi\ \mathrm{cm}\\\\ &\quad \text{ perimeter of metal plate }\\\\ &=2\left(\frac{8 \pi}{3}+2 \pi\right) \\\\ &=\frac{28 \pi}{3} \mathrm{~cm}\\\\ \end{aligned}$ $\begin{aligned} \text{ (c) } \quad A_{1} &= \text{ area of sector - area of triangle}\\\\ &=\frac{1}{2} \times 4^{2} \times \frac{\pi}{3}-\frac{\sqrt{3}}{4} \times 4^{2} \\\\ &=\frac{8 \pi}{3}-4 \sqrt{3} \\\\ A_{2} &=\text { area of semicircle } \\\\ &=2 \pi\\\\ &\quad\text{ area of metal plate }\\\\ &=\text { area of } \odot C-2\left(A_{1}+A_{2}\right) \\\\ &=\pi \times 4^{2}-2\left(\frac{8 \pi}{3}-4 \sqrt{3}+2 \pi\right) \\\\ &=\left(\frac{20 \pi}{3}+8 \sqrt{3}\right) \mathrm{cm}^{2} \end{aligned}$




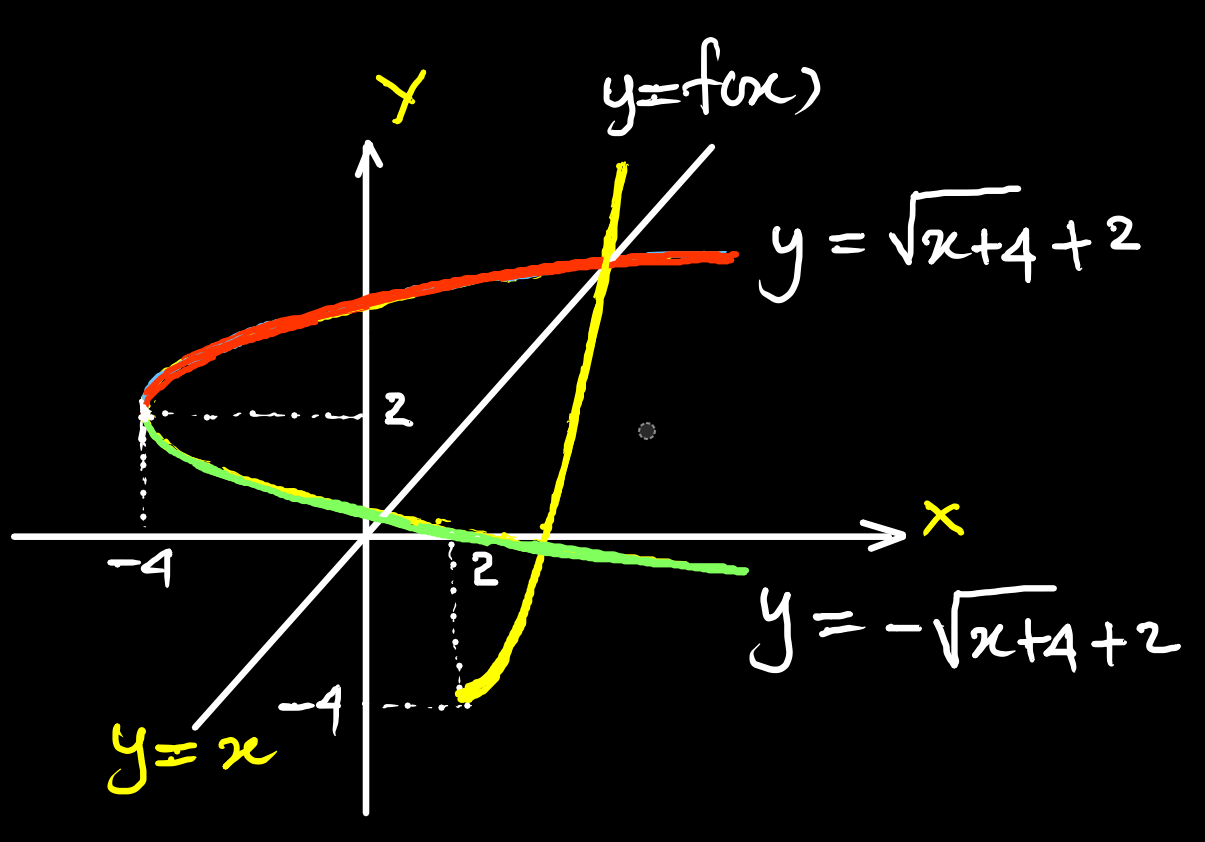
9. Functions $f$ and $g$ are defined as follows:
   $\begin{aligned} &\\ &f(x)=(x-2)^{2}-4 \text { for } x \geq 2 \\\\ &g(x)=a x+2 \text { for } x \in \mathbb{R}\\\\ \end{aligned}$
   where $a$ is a constant.
   (a) State the range of $f$. [1]
   (b) Find $f^{-1}(x)$. [2]
   (c) Given that $a = -\dfrac{5}{3}$, solve the equation $f(x) = g(x)$. [3]
   (d) Given instead that $ggf^{-1}(12) = 62$, find the possible values of $a$. [5]






$\begin{aligned} f(x)=(x-2)^{2}-4 , x \geq 2\\\\ g(x)=a x+2, x \in R\\\\ \end{aligned}$ $\text{ (a) }\ $ range of $f=\{y \mid y \geq-4, y \in R\}$ $\begin{aligned} &\\ \text{ (b) } \text{ Let } f^{-1}(x)&=y\\\\ f(y) &=x \\\\ (y-2)^{2}-4 &=x \\\\ (y-2)^{2} &=x+4 \\\\ y &=\pm \sqrt{x+4}+2\\\\ \end{aligned}$ Since $f^{-1}(x)$ is the reflection of $f(x)$ in the line $y=x$, $f^{-1}(x)=\sqrt{x+4}+2$. $\begin{aligned} &\\ \text{ (c) }\hspace{1cm}\text { When } a &=-\frac{5}{3},\\\\ g(x) &=-\frac{5}{3} x+2 \\\\ f(x) &=g(x) \\\\ (x-2)^{2}-4 &=-\frac{5}{3} x+2 \\\\ x^{2}-4 x &=-\frac{5}{3} x+2 \\\\ 3 x^{2}-12 x &=-5 x+6 \\\\ 3 x^{2}-7 x-6 &=0 \\\\ (3 x+2)(x-3) &=0 \\\\ x=-\frac{2}{3} \text { or } x &=3\\\\ \end{aligned}$ $\begin{aligned} \text{ (d) }\hspace{1cm} g g f^{-1}(12) &=62 \\\\ g\left(g\left(f^{-1}(12)\right)\right) &=62 \\\\ g(g(\sqrt{12+4}+2)) &=62 \\\\ g(g(6)) &=62 \\\\ g(6 a+2) &=62 \\\\ a(6 a+2)+2 &=62 \\\\ 6 a^{2}+2 a-60 &=0 \\\\ 3 a^{2}+a-30 &=0 \\\\ (3 a+10)(a-3) &=0\\\\ \therefore\ a=-\frac{10}{3} \text { or } a &=3 \end{aligned}$




10. The equation of a circle is $x^2 + y^2 - 4x + 6y - 77 = 0$.
    (a) Find the $x$-coordinates of the points $A$ and $B$ where the circle intersects the $x$-axis. [2]
    (b) Find the point of intersection of the tangents to the circle at $A$ and $B$.
    [6]






$\begin{aligned} & x^{2}+y^{2}-4 x+6 y-77=0 \\\\ & x^{2}+y^{2}-4 x+6 y=77 \\\\ & x^{2}-4 x+4+y^{2}+6 y+9=77+13 \\\\ &(x-2)^{2}+(y+3)^{2}=90\\\\ \end{aligned}$ Let $O$ be the centere of tre circle. $\therefore$ The coordinates of the point $O$ is $(2,-3)\\\\ $. When the circle interseets $x$-axis, $y=0\\\\ $. $\begin{aligned} &\\ \therefore\ &(x-2)^{2}+9=90 \\\\ &(x-2)^{2}=81 \\\\ & x-2=\pm 9 \\\\ \therefore\ & x=2-9 \text { or } x=2+9 \\\\ \therefore\ & x=-7 \text { or } x=11\\\\ \end{aligned}$ $\therefore$ The circle intersects $x$-axis at $A(-7,0)$ and $B(11, 0).\\\\ $ Gradient of $A O=\dfrac{-3}{2+7}=-\dfrac{1}{3}\\\\ $ $\therefore$ Gradient of tangent at $A=3\\\\ $ Equation of tangent at $A$ is $y=3(x+7)\\\\ $ Gradient of $B O=\dfrac{-3}{2-11}=\dfrac{1}{3}\\\\ $ Gradient of tangent at $B=-3.\\\\ $ Equation of tangent at $B$ is $y=-3(x-11)\\\\ $ At the point of intersection of two tangents, $\begin{aligned} &\\ 3(x+7) &=-3(x-11) \\\\ x+7 &=-x+11 \\\\ x &=2 \\\\ \therefore\ y &=27\\\\ \end{aligned}$ $\therefore\ $ The point of intersection of the two tangents is $(2,27).$




11. The equation of a curve is $y=2 \sqrt{3 x+4}-x$.
    (a) Find the equation of the normal to the curve at the point $(4,4)$, giving your answer in the form $y=m x+c$. [5]
    (b) Find the coordinates of the stationary point. [3]
    (c) Determine the nature of the stationary point. [2]
    (d) Find the exact area of the region bounded by the curve, the x-axis and the lines $x = 0$ and $x = 4$. [4]






$\text{ (a) }$ Curve: $y=2 \sqrt{3 x+4}-x$ $\begin{aligned} &\\ \dfrac{d y}{d x} &=\dfrac{2}{2 \sqrt{3 x+4}} \dfrac{d}{d x}(3 x+4)-1 \\\\ &=\dfrac{3}{\sqrt{3 x+4}}-1 \end{aligned}$ At the point $(4,4)$, $\begin{aligned} &\\ \dfrac{d y}{d x} &=\dfrac{3}{\sqrt{12+4}}-1 \\\\ &=\dfrac{3}{4}-1=-\dfrac{1}{4}\\\\ \end{aligned}$ $\therefore$ Gradient of normal at $(4,4)$ is 4. Equation of normal to the curve at $(4,4)$ is $\begin{aligned} &\\ y-4 &=4(x-4) \\\\ y &=4 x-12\\\\ \text{ (b) } \quad \text{ When } \dfrac{d y}{d x}&=0\\\\ \dfrac{3}{\sqrt{3 x+4}}-1&=0\\\\ \sqrt{3 x+4} &=3 \\\\ 3 x+4 &=9 \\\\ x &=\dfrac{5}{3} \\\\ \text { When } x &=\dfrac{5}{3} \\\\ y &=2 \sqrt{3\left(\dfrac{5}{3}\right)+4}-\dfrac{5}{3} \\\\ &=\dfrac{13}{3}\\\\ \end{aligned}$ $\therefore$ The stationary point is $\left(\dfrac{5}{3}, \dfrac{13}{3}\right)$. $\begin{aligned} &\\ \text{ (c) } \quad \dfrac{d^{2} y}{d x^{2}} &=\dfrac{d}{d x}\left(\dfrac{3}{\sqrt{3 x+4}}-1\right) \\\\ &=\dfrac{d}{d x}\left(3(3 x+4)^{-1/2}-1\right) \\\\ &=-\dfrac{9}{2(3 x+4)^{3 / 2}}\\\\ \text { When } x&=\dfrac{5}{3}\\\\ \dfrac{d^{2} y}{d x^{2}}&=\dfrac{-9}{2 \sqrt{3\left(\dfrac{5}{3}\right)+4}}<0\\\\ \end{aligned}$ $\therefore\left(\dfrac{5}{3}, \dfrac{13}{3}\right)$ is a maximum. $\begin{aligned} &\\ \text{ (d) }\quad\text { required area } &=\displaystyle\int_{0}^{4}\left[2(3 x+4)^{1/2}-x\right] d x \\\\ &=2 \displaystyle\int_{0}^{4}(3 x+4)^{1 / 2} d x-\displaystyle\int_{0}^{4} x d x \\\\ &=\dfrac{2}{3} \displaystyle\int_{0}^{4}(3 x+4)^{1/2} d(3 x+4)-\displaystyle\int_{0}^{4} x d x \\\\ &\left.=\dfrac{4}{9}\left[(3 x+4)^{3 / 2}\right]_{0}^{4}-\dfrac{x^{2}}{2}\right]_{0}^{4} \\\\ &=\dfrac{4}{9}[64-8]-\dfrac{16}{2}\\\\ &=\dfrac{152}{9} \end{aligned}$

စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!