-
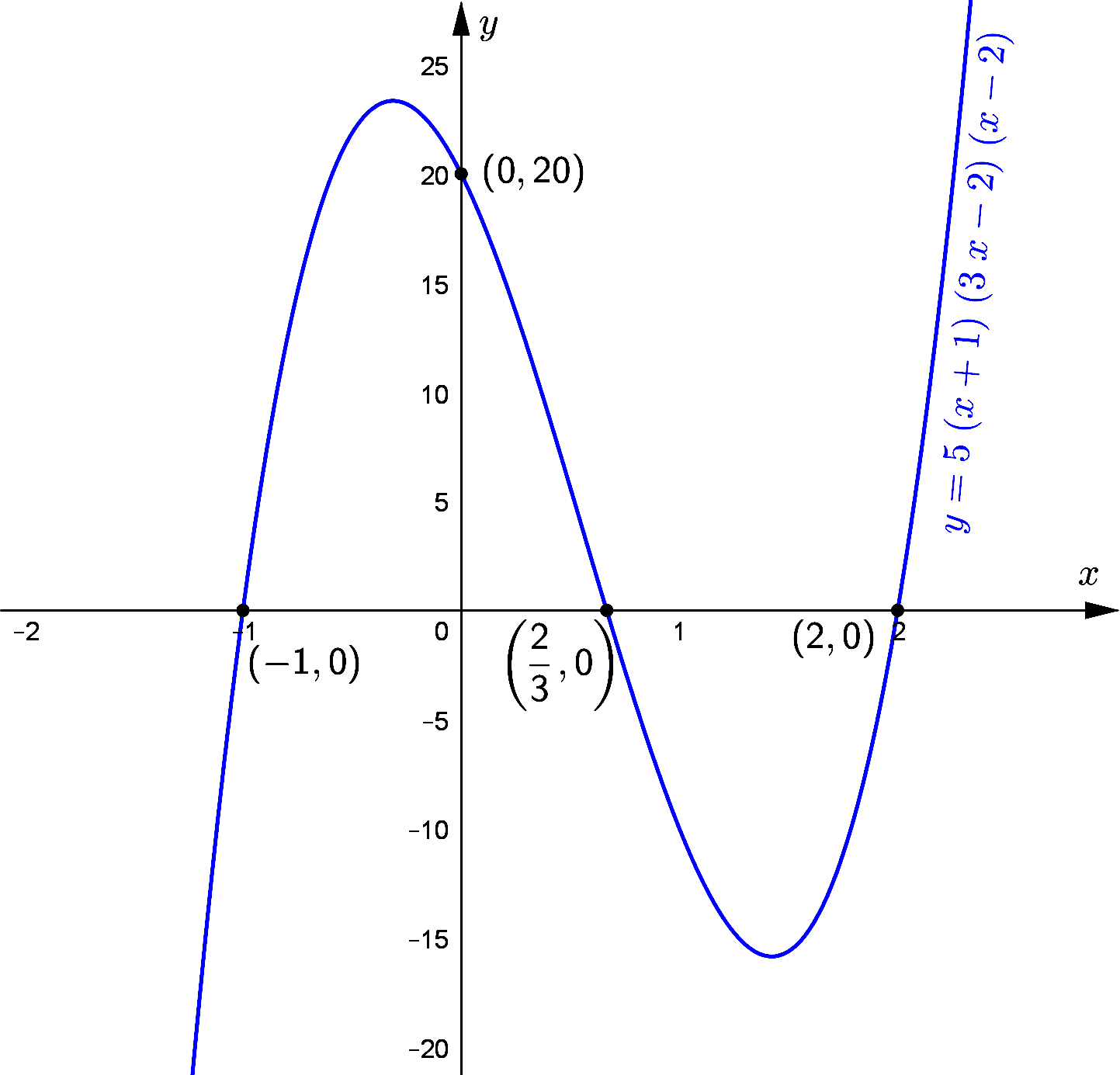
(a) On the axes, sketch the graph of $y = 5(x+1)(3x-2)(x-2)$, stating the intercepts with the coordinate axes. [3]
(b) Hence find the values of x for which $5(x+1)(3x-2)(x-2)>0$ . [2] -
Find $\displaystyle\int_{3}^{5}\left(\dfrac{1}{x-1}-\dfrac{1}{(x-1)^{2}}\right) \mathrm{d} x$, giving your answer in the form $a+\ln b$, where $a$ and $b$ are rational numbers. [5]
-
The polynomial $p(x)=a x^{3}-9 x^{2}+b x-6$, where $a$ and $b$ are constants, has a factor of $x-2 .$ The polynomial has a remainder of $66$ when divided by $x-3$.
(a) Find the value of $a$ and of $b$. [4]
(b) Using your values of $a$ and $b$, show that $p(x)=(x-2)q(x)$ , where $q(x)$ is a quadratic factor to be found. [2]
(c) Hence show that the equation $p(x) = 0$ has only one real solution. [2] -
The first 3 terms in the expansion of $(a+x)^{3}\left(1-\dfrac{x}{3}\right)^{5}$, in ascending powers of $x$, can be written in the form $27+b x+c x^{2}$, where $a, b$ and $c$ are integers. Find the values of $a, b$ and $c$. [8]
-
The functions $f$ and $g$ are defined as follows.
$\begin{aligned} &\\ &f(x)=x^{2}+4 x \text { for } x \in \mathbb{R} \\\\ & g(x)=1+e^{2 x} \text { for } x \in \mathbb{R}\\\\ \end{aligned}$
(a) Find the range of $f$. [2]
(b) Write down the range of $g$. [1]
(c) Find the exact solution of the equation $fg(x) = 21$, giving your answer as a single logarithm. [4] -
(a) (i) Find how many different 5-digit numbers can be formed using the digits 1, 3, 5, 6, 8 and 9. No digit may be used more than once in any 5-digit number. [1]
(ii) How many of these 5-digit numbers are odd? [1]
(iii) How many of these 5-digit numbers are odd and greater than 60000? [3]
(b) Given that $45 \times{ }^{n} \mathrm{C}_{4}=(n+1) \times{ }^{n+1} \mathrm{C}_{5}$, find the value of $n$. [4] -
(a) In this question, all lengths are in metres and time, t, is in seconds.
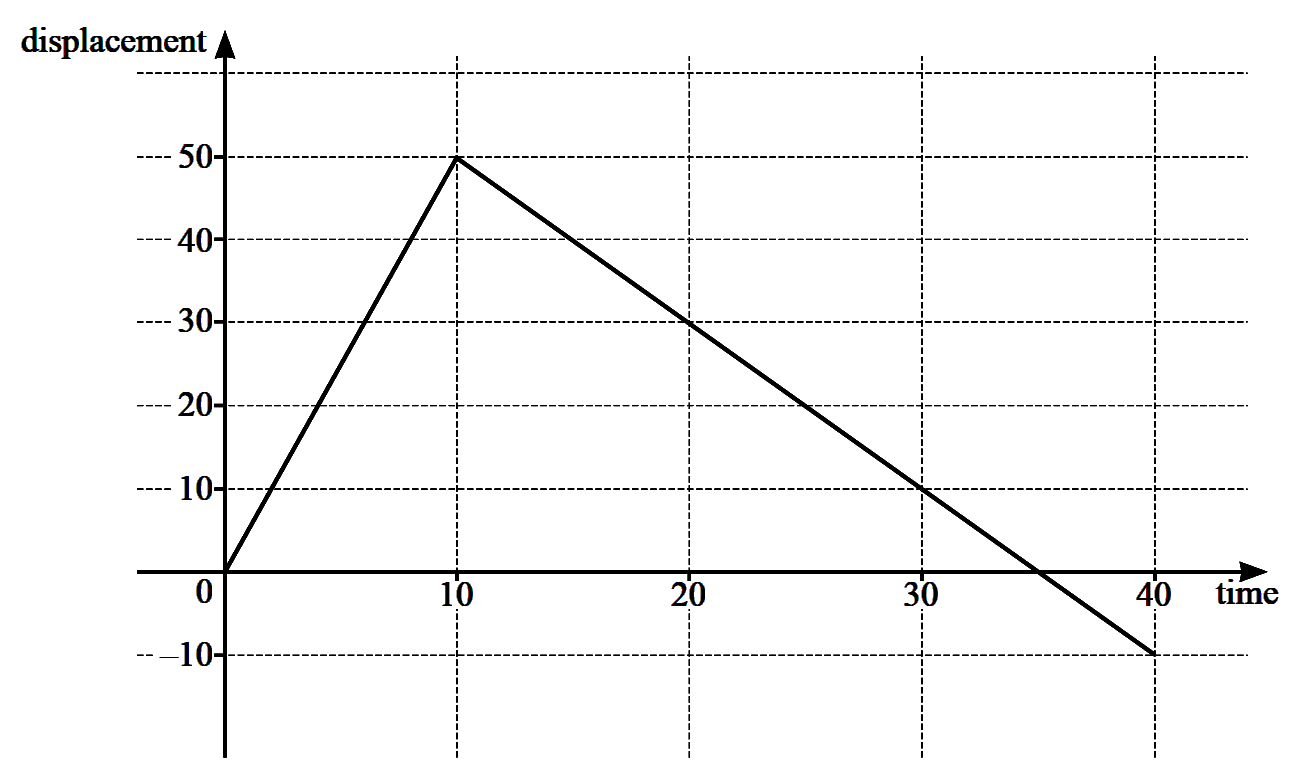
The diagram shows the displacement–time graph for a runner, for $0\le t\le 40$.
(i) Find the distance the runner has travelled when $t = 40$. [1]
(ii) On the axes, draw the corresponding velocity–time graph for the runner, for $0\le t\le 40$. [2]
(b) A particle, $P$, moves in a straight line such that its displacement from a fixed point at time $t$ is $s$. The acceleration of $P$ is given by $(2 t+4)^{-\frac{1}{2}}$, for $t>0$.
(i) Given that $P$ has a velocity of $9$ when $t=6$, find the velocity of $P$ at time $t$. [3]
(ii) Given that $s=\dfrac{1}{3}$ when $t=6$, find the displacement of $P$ at time $t$. [3] -
DO NOT USE A CALCULATOR IN THIS QUESTION.
A curve has equation $y=(2-\sqrt{3}) x^{2}+x-1$. The $x$-coordinate of a point $A$ on the curve is $\dfrac{\sqrt{3}+1}{2-\sqrt{3}}$.
(a) Show that the coordinates of $A$ can be written in the form $(p+q \sqrt{3}, r+s \sqrt{3})$, where $p, q, r$ and $s$ are integers. [5]
(b) Find the $x$-coordinate of the stationary point on the curve, giving your answer in the form $a+b \sqrt{3}$, where $a$ and $b$ are rational numbers. [3] -
(a) (i) Write $6 x y+3 y+4 x+2$ in the form $(a x+b)(c y+d)$, where $a, b, c$ and $d$ are positive integers. [1]
(ii) Hence solve the equation $6 \sin \theta \cos \theta+3 \cos \theta+4 \sin \theta+2=0$ for $0^{\circ} <\theta<360^{\circ}$.
[4]
(b) Solve the equation $\dfrac{1}{2} \sec \left(2 \phi+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{3}}$ for $-\pi<\phi<\pi$, where $\phi$ is in radians. Give your answers in terms of $\pi$. [5]
-
In this question all lengths are in centimetres.
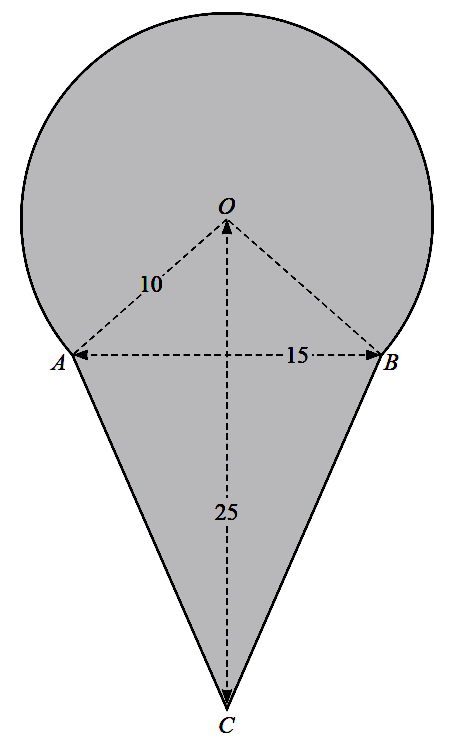
The diagram shows a shaded shape. The arc $AB$ is the major arc of a circle, centre $O$, radius $10$. The line $AB$ is of length $15$, the line $OC$ is of length $25$ and the lengths of $AC$ and $BC$ are equal.
(a) Show that the angle $AOB$ is $1.70$ radians correct to $2$ decimal places. [2]
(b) Find the perimeter of the shaded shape. [4]
(c) Find the area of the shaded shape. [5]
2021 (May-June) CIE (0606-Additional Mathematics), Paper 1 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!