-
Differentiate the following with respect to $x$.
(a) $\left(2 x^{2}+3 x\right)^{10}\\\\ $
(b) $\dfrac{1}{3-2 x}\\\\ $
(c) $\sqrt{9-x^{2}}\\\\ $
(d) $\left(x^{2}+\dfrac{3}{x}\right)^{5}\\\\ $ - Differentiate $\sqrt{x+7}\left(x^{2}+2\right)^{7}$ with respect to $x$.
- Differentiate $\dfrac{x^{2}}{\sqrt{x+1}}$ with respect to $x$.
-
Differentiate the following with respect to $x.\\\\ $
(a) $\left(2 x^{2}+3\right)^{4}\left(x^{2}-3 x\right)^{5}\\\\ $
(b) $\left(3+x^{2}\right) \sqrt{3-x^{2}}\\\\ $
(c) $\dfrac{\sqrt{x+3}}{x+1}\\\\ $
(d) $\dfrac{3 x-5}{2 x^{2}+7}\\\\ $
(e) $\dfrac{2 x-7}{\sqrt{x+7}}\\\\ $
(f) $\sqrt{\dfrac{x^{2}+1}{x^{2}-1}}\\\\ $
- Calculate the gradient of the curve $y=\dfrac{3 x^{2}-8}{5-2 x}$ at the point $(2,4)$.
- Calculate the gradient of the curve $y=x \sqrt{x+3}$. Find the coordinate of the point at which the gradient is zero.
- Find the equation of the normal to the curve $y=\dfrac{x^{2}+1}{x-1}$ at the point on the curve where $x=2$.
- Find the equation of the normal to the curve $y=\dfrac{4 x+1}{x-1}$ at the point on the curve where $y=5$.
- If $f(x)=\dfrac{k+x}{1-2 x}$ where $k$ is a constant, find $f^{\prime}(x)$ in terms of $x$ and $k$. Given that $f^{\prime}(3)=0.52$, show that $k=6$.
- Find the equation of the normal to the curve $y=6-(x-2)^{4}$ at the point on the curve where $x=1$.
- The tangent to the curve $y=\left(\dfrac{x}{2}-1\right)^{6}$, at the point where $x=4$, meets the $y$-axis at $A$. Find the coordinates of $A$.
- Show that the tangent to the curve $y=(x+2 a)^{3}$ at the point where $y=a^{3}$ is $y=3 a^{2} x+4 a^{3} .$
- Find equations of the tangent lines to the curve $y=\dfrac{x+1}{x-1}$ that are parallel to the line $2 y+x=6$.
- The equation of a curve is $y=\dfrac{x^{2}+6}{x-3}$. Find the gradient of tangent to the curve at the point $x=4$. Hence, find the equation of the normal to the curve at $x=4$.
-
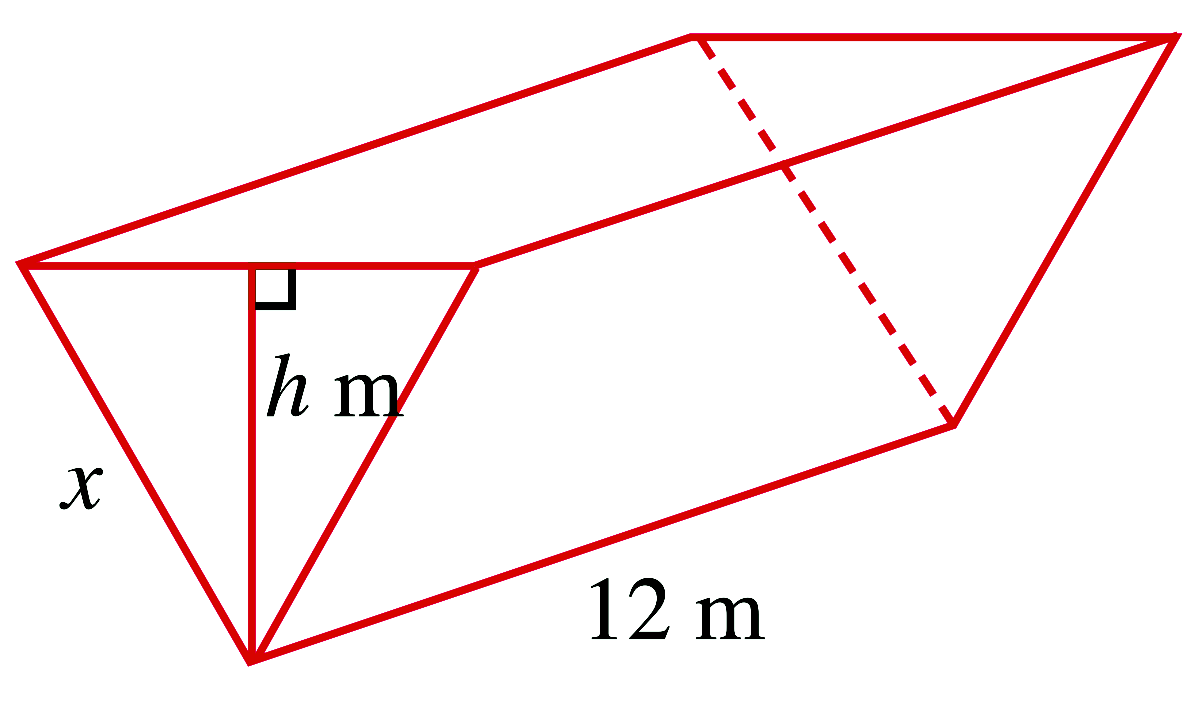
A water trough of length $12 \mathrm{~m}$ has a vertical cross-section in the shape of an
equilateral triangle of sides $x \mathrm{~m}$ and height $h \mathrm{~m}$. Express $V$, the
volume of water that the trough can hold in terms of $h$. When the height of water in the
trough is $1.8 \mathrm{~m}$, its depth is decreasing at a rate of $0.2 \mathrm{~m} / \mathrm{s}$.
Find the rate of change in the volume of water in the trough at this instant.
-
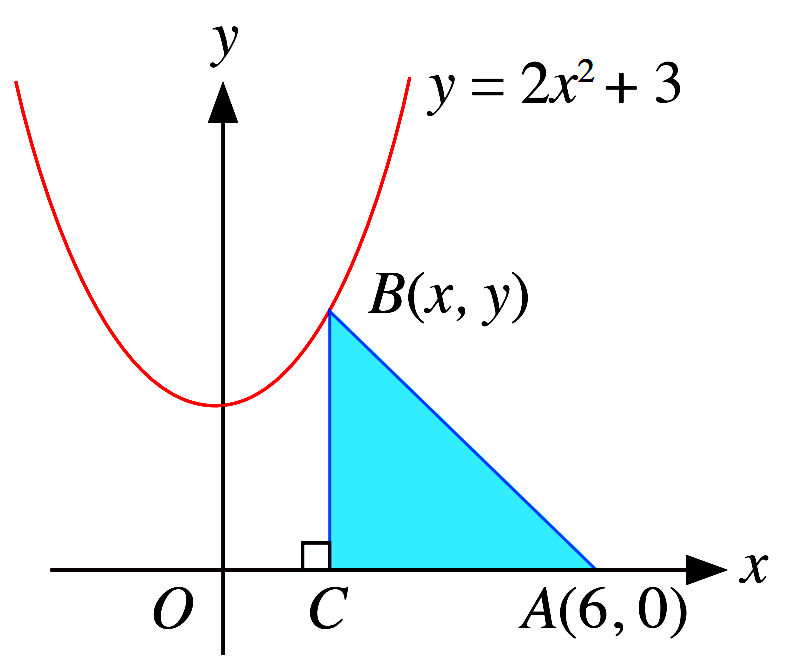
The figure shows part of the curve $y=2 x^{2}+3$. The point $B(x, y)$ is a variable point
that moves along the curve for $0 < x <6$. $C$ is a point on the $x$-axis such that $B C$ is
parallel to the $y$-axis and $A(6,0)$ lies on the $x$-axis. Express the area of the triangle
$A B C, S \mathrm{~cm}^{2}$, in terms of $x$, and find an expression for
$\dfrac{dS}{dx} .$ Given that when $x=2$, $S$ is
increasing at the rate of $0.8 \mathrm{~unit}^{2} / \mathrm{s}$, find the corresponding
rate of change of $x$ at this instant.
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!

