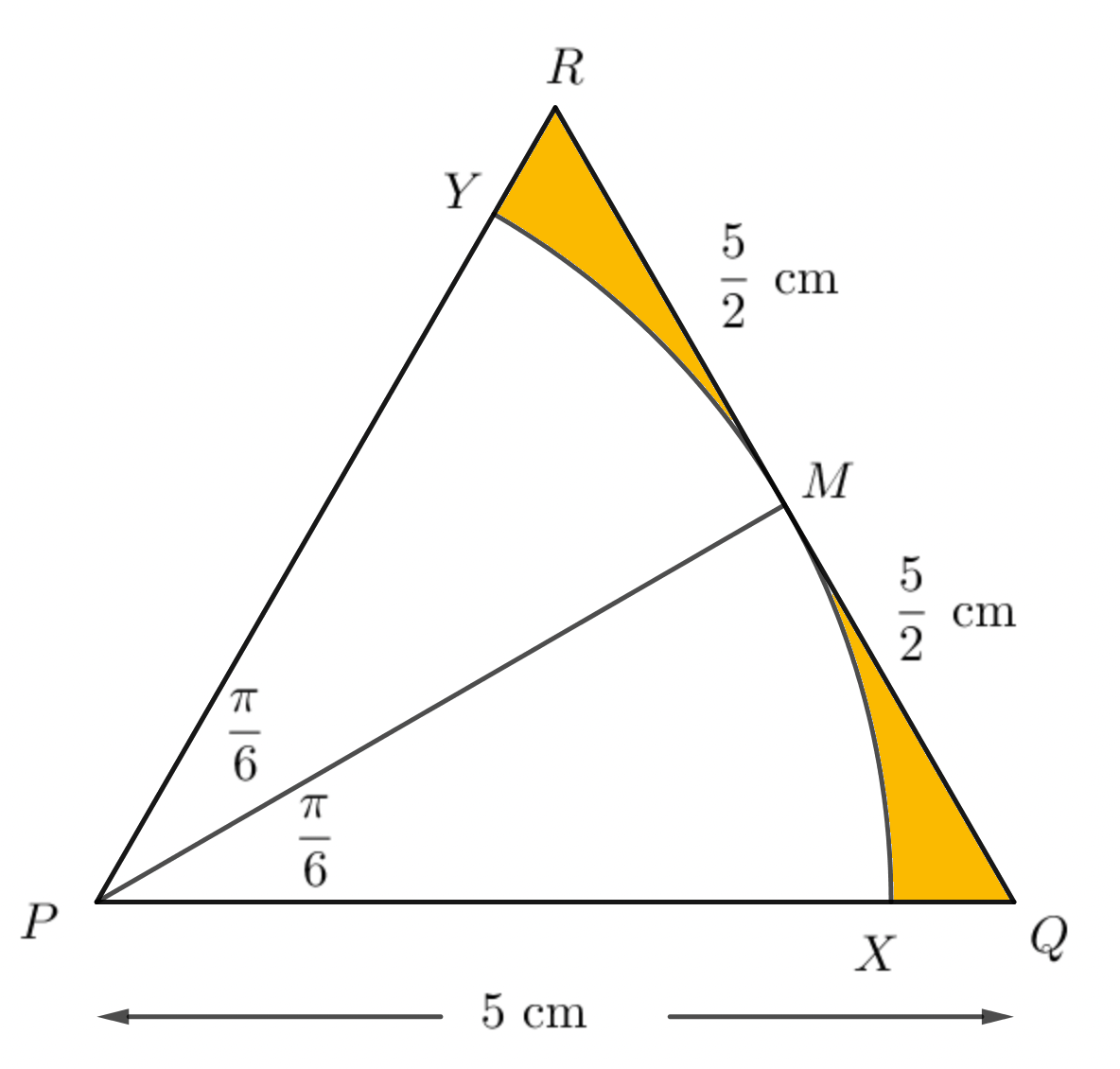
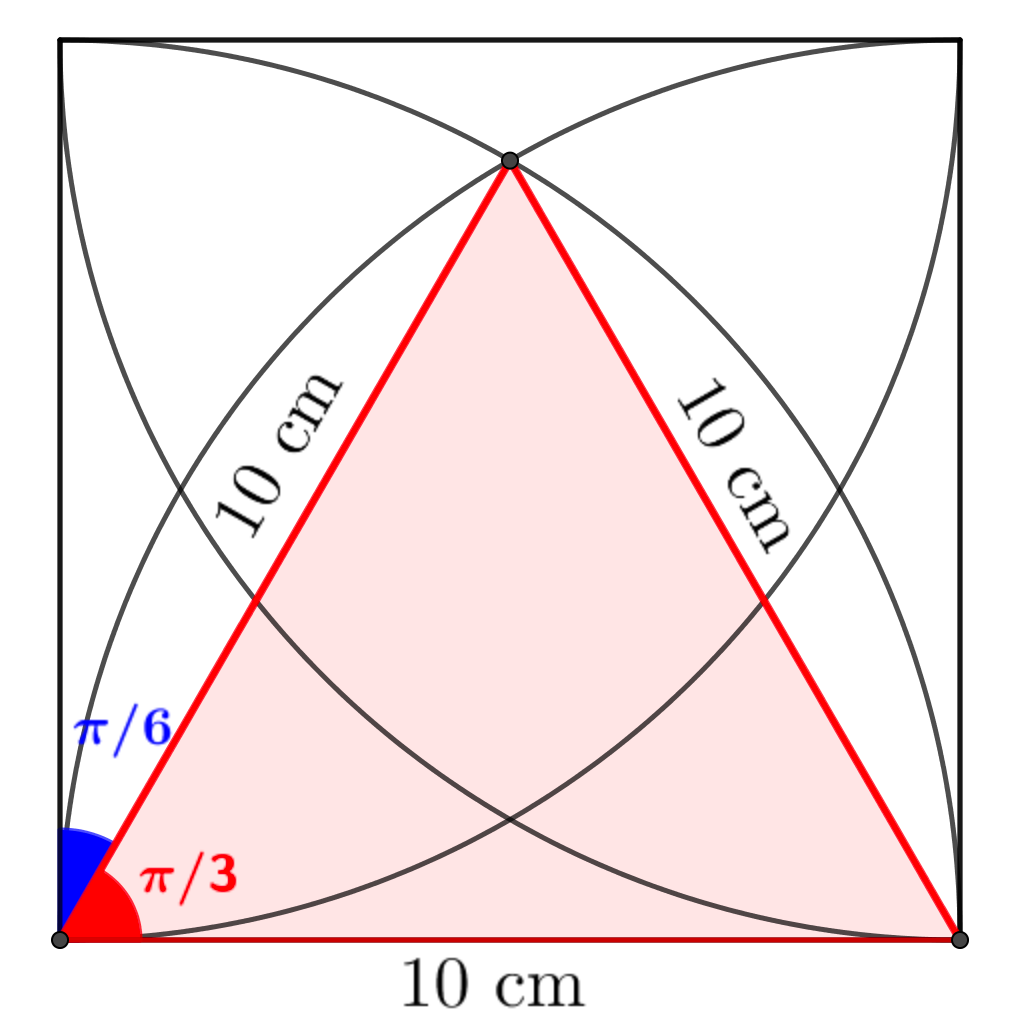
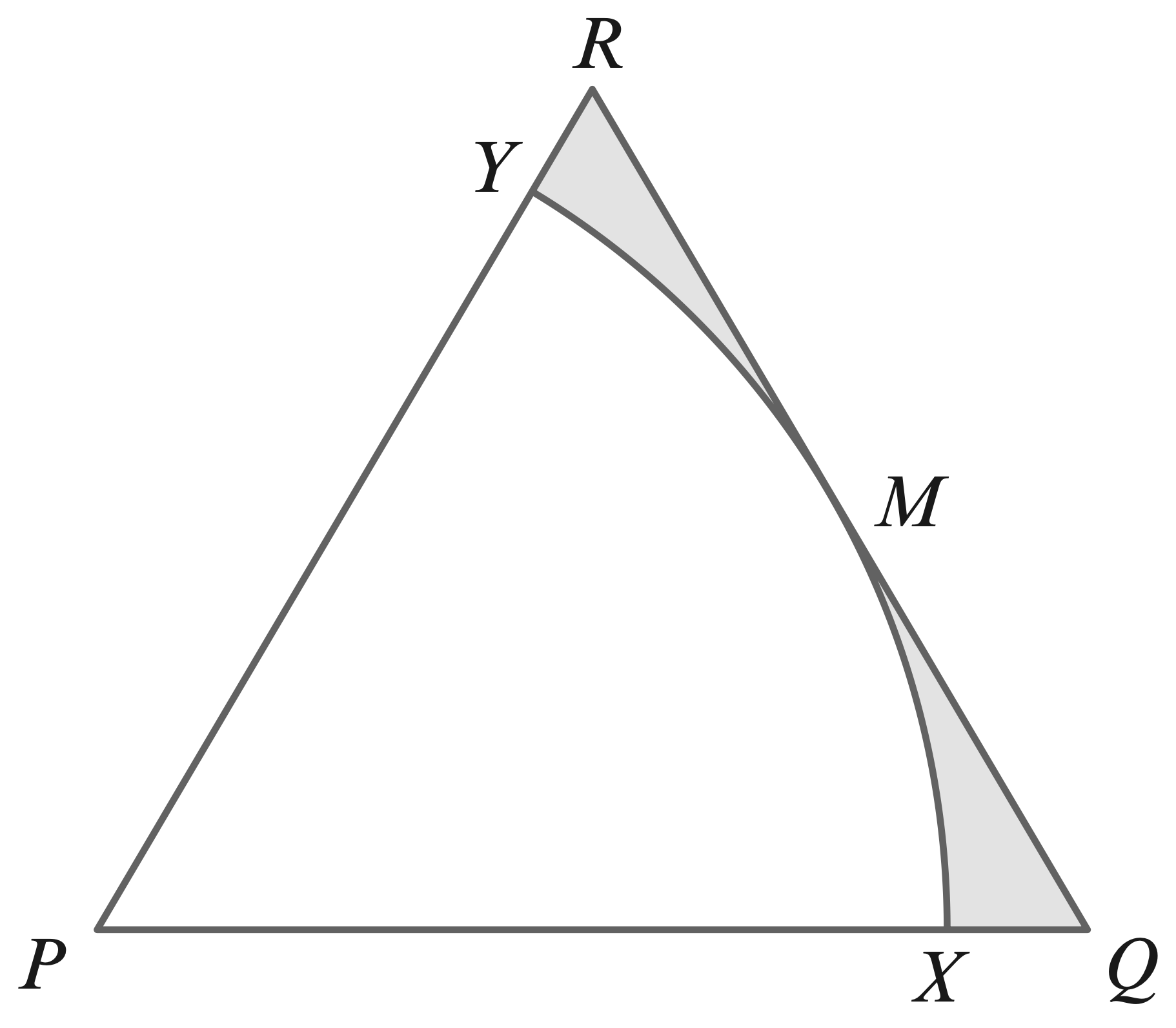
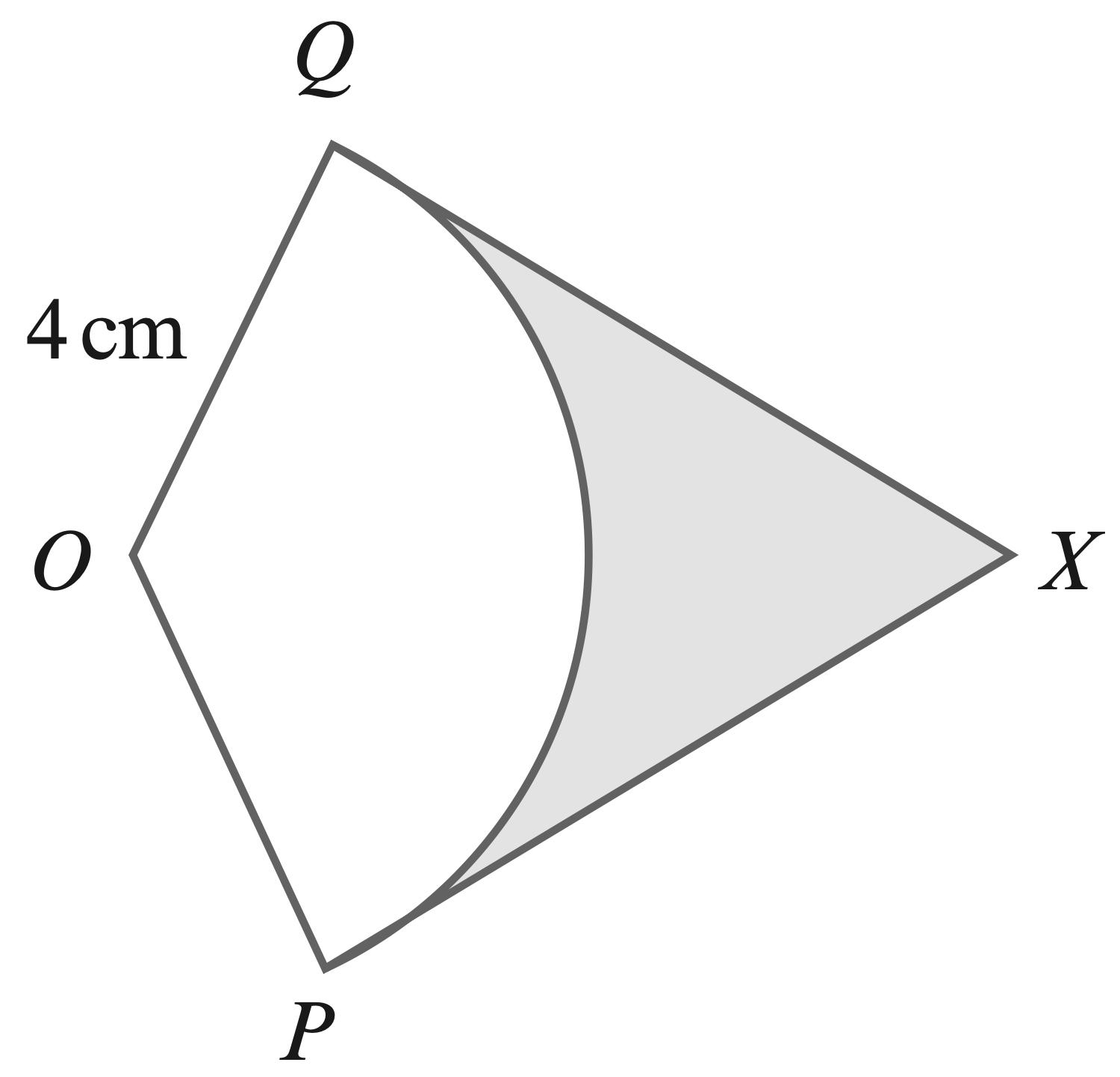
- The diagram shows ane quilateral triangle, $PQR$, with side length $5$ cm.
$M$ is the midpoint of the line $QR$. An arc of a circle, centre $P$, touches $QR$
at $M$ and meets $PQ$ at $X$ and $PR$ at $Y$.
Find in terms of $\pi$ and $\sqrt{3}:$
(a) the total perimeter of the shaded region.
(b) the total area of the shaded region.
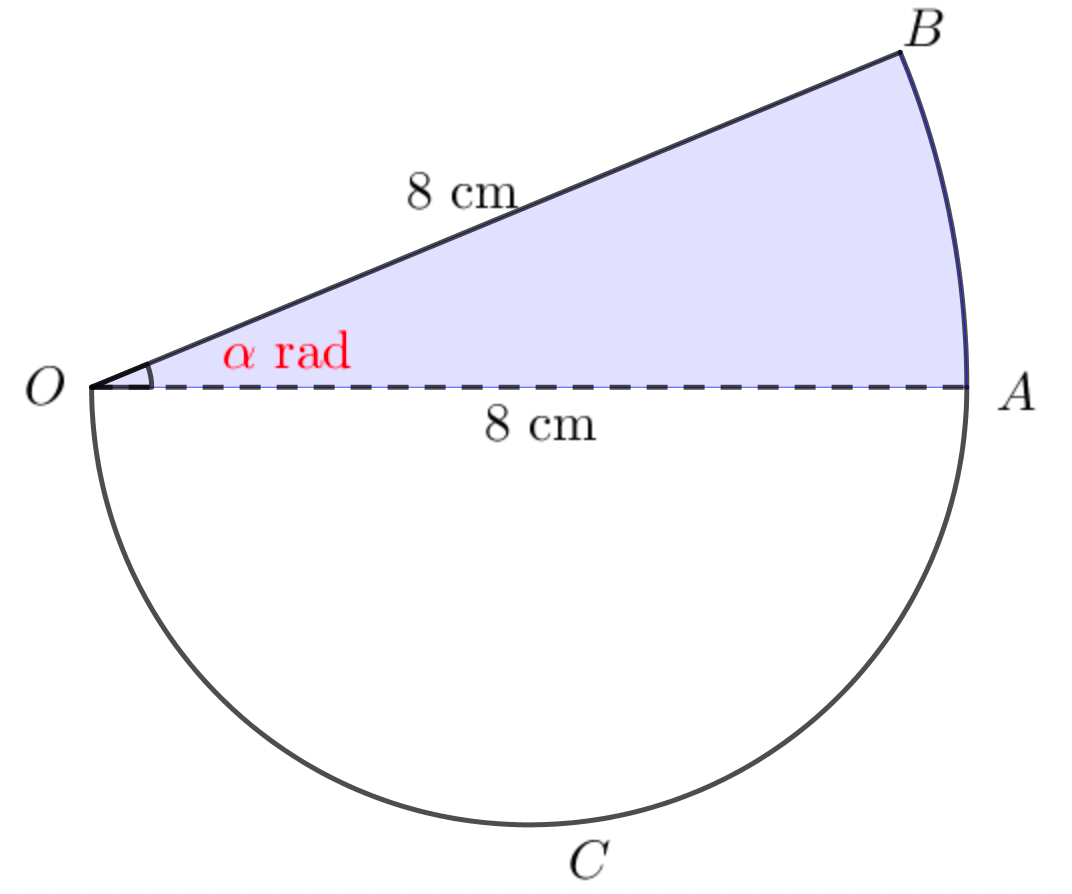
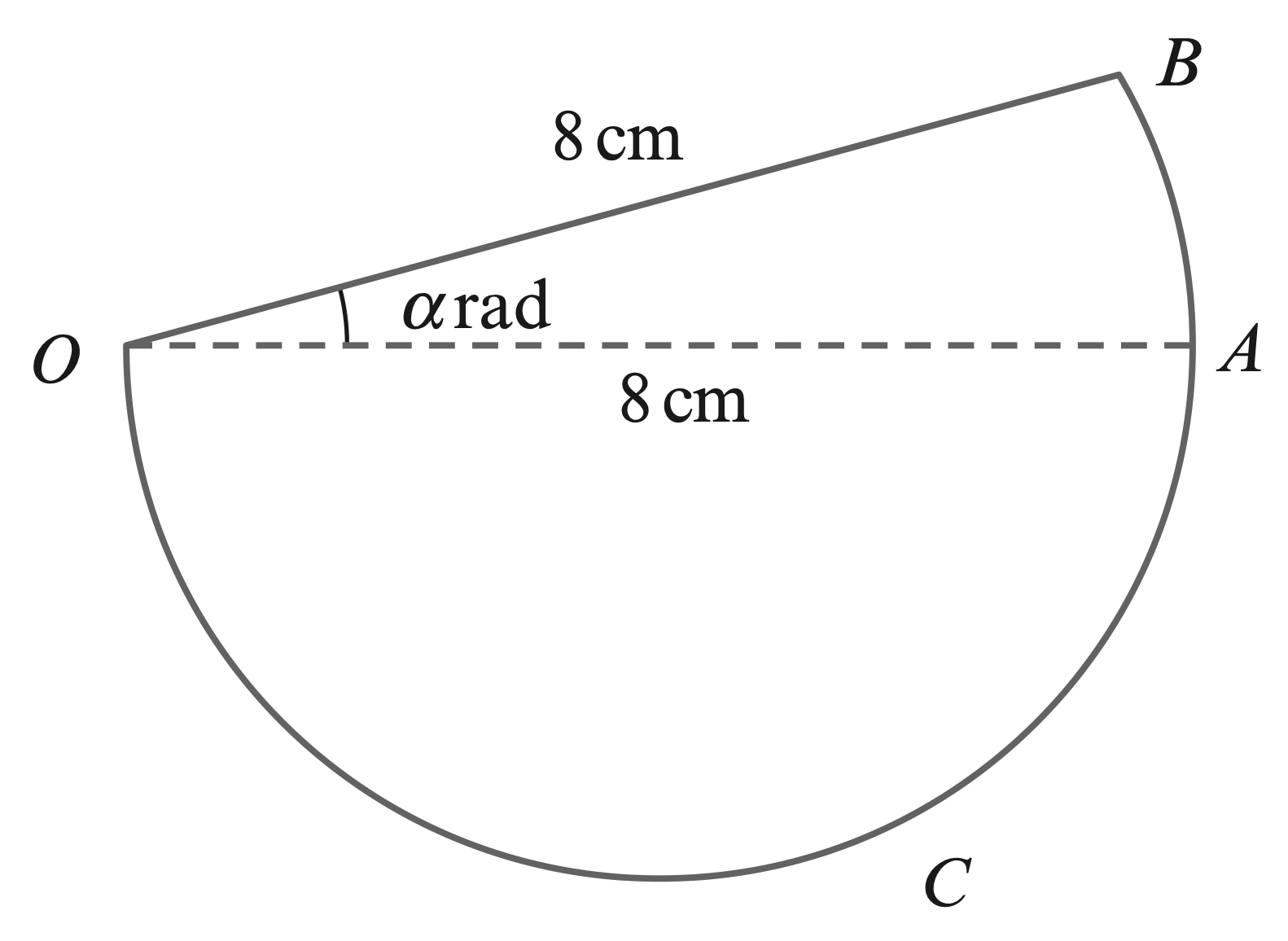
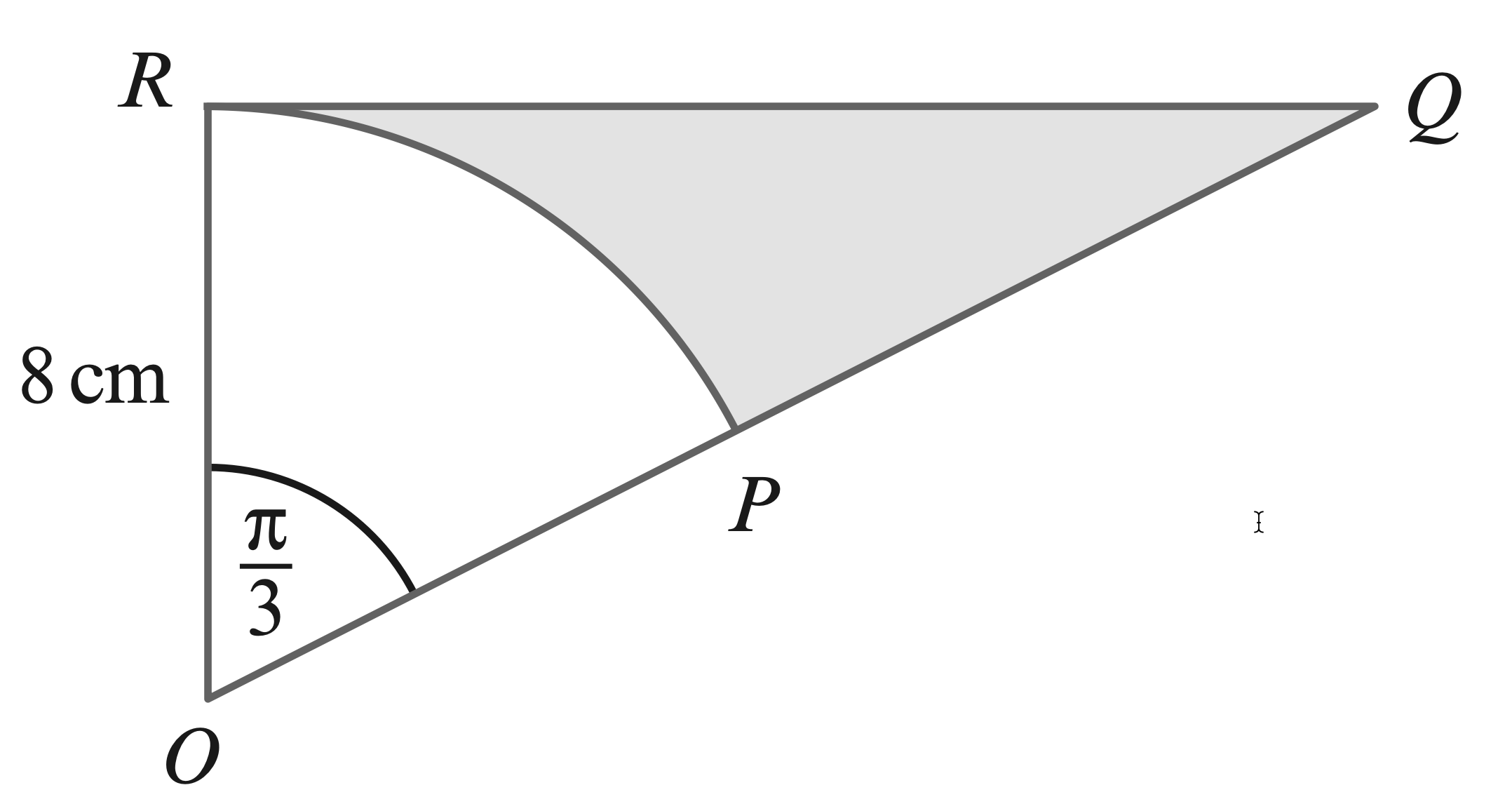
- In the diagram, $OAB$ is a sector of a circle with centre $O$ and radius $8$ cm.
Angle $BOA$ is $\alpha$ radians. $OAC$ is a semicircle with diameter $OA$.
The area of the semicircle $OAC$ is twice the area of the sector $OAB$.
(a) Find $\alpha$ in terms of $\pi$.
(b) Find the perimeter of the complete figure in terms of $\pi$.
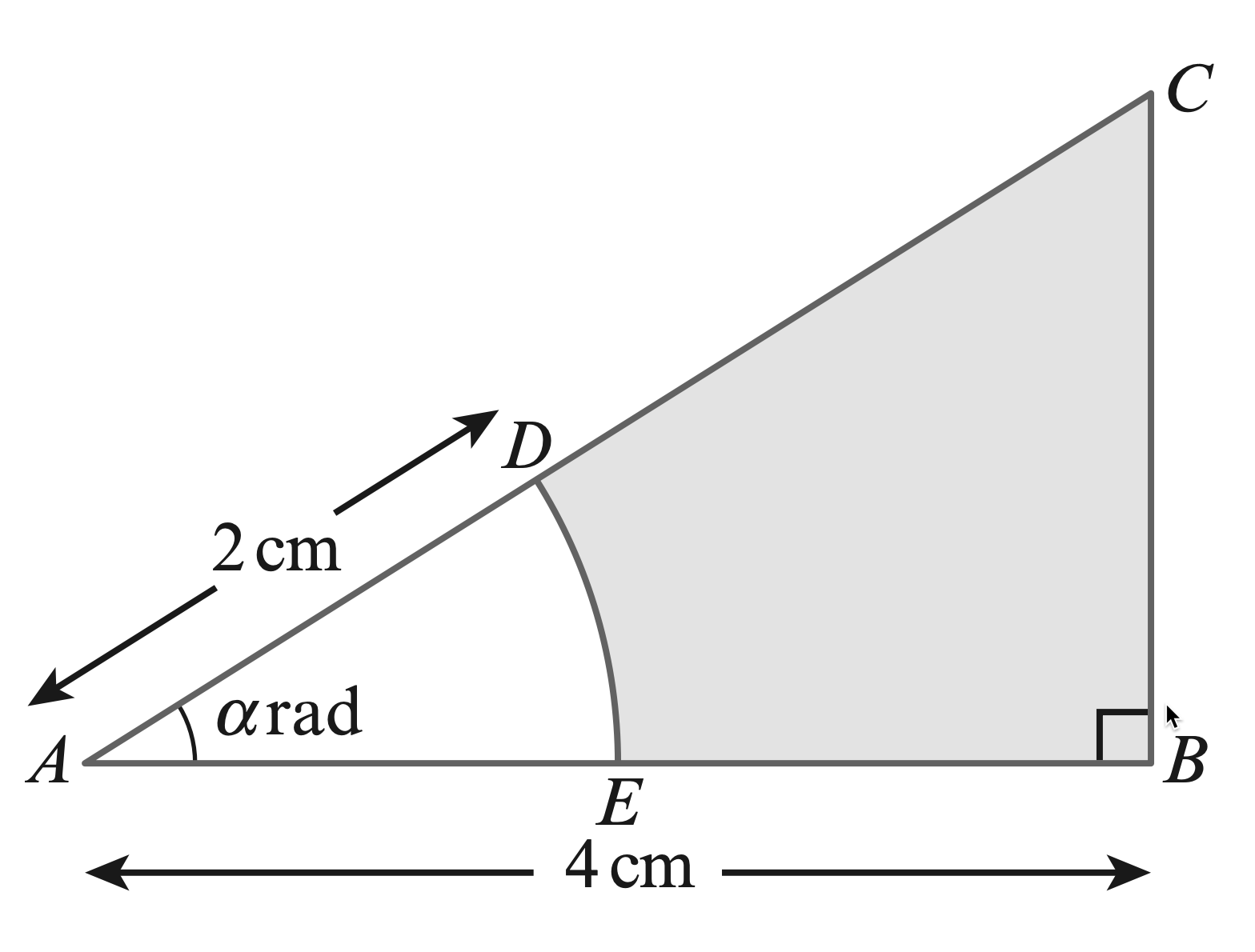
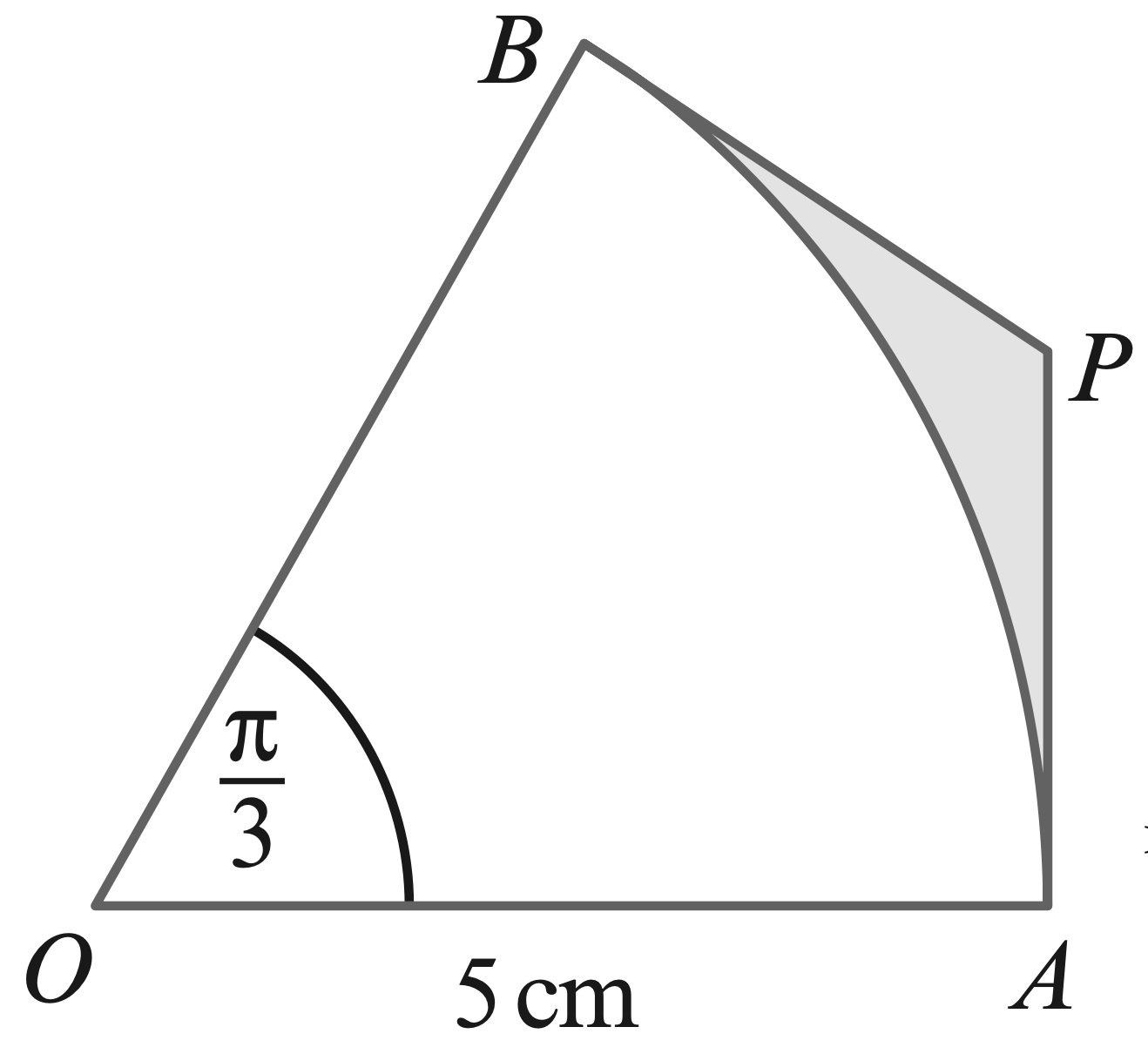
- The diagram shows triangle $ABC$ in which $AB$ is perpendicular to $BC$.
The length of $AB$ is $4$ cm and angle $CAB$ is $\alpha$ radians. The arc
$DE$ with centre $A$ and radius $2$ cm meets $AC$ at $D$ and $AB$ at $E$ .
Find, in terms of $\alpha$,
(a) the area of the shaded region,
(b) the perimeter of the shaded region.
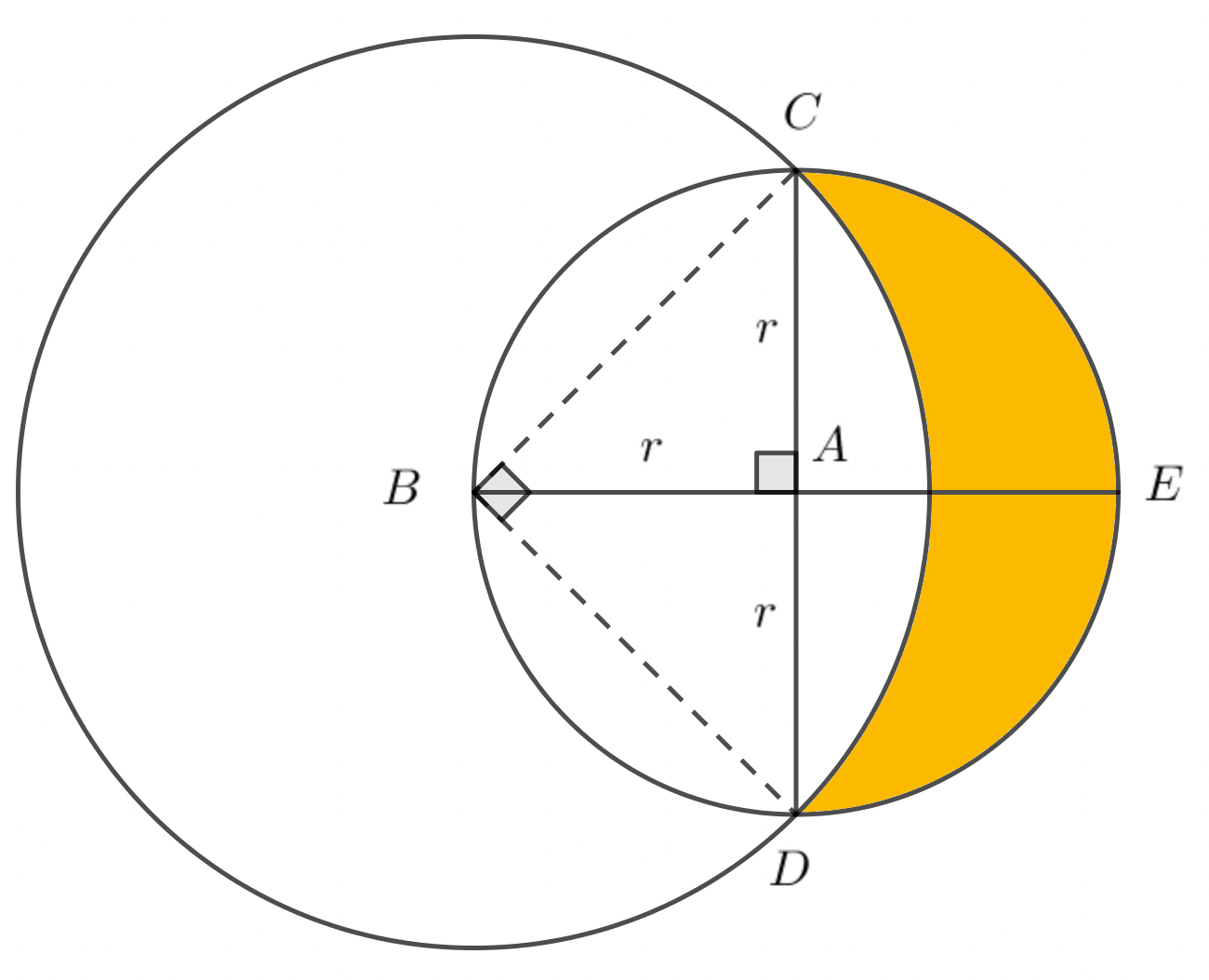
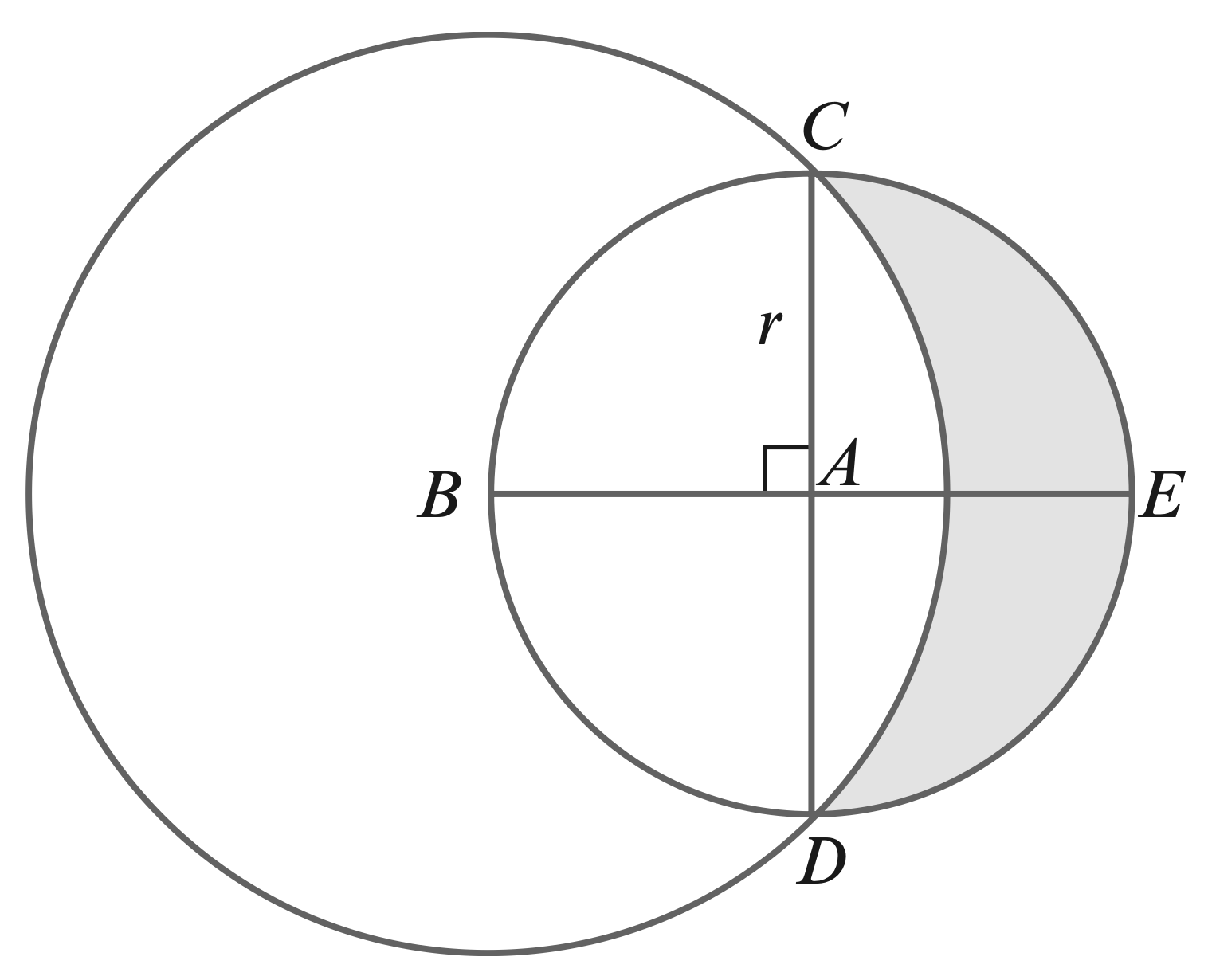
- The diagram shows a circle with centre $A$ and radius $r$.
Diameters $CAD$ and $BAE$ are perpendicular to each other.
A larger circle has centre $B$ and passes through $C$ and $D$.
(a) Show that the radius of the larger circle is $r\sqrt{2} $.
(b) Find the area of the shaded region in terms of $r$.
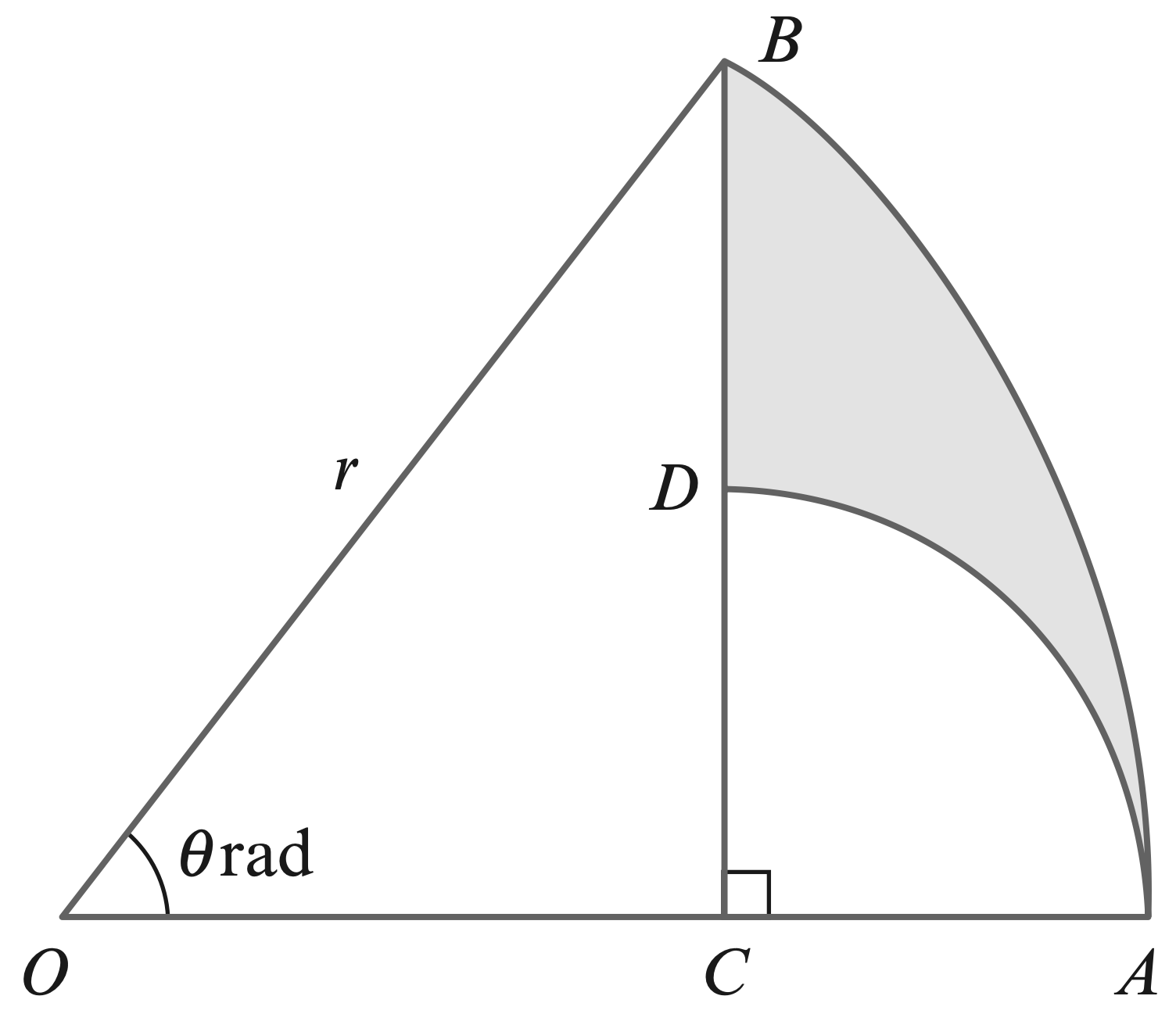
- The diagram shows a sector $OAB$ of a circle with centre $O$ and radius $r$.
Angle AOB is $\theta$ radians. The point $C$ on $OA$ is such that $BC$ is
perpendicular to $OA$. The point $D$ is on $BC$ and the circular arc $AD$ has
centre $C$.
(a) Find $AC$ in terms of $r$ and $\theta$.
(b) Find the perimeter of the shaded region $ABD$ when $\theta= \dfrac{1}{3}\pi$
and $r = 4$, giving your answer as an exact value.
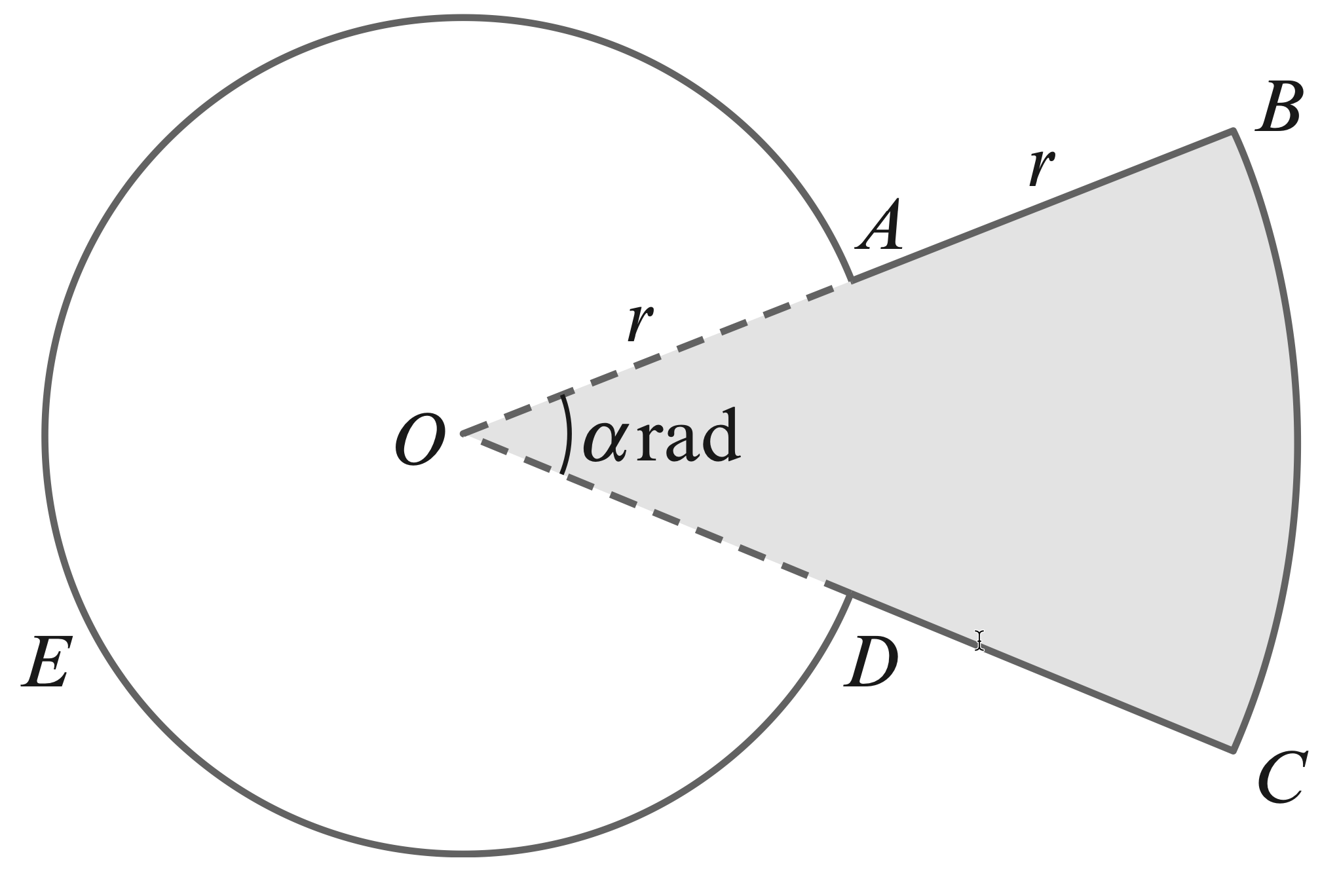
- The diagram shows a sector, $P O Q$, of a circle, centre $O$, with radius
$4 \mathrm{~cm}$. The length of arc $P Q$ is $7 \mathrm{~cm}$.
The lines $P X$ and $Q X$ are tangents to the circle at $P$ and $Q$, respectively.
(a) Find angle $P O Q$, in radians.
(b) Find the length of $P X$.
(c) Find the area of the shaded region.
- The diagram shows a sector, $P O R$, of a circle, centre $O$, with radius
$8 \mathrm{~cm}$ and sector angle $\dfrac{\pi}{3}$ radians.
The lines $O R$ and $Q R$ are perpendicular and $O P Q$ is a straight line.
Find the exact area of the shaded region.
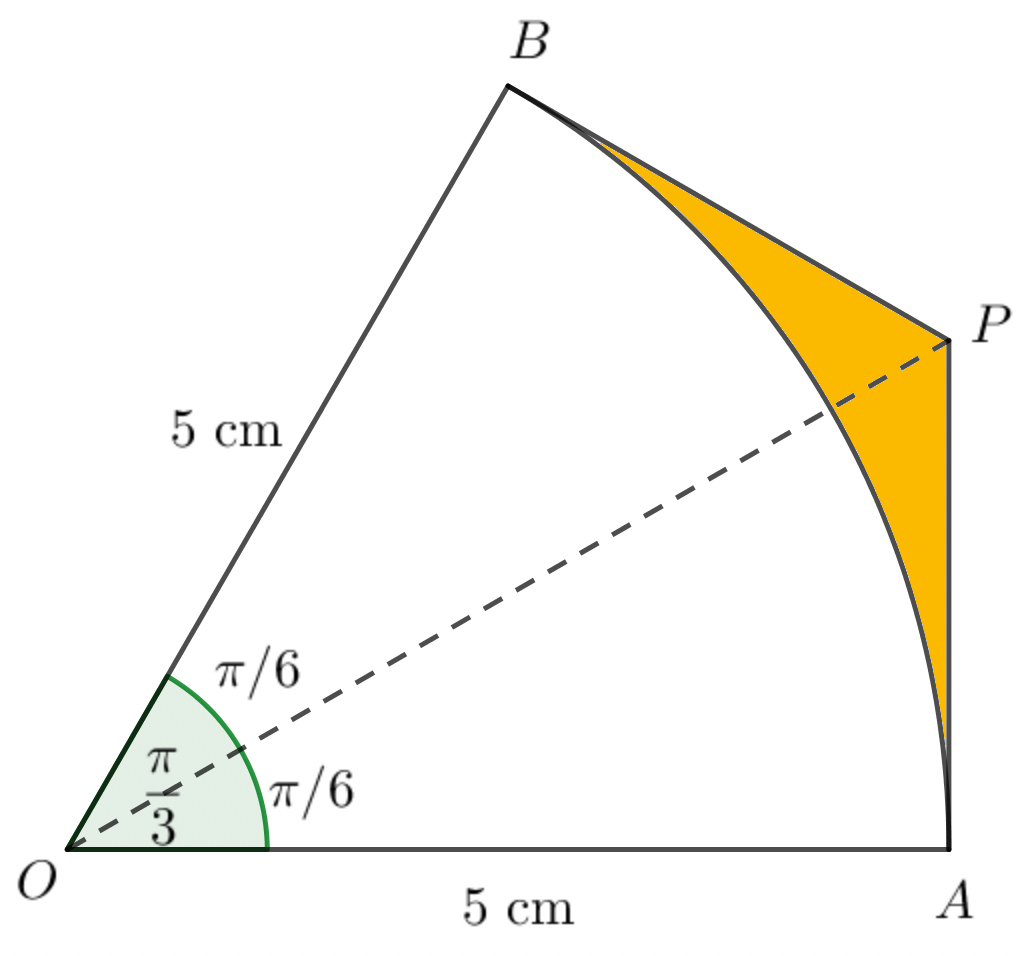
- The diagram shows a sector, $A O B$, of a circle, centre $O$, with radius
$5 \mathrm{~cm}$ and sector angle $\dfrac{\pi}{3}$ radians.
The lines $A P$ and $B P$ are tangents to the circle at $A$ and $B$, respectively.
(a) Find the exact length of $A P$.
(b) Find the exact area of the shaded region.
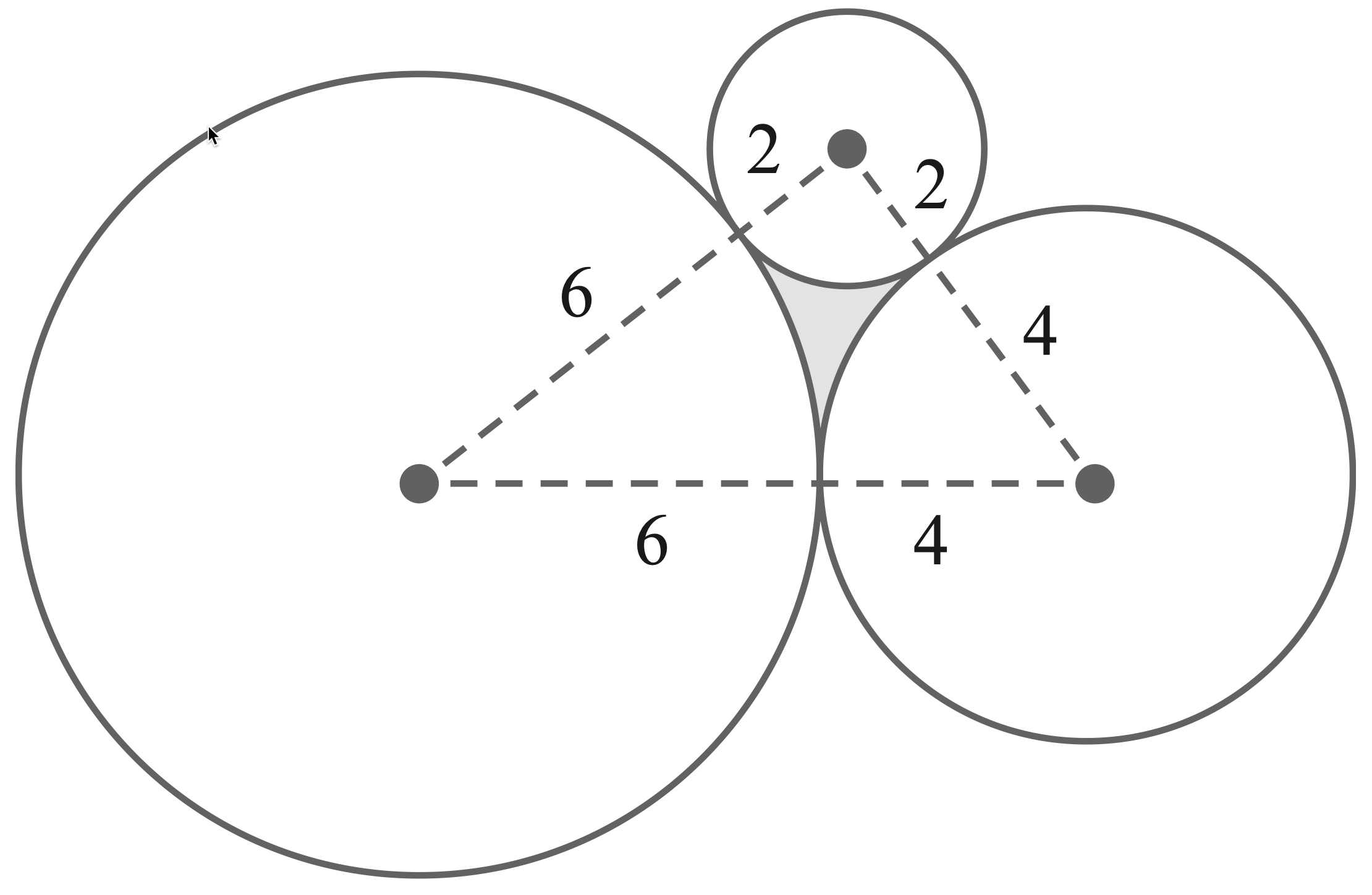
- The diagram shows three touching circles with radii $6 \mathrm{~cm}, 4 \mathrm{~cm}$ and $2 \mathrm{~cm}$.
Find the area of the shaded region.
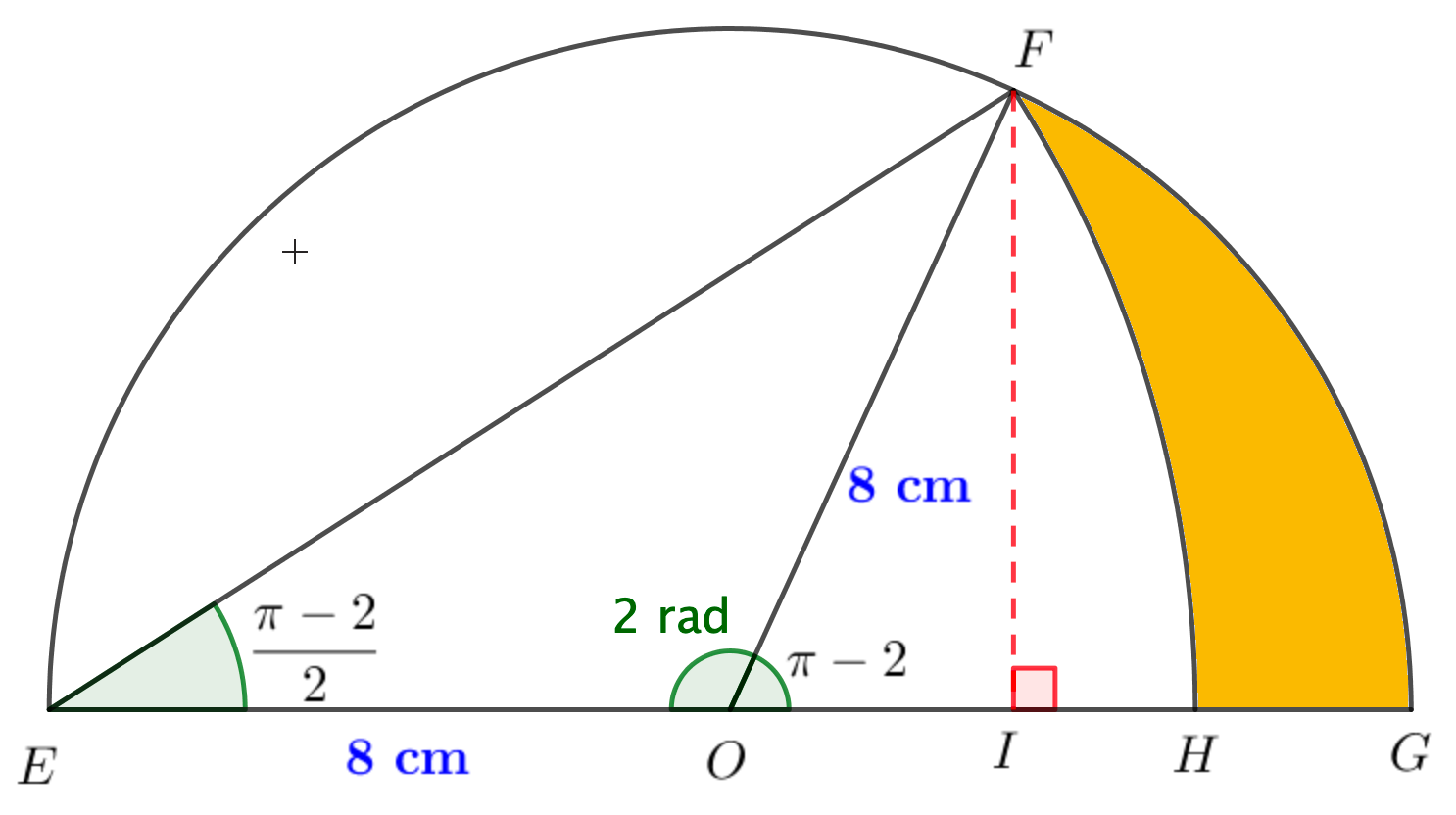
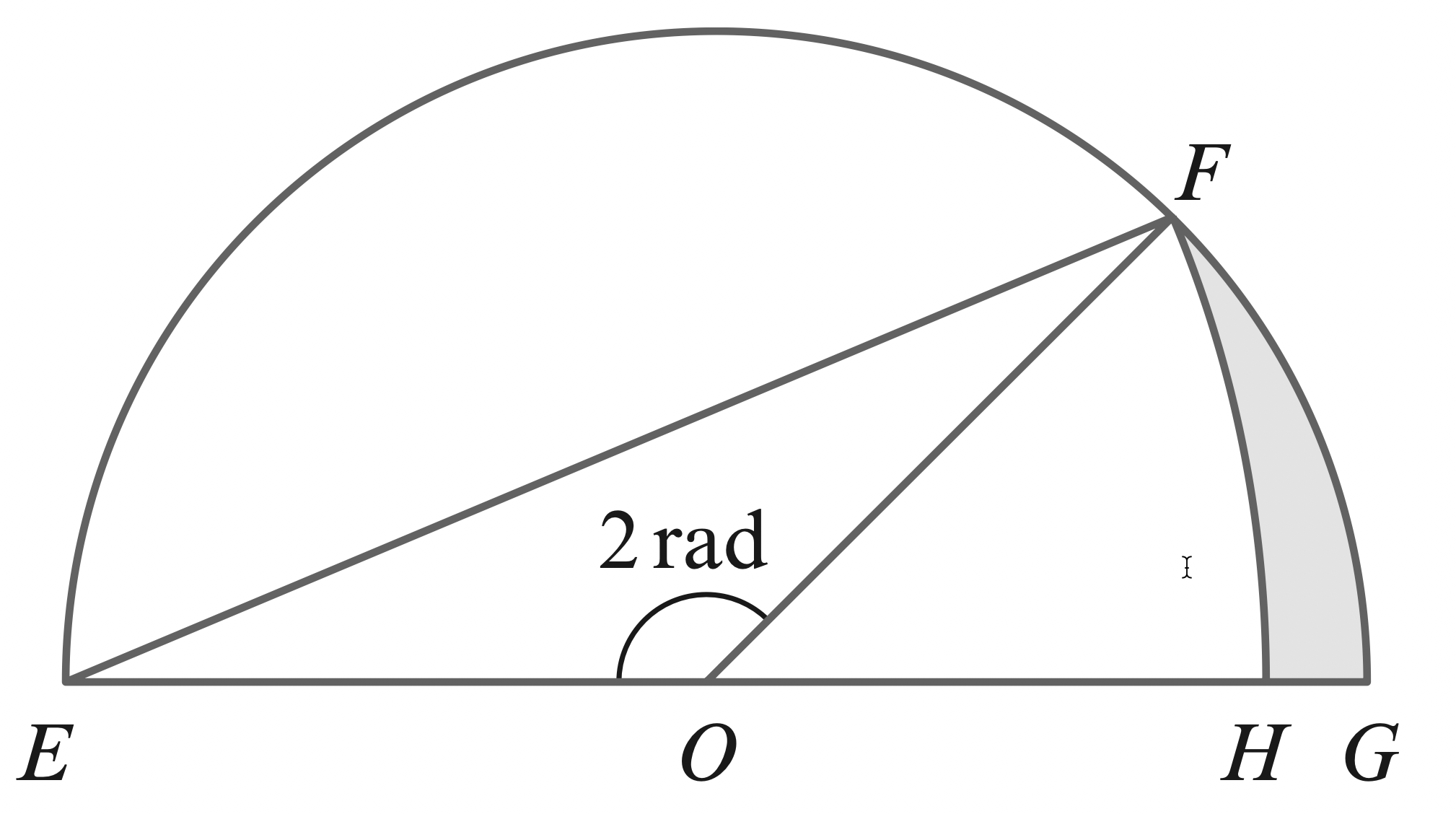
- The diagram shows a semicircle, centre $O$, with radius $8 \mathrm{~cm} .$
$F H$ is the arc of a circle, centre $E$. Find the area of:
(a) triangle $E O F$
(b) sector $F O G$
(c) sector $F E H$
(d) the shaded region.
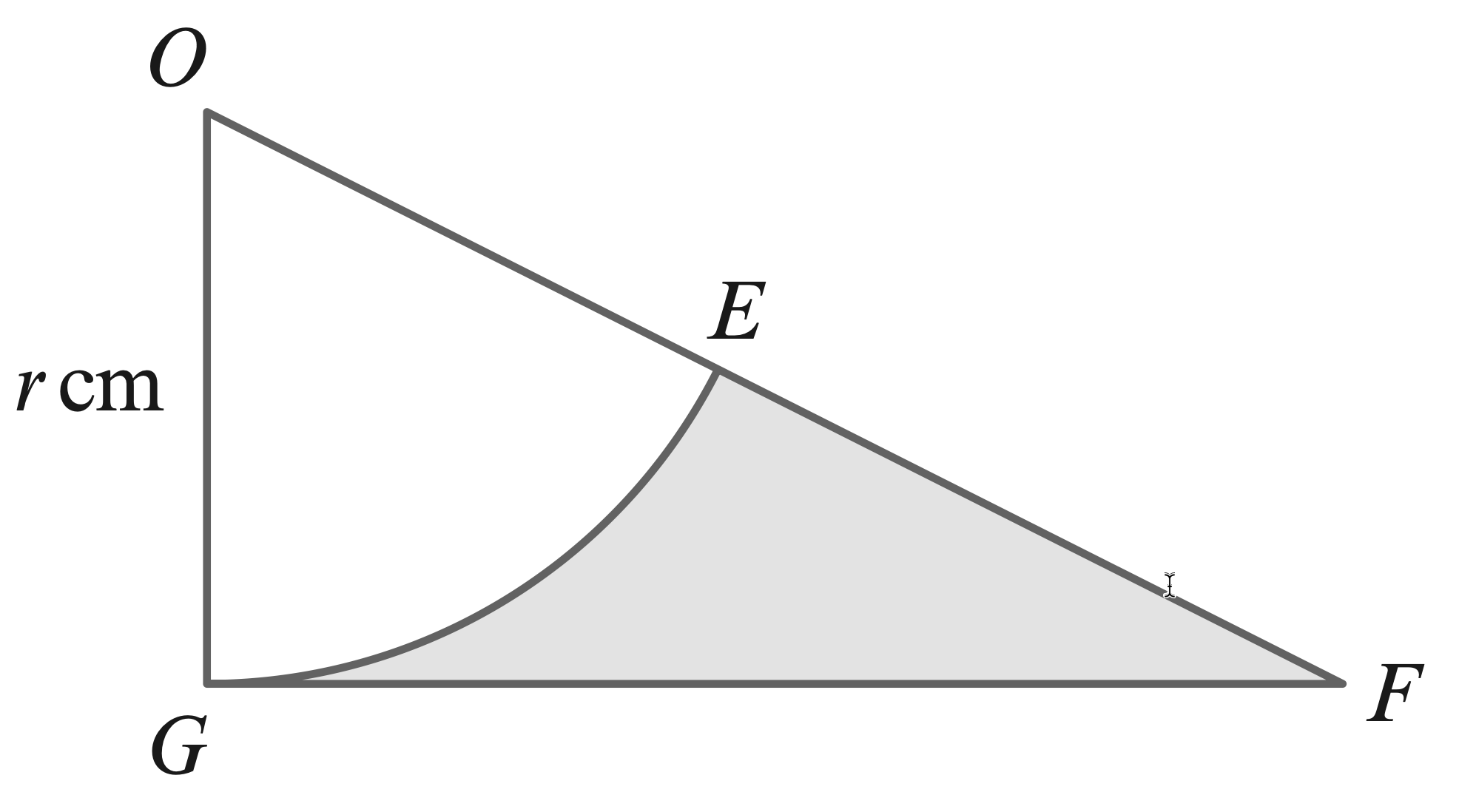
- The diagram shows a sector, $E O G$, of a circle, centre $O$, with radius $r \mathrm{~cm} .$
The line $G F$ is a tangent to the circle at $G$, and $E$ is the midpoint of $O F$.
(a) The perimeter of the shaded region is $P \mathrm{~cm}$. Show that $P=\dfrac{r}{3}(3+3 \sqrt{3}+\pi)$.
(b) The area of the shaded region is $A \mathrm{~cm}^{2}$. Show that $A=\dfrac{r^{2}}{6}(3 \sqrt{3}-\pi)$.
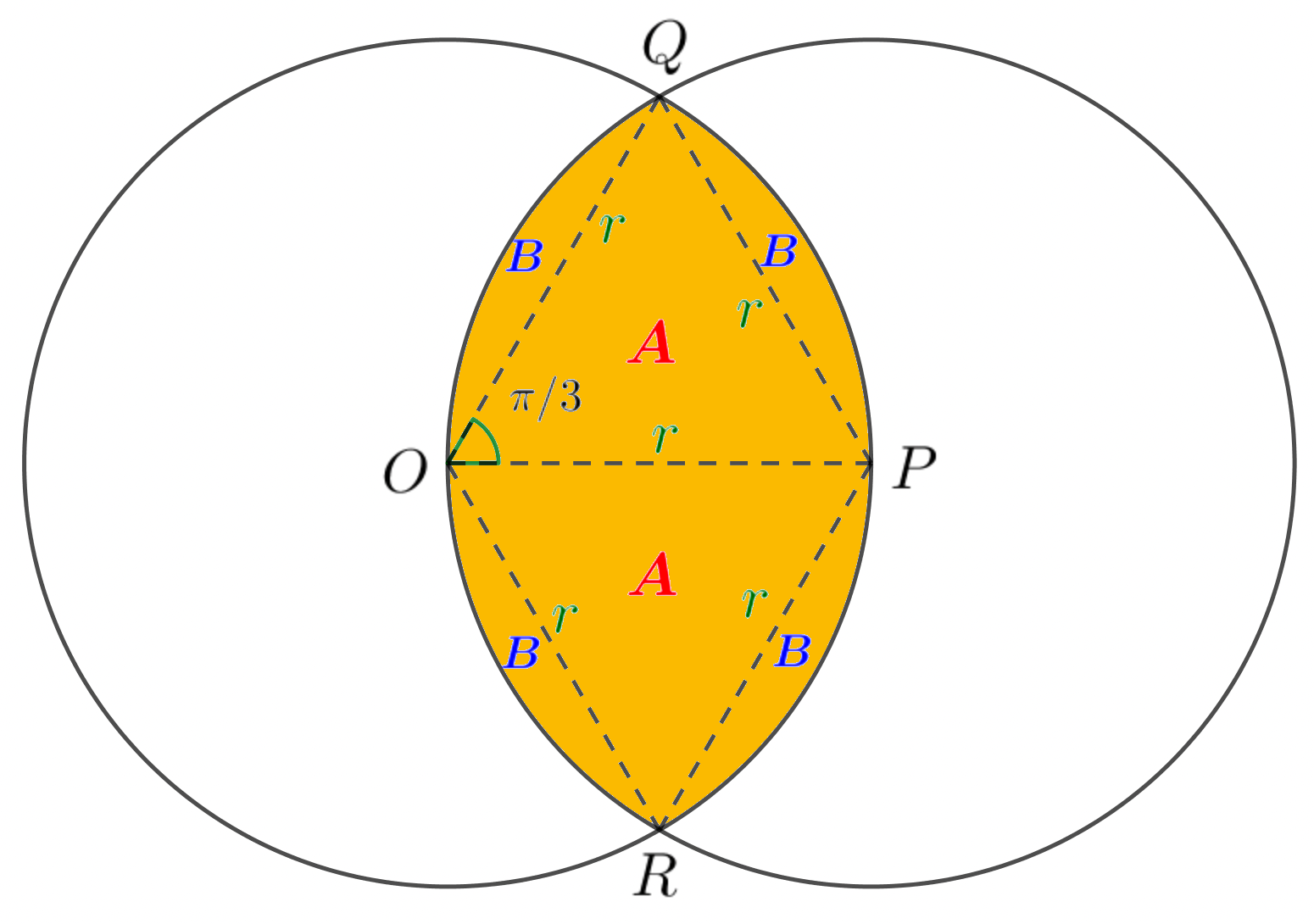
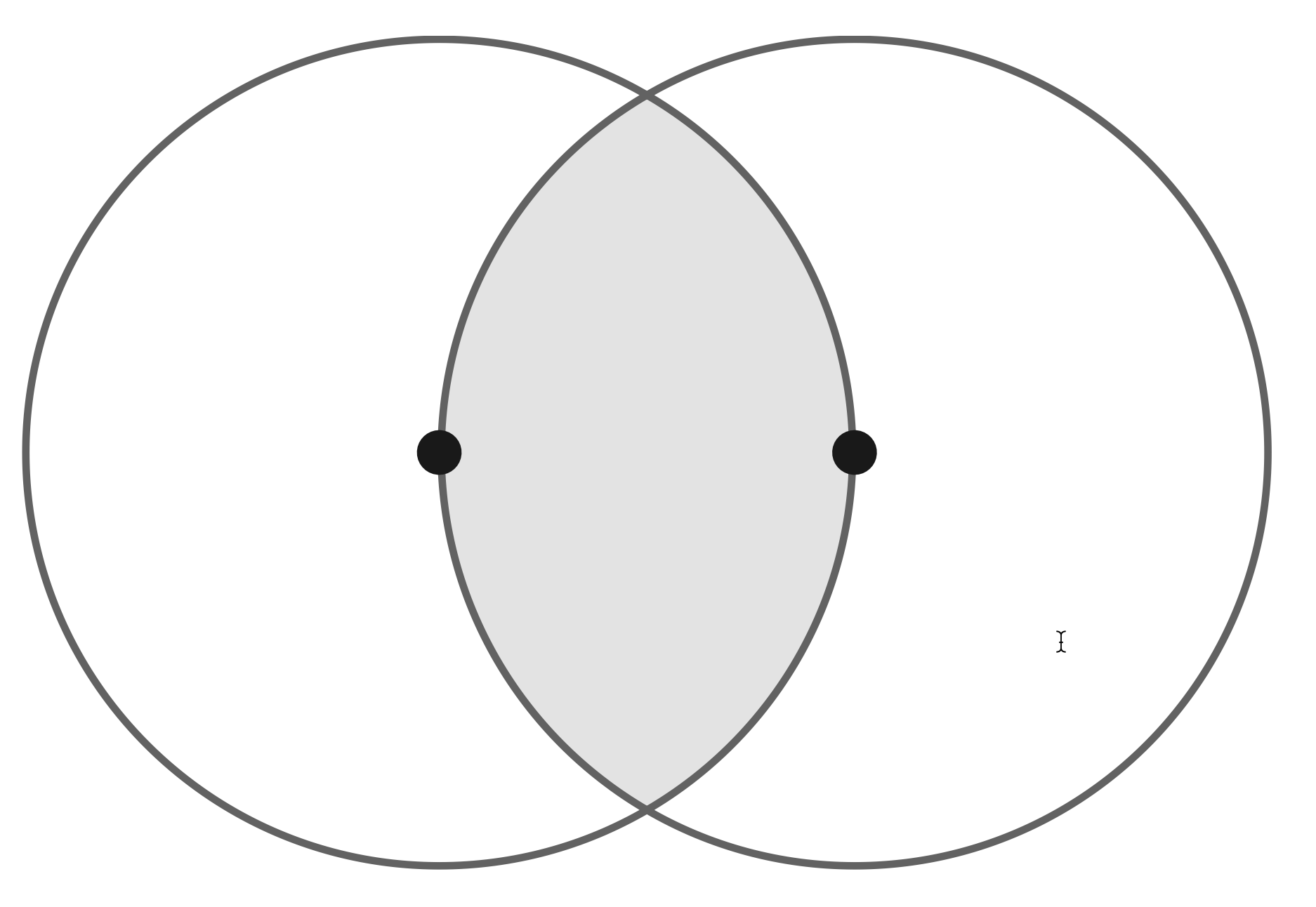
- The diagram shows two circles with radius $r \mathrm{~cm}$.
The centre of each circle lies on the circumference of the other circle.
Find, in terms of $r$, the exact area of the shaded region.
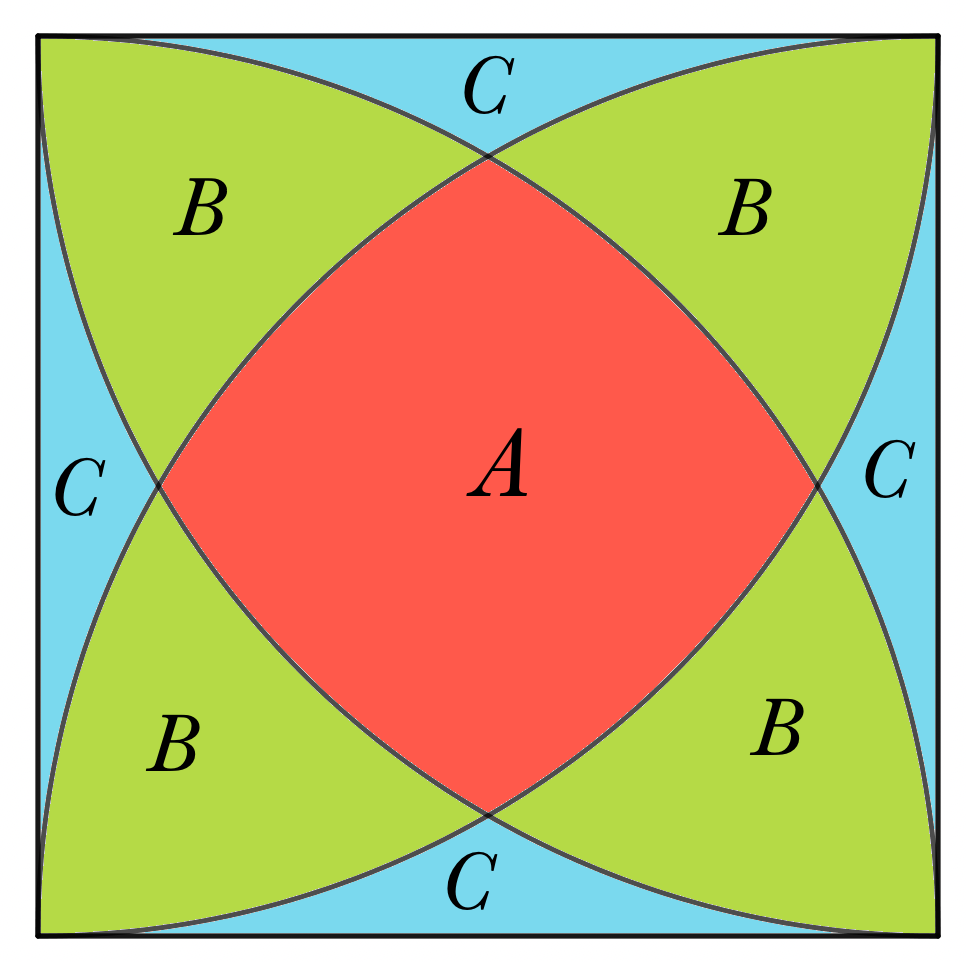
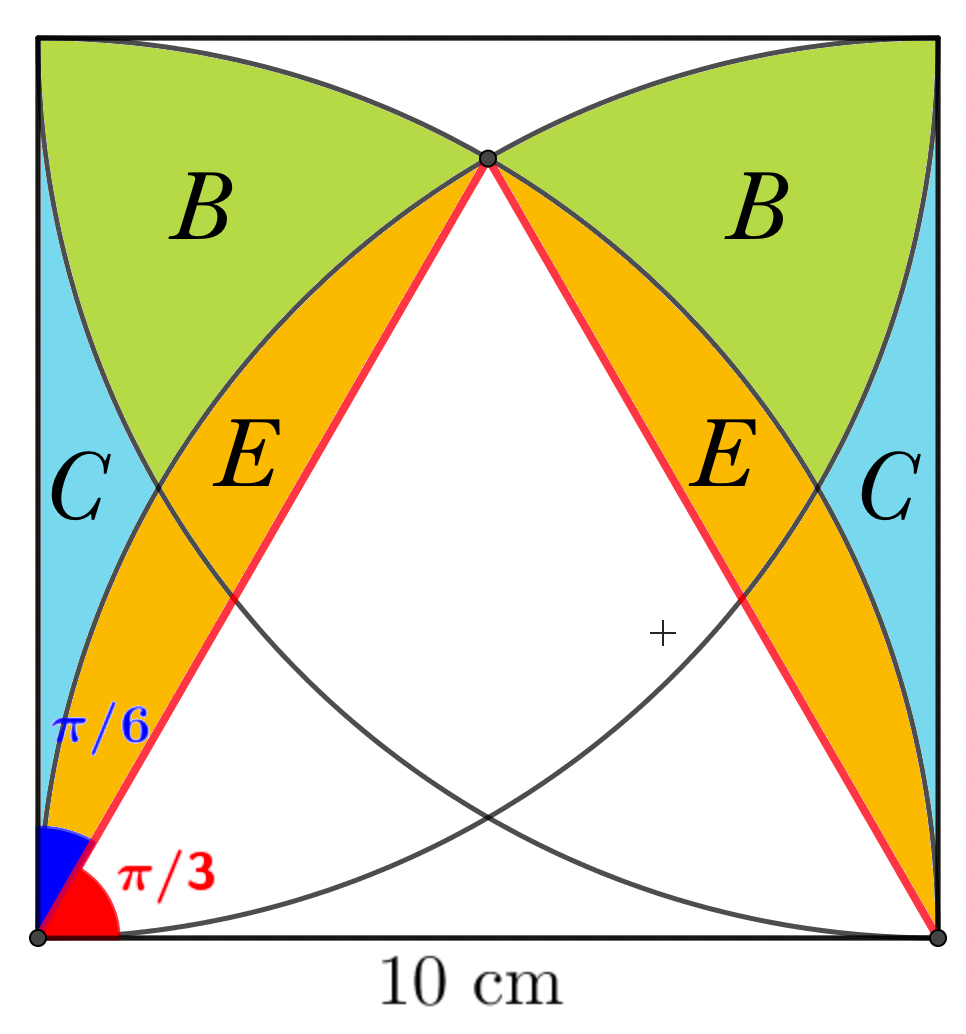
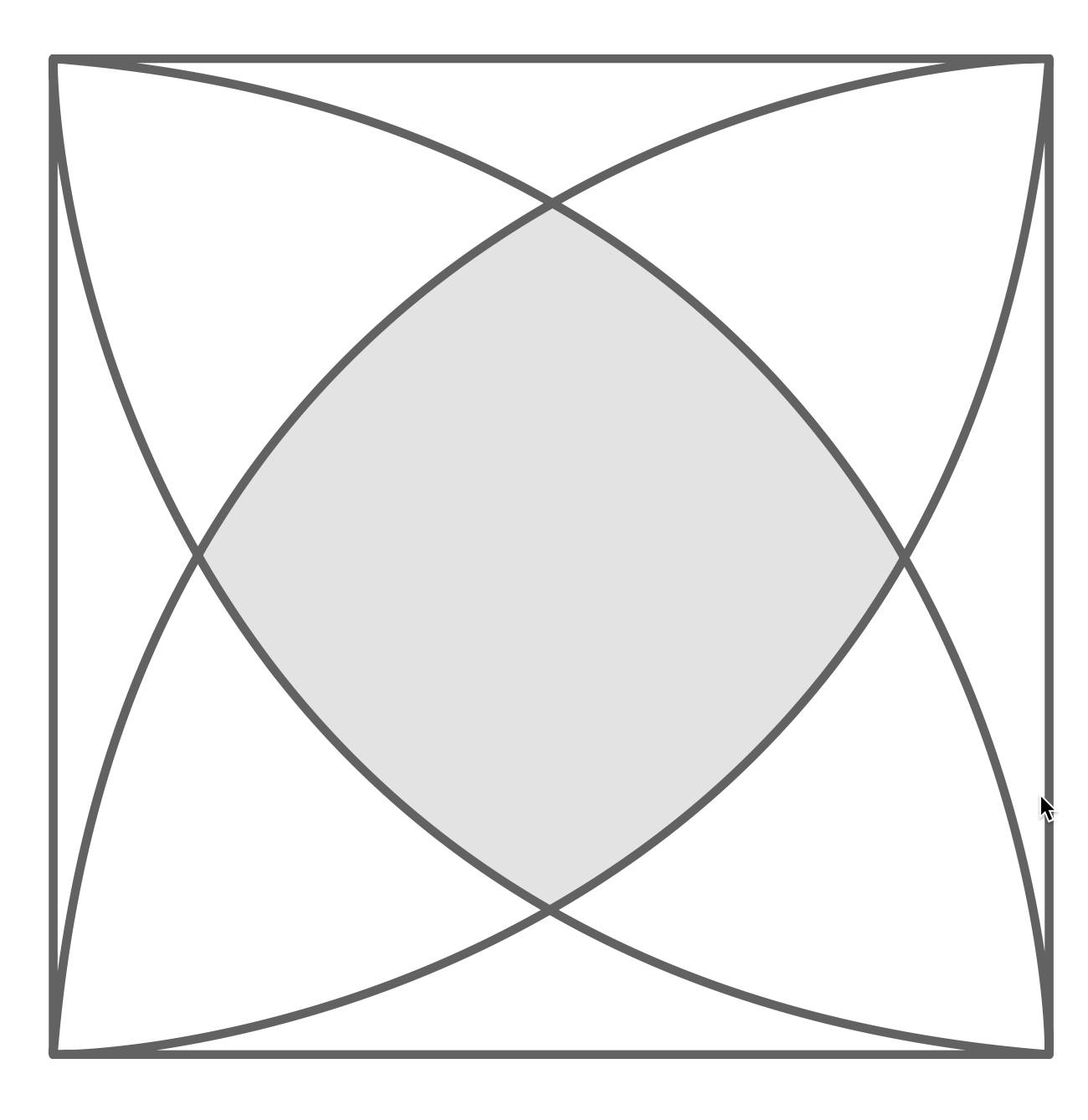
- The diagram shows a square of side length $10$ cm.
A quarter circle, of radius $10$ cm, is drawn from each vertex of the square.
Find the exact area of the shaded region.
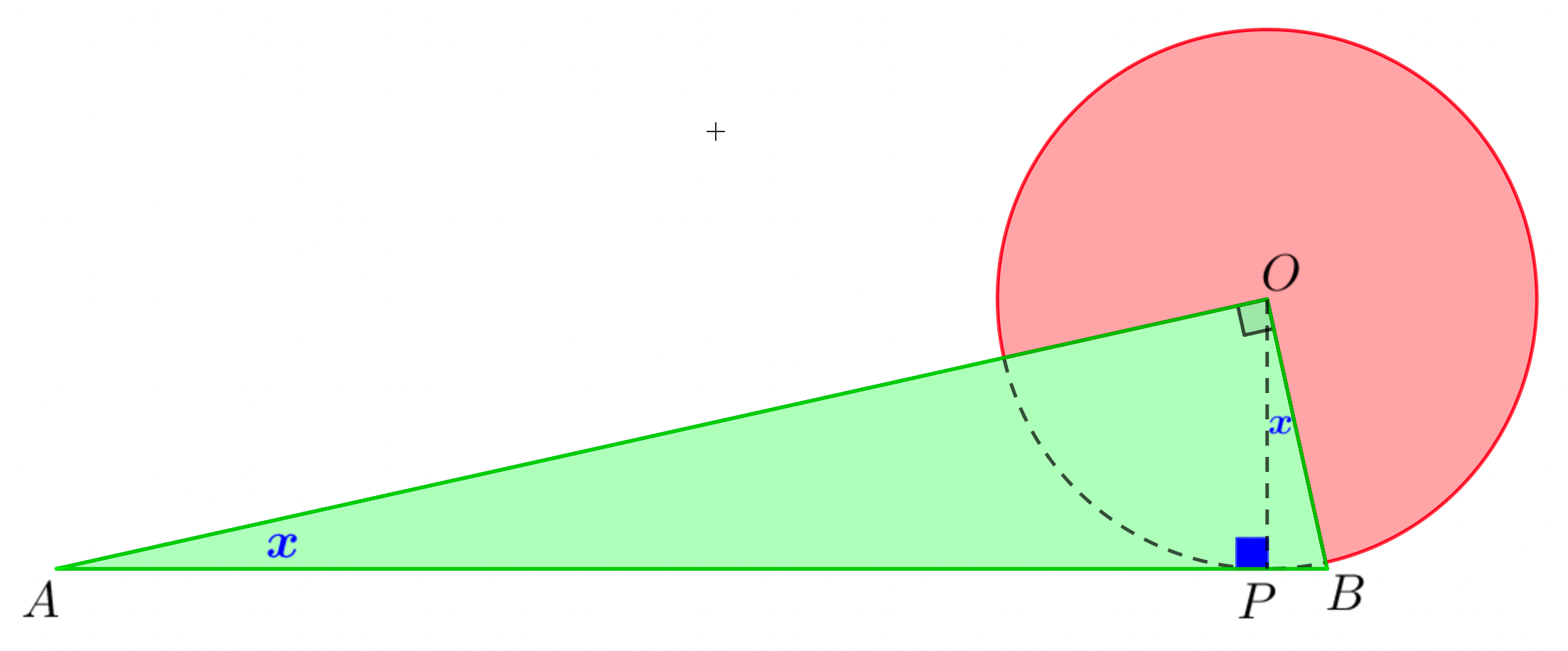
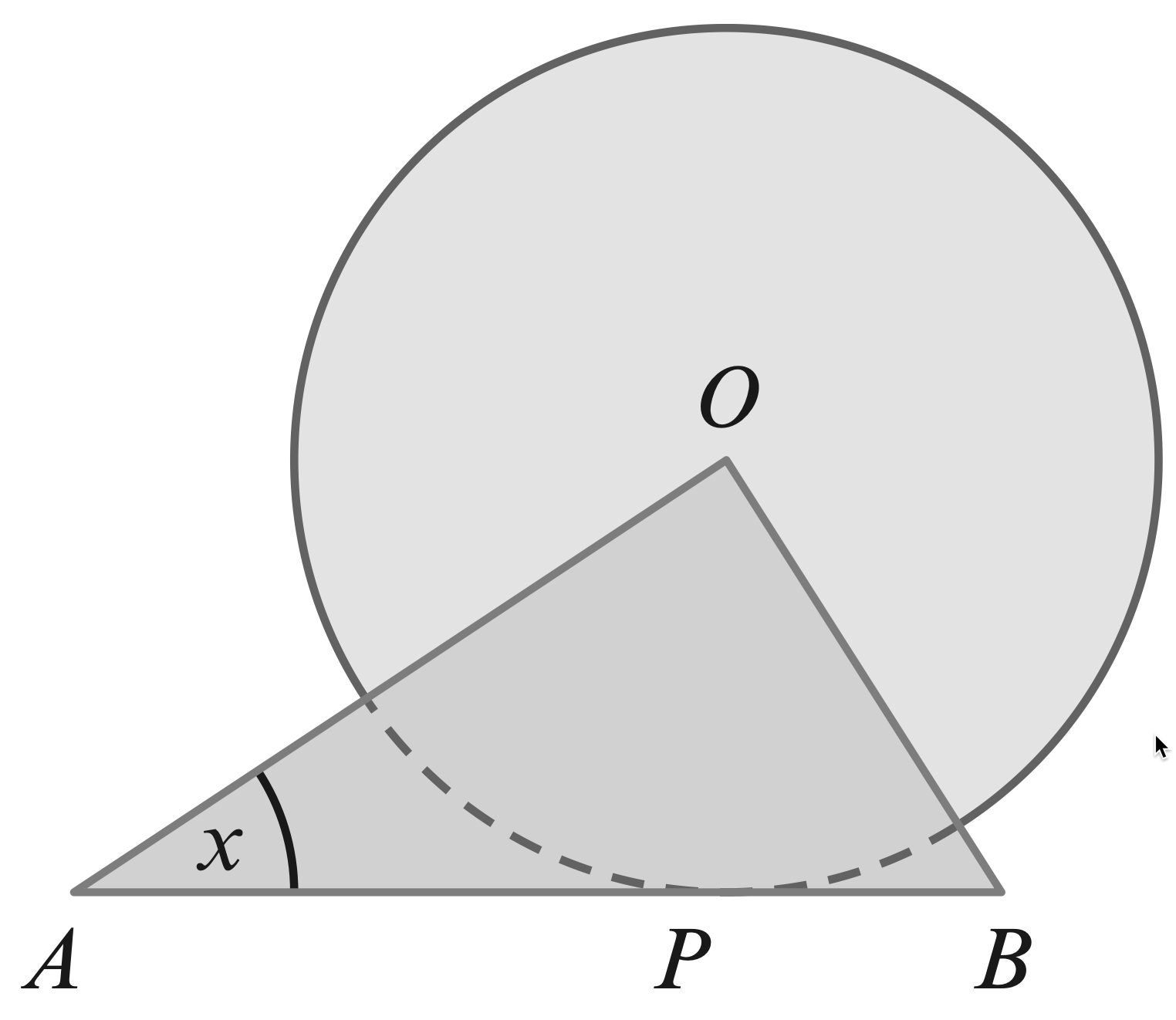
- The diagram shows a circle with radius $1$ cm, centre $O$.
Triangle AOB is right angled and its hypotenuse AB is a tangent
to the circle at $P$. Angle $BAO = x$ radians.
(a) Find an expression for the length of AB in terms of $\tan x$.
(b) Find the value of $x$ for which the two shaded areas are equal.
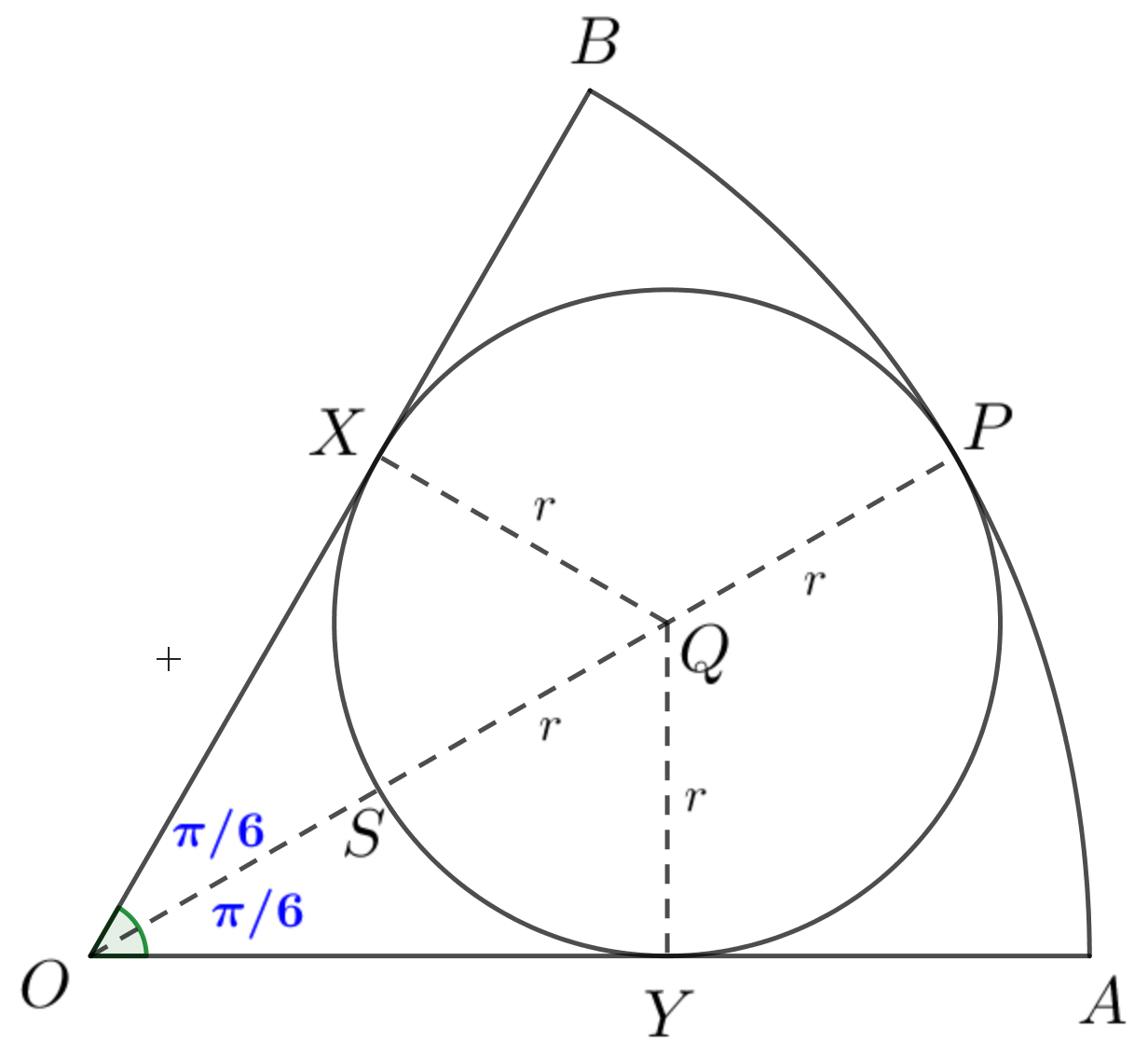
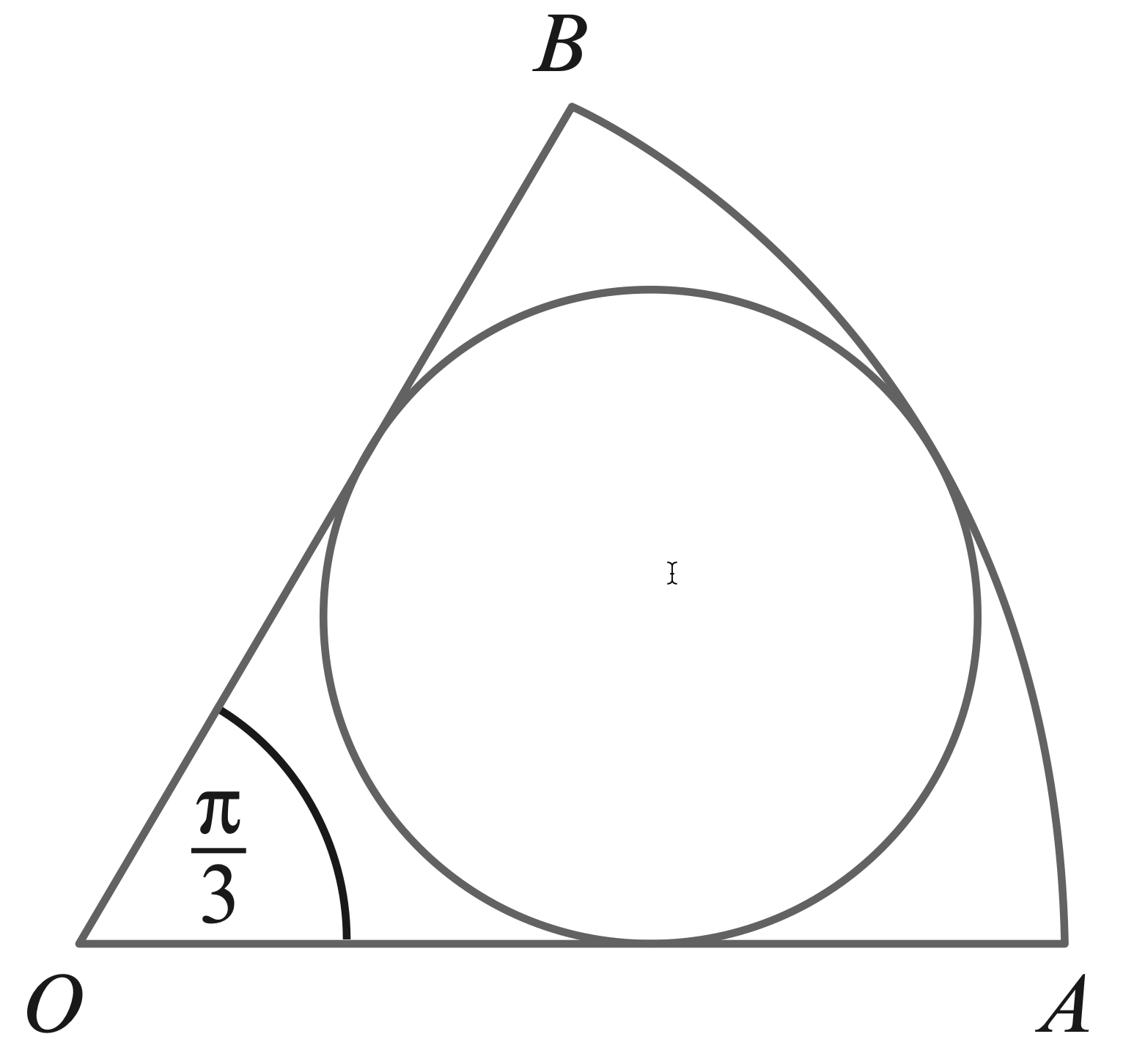
- The diagram shows a sector, $AOB$, of a circle, centre $O$, with radius $R$ cm
and sector angle $\dfrac{π}{3}$ radians.
An inner circle of radius $r$ cm touches the three sides of the sector.
(a) Show that $R = 3r$.
(b) Show that $\dfrac{\text{area of inner circle}}{\text{area of sector}}=\dfrac{2}{3}$ .
- The diagram shows a metal plate made by fixing together two pieces,
$OABCD$ (shaded) and $OAED$ (unshaded). The piece $OABCD$ is a minor sector of
a circle with centre $O $and radius $2r$. The piece $OAED$ is a major sector of
a circle with centre $O$ and radius $r$. Angle $AOD$ is $\alpha$ radians.
Simplifying your answers where possible, find, in terms of $\alpha, \pi$ and $r$,
(a) the perimeter of the metal plate,
(b) the area of the metal plate.
It is now given that the shaded and unshaded pieces are equal in area.
(c) Find $\alpha$ in terms of $\pi$.
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!