Find the equation of the line passing through the vertices of this curve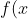=%5Cfrac%7B-2x-9%7D%7Bx+5%7D) .
.
Solution
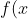=%5Cfrac%7B-2x-9%7D%7Bx+5%7D)
Solution
Let the vertices be  and
and  where
where  .
.
∴&space;&space;%5Cfrac%7B-2a-9%7D%7Ba+5%7D) and
and &space;&space;%5Cfrac%7B-2b-9%7D%7Bb+5%7D)
The gradient of tangent to the curve is&space;=%5Cfrac%7B1%7D%7B%7B%7B(x+5)%7D%5E%7B2%7D%7D%7D.)
At vertices, the tangents are parallel.
∴





Since .
.
 and
and  .
.

Since the line passing through vertices is perpendicular to the respective tangents, its gradient is .
.
Hence




 (or)
(or) 
 (or)
(or) 
 (or)
(or)  and
and
 (or)
(or) 
Therefore, the vertices are (– 4, – 1) and (– 6, – 3).
Hence the equation of required line is

 (or)
(or) 
∴
The gradient of tangent to the curve is
At vertices, the tangents are parallel.
∴
Since
Since the line passing through vertices is perpendicular to the respective tangents, its gradient is
Hence
Therefore, the vertices are (– 4, – 1) and (– 6, – 3).
Hence the equation of required line is
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!



