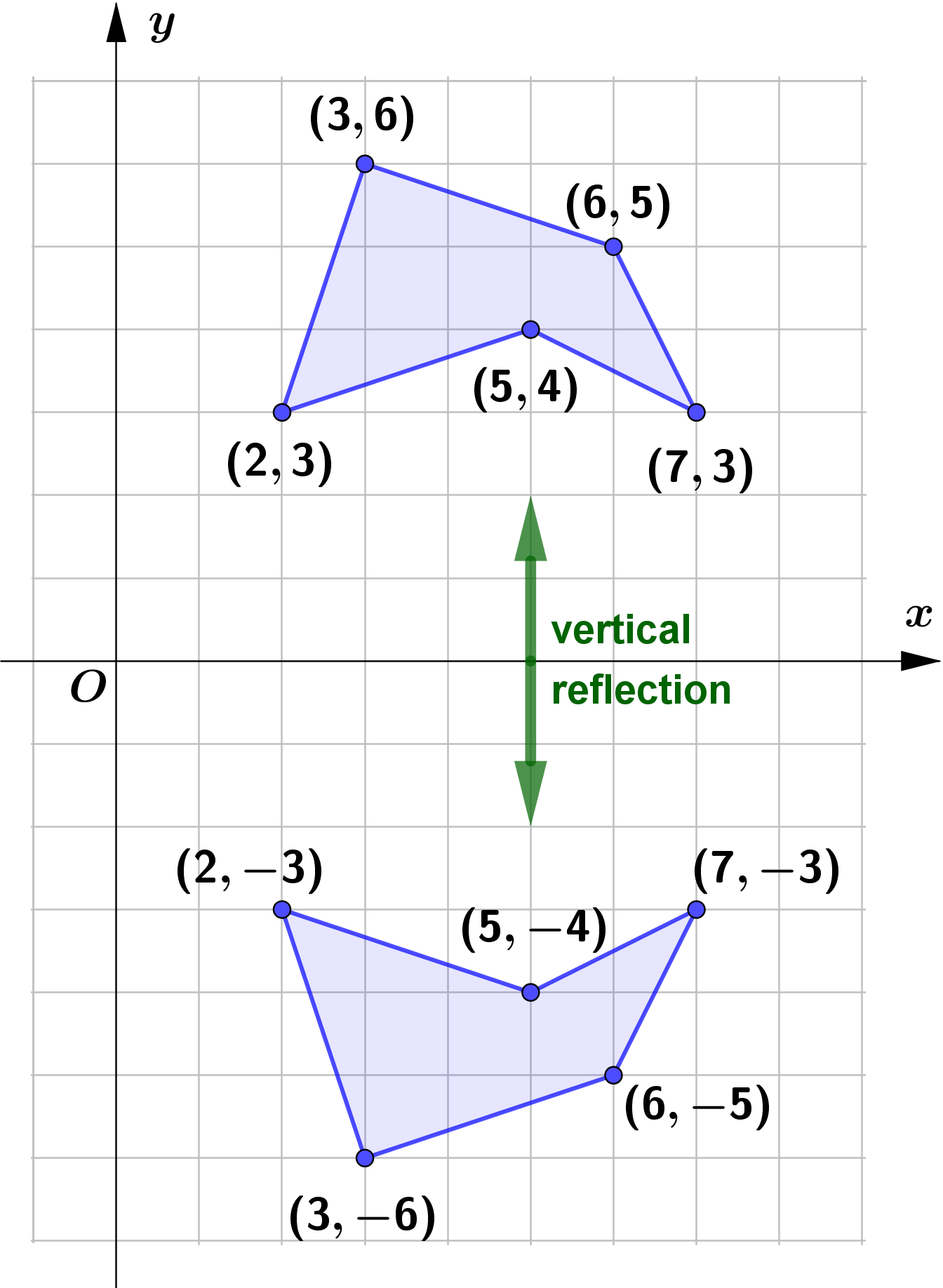
Vertical Reflection (Reflection about $x$-axis)
Given a function $f(x)$, a new function $g(x)=-f(x)$
is a horizontal reflection (reflection about the $x$-axis) of the function.
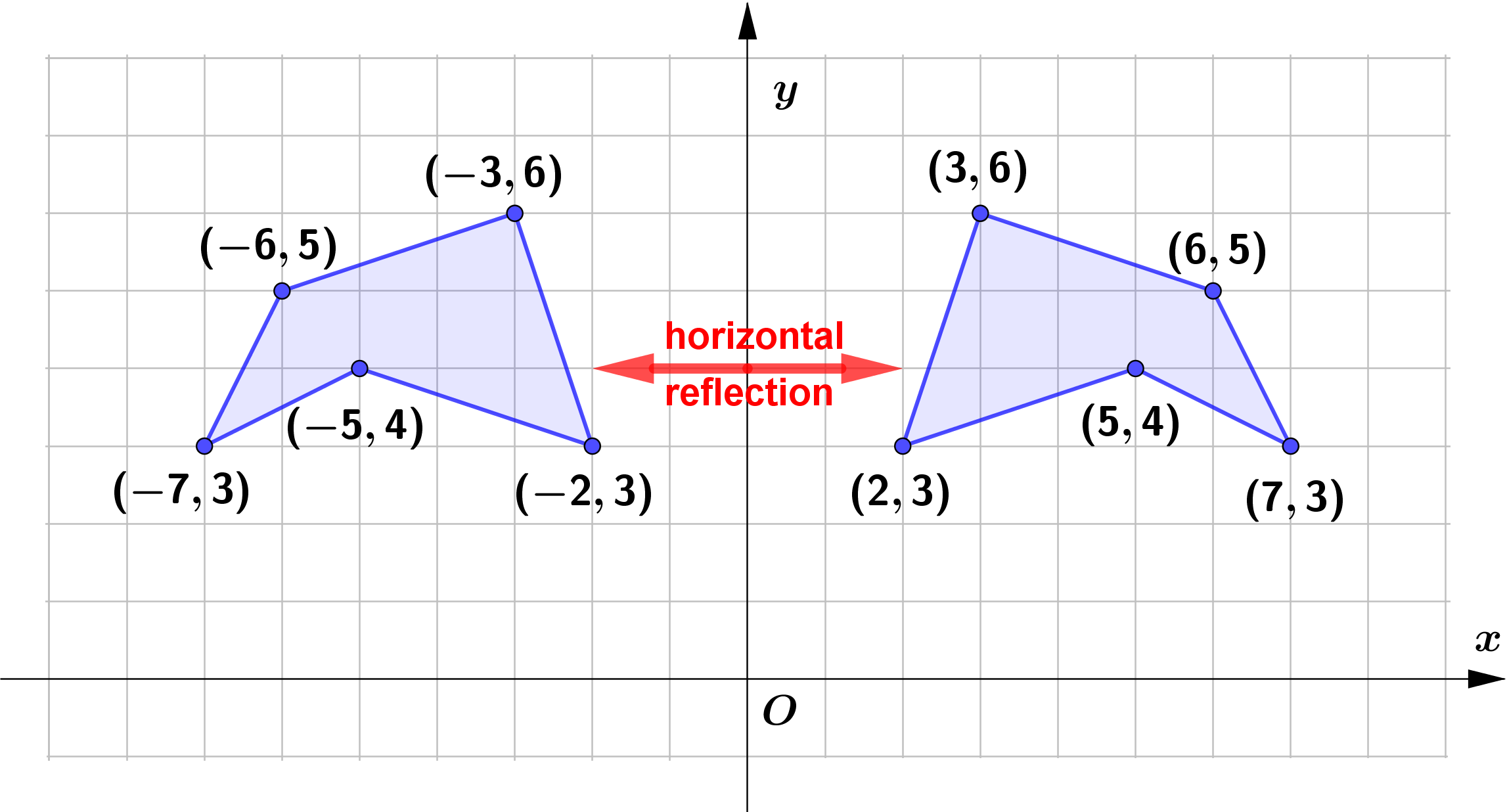
Horizontal Reflection (Reflection about $y$-axis)
Given a function $f(x)$, a new function $g(x)=-f(x)$
is a horizontal reflection (reflection about the $y$-axis) of the function.
Question (1)
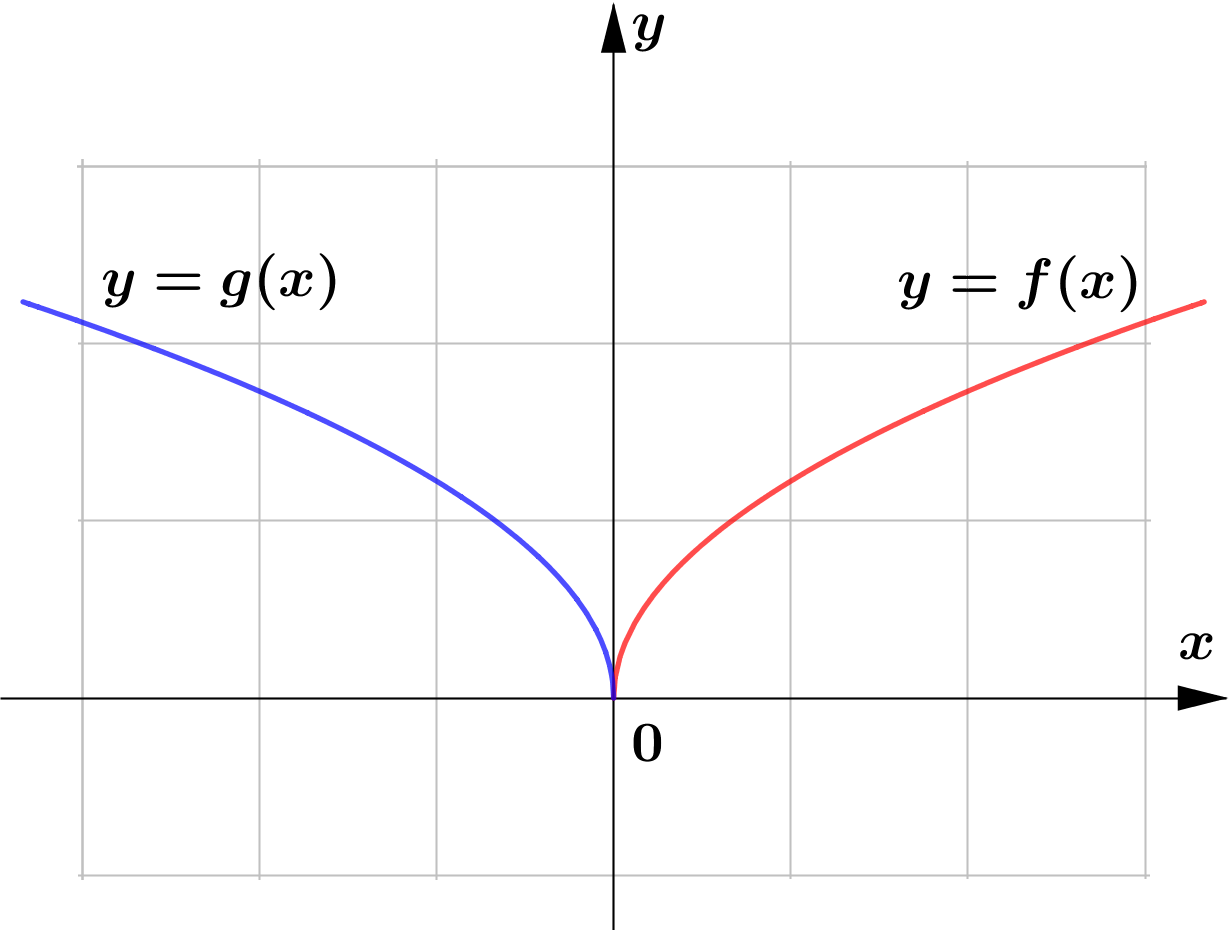
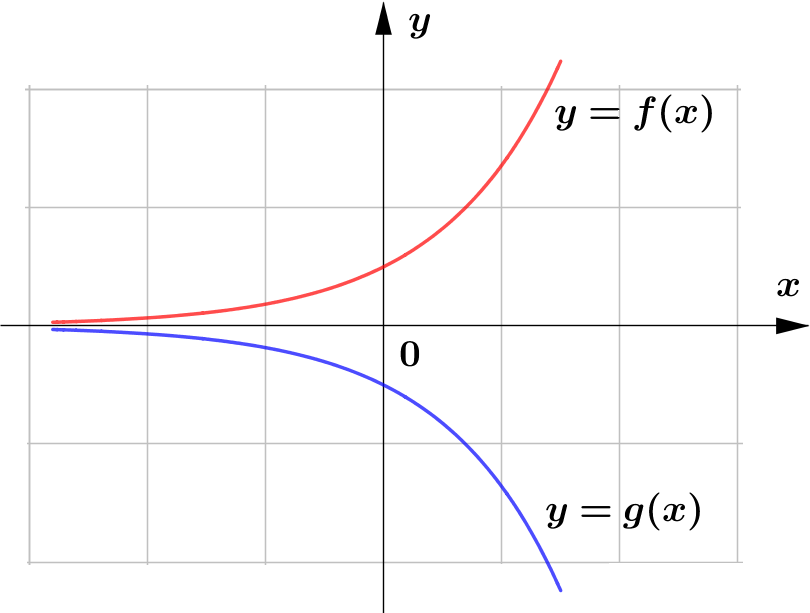
The following are the sketch of the graphs of $y=f(x)$ and $y=g(x)$. Determine whether the graphs of $y=g(x)$ represents horizontal or vertical reflection of that of $y=f(x)$.
(a)
(b)
(c)
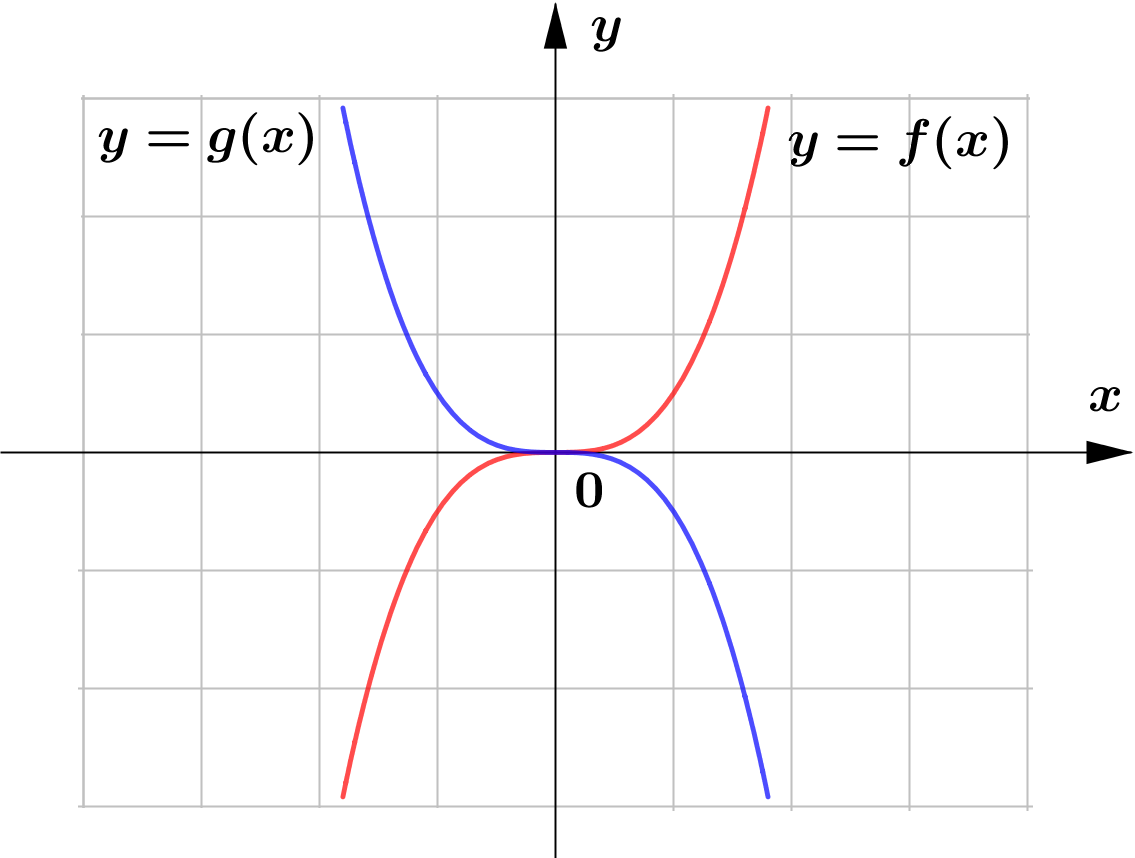
(d)
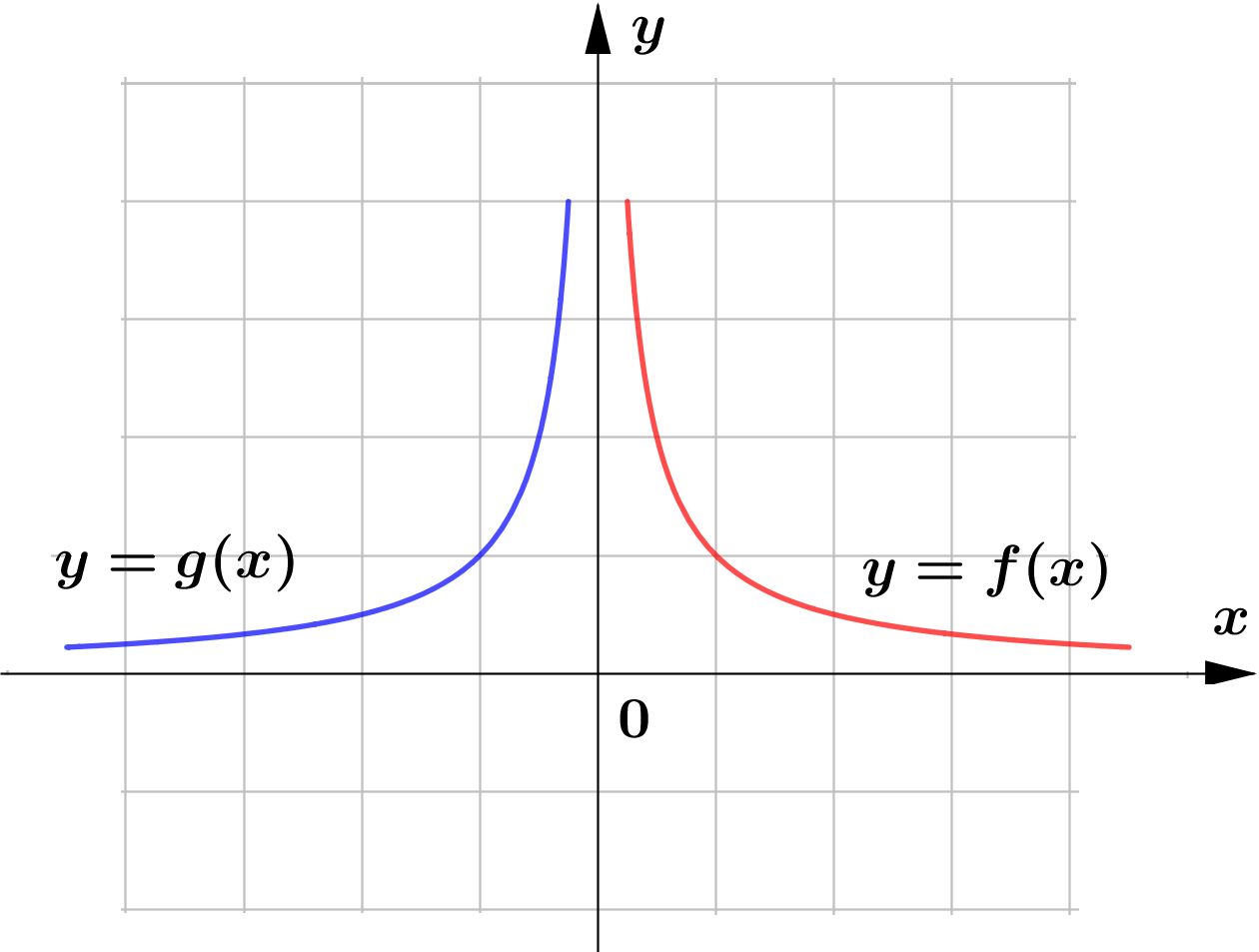
(e)
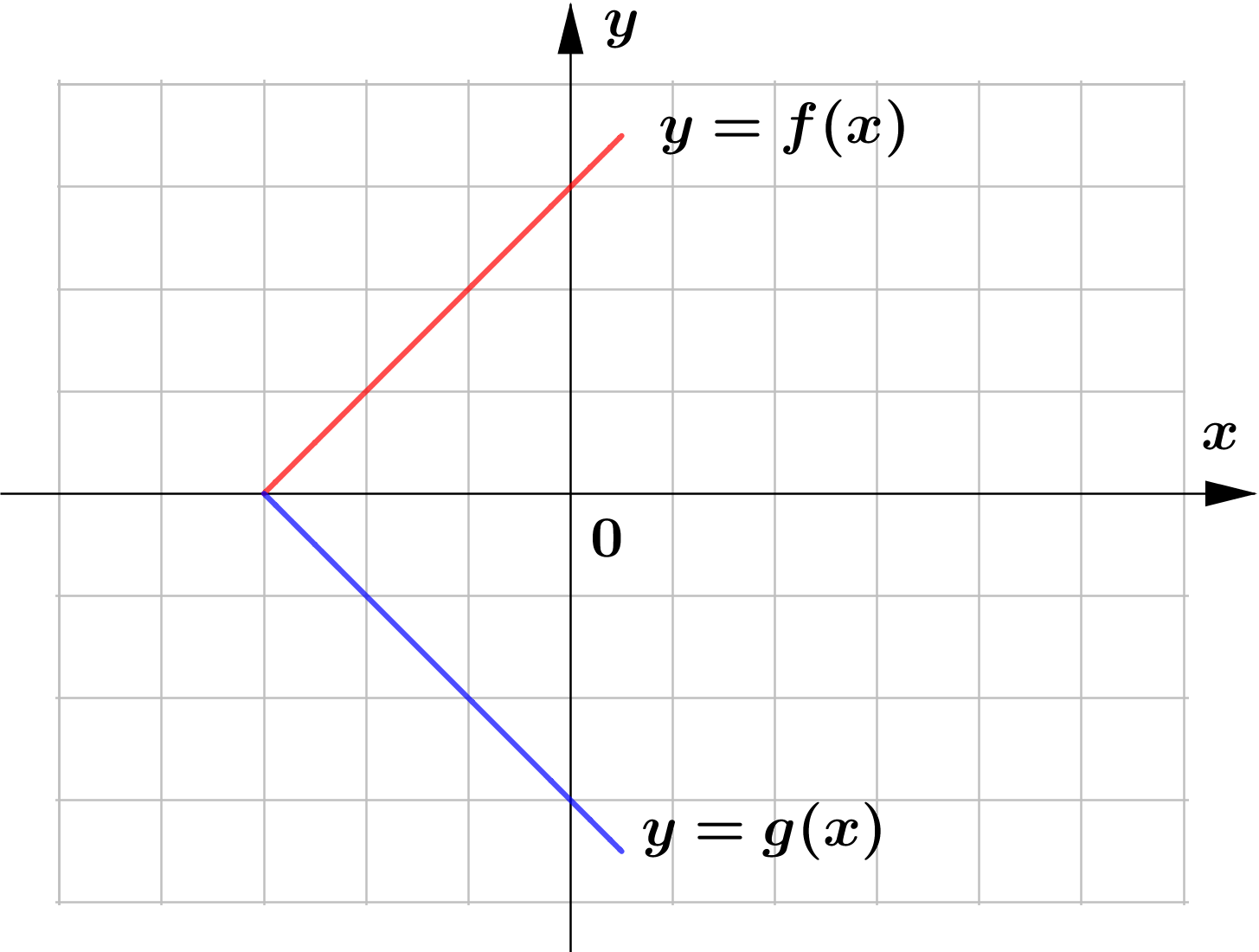
(f)
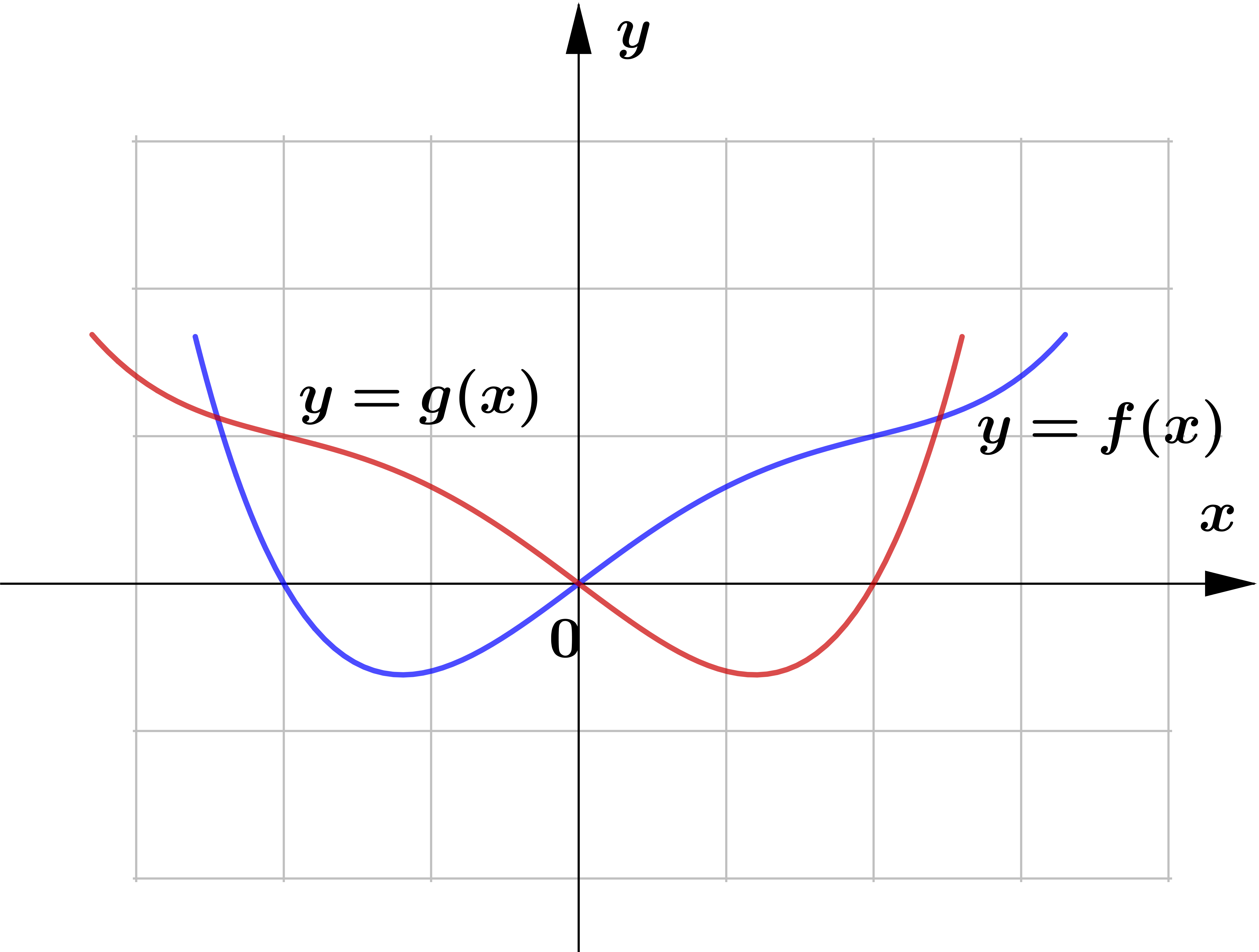
Question (2)
Assume that $(a, b)$ is a point on the graph of $y=f(x)$.
What is the corresponding point on the graph of each
of the following functions?
$\begin{array}{l}
\text{(a) } y=f(-x)\\\\
\text{(b) } y=-f(x)\\\\
\text{(c) } y=f(3-x)\\\\
\text{(d) } y=f(-x)-3
\end{array}$
Question (3)
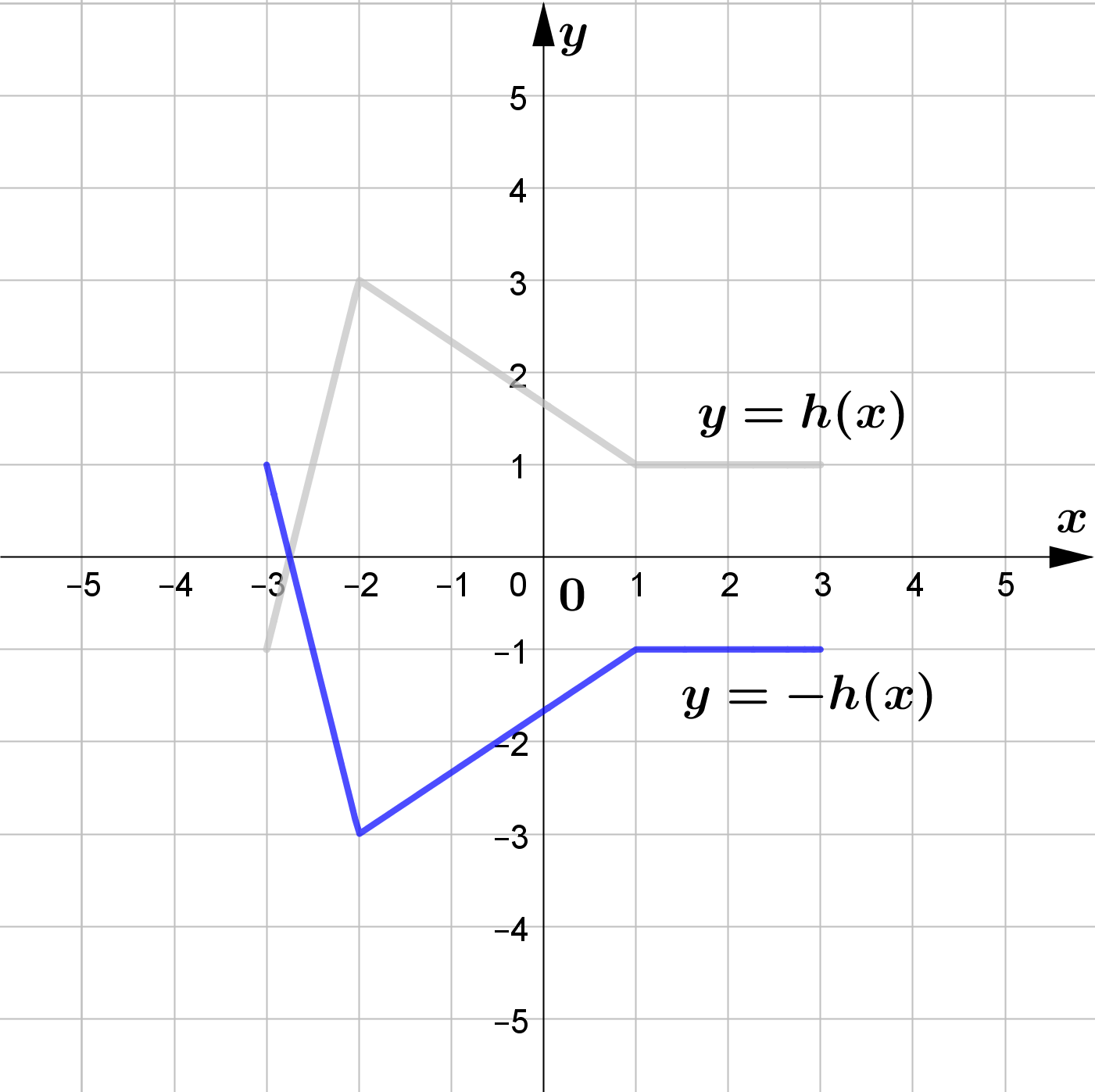
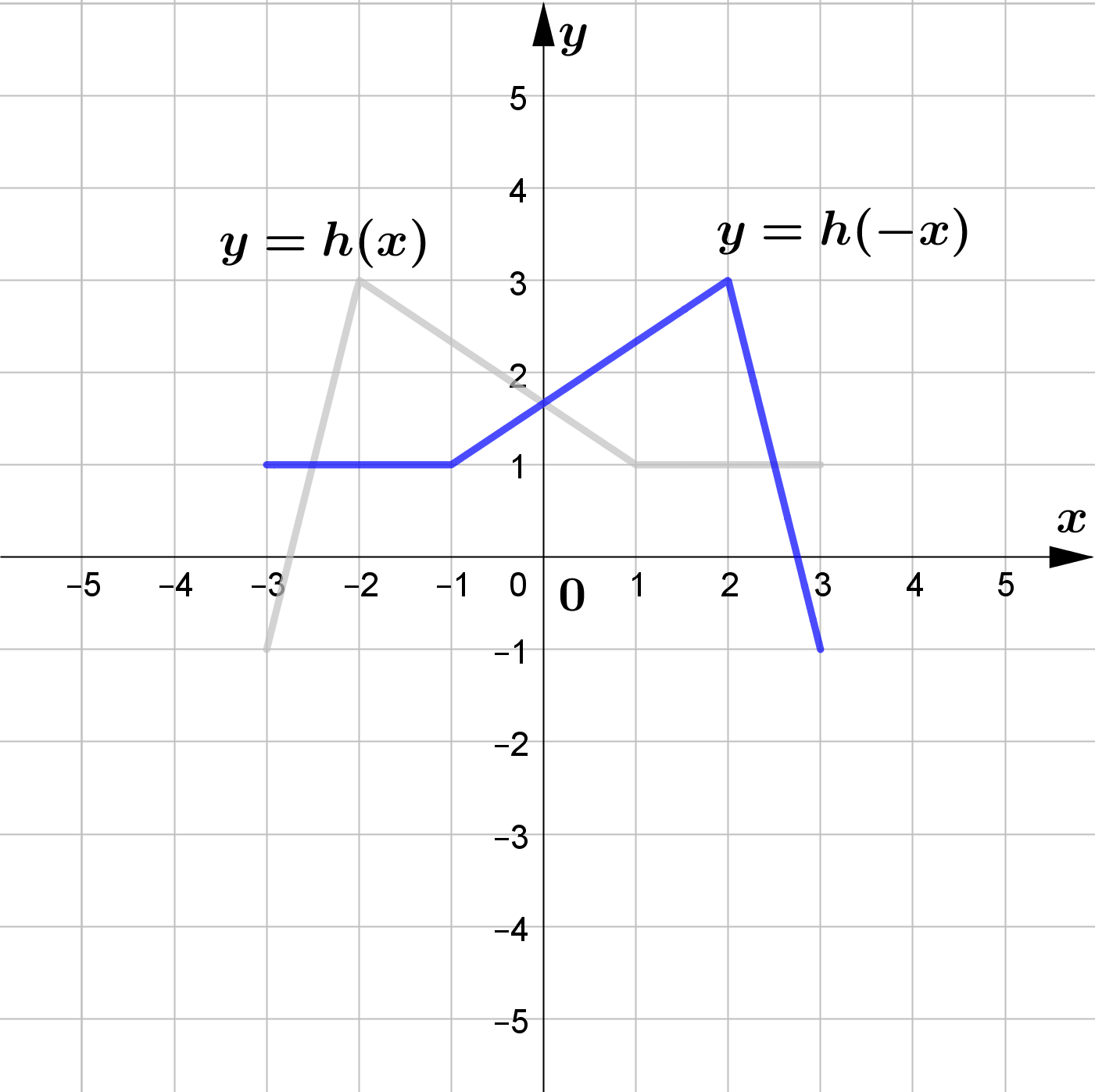
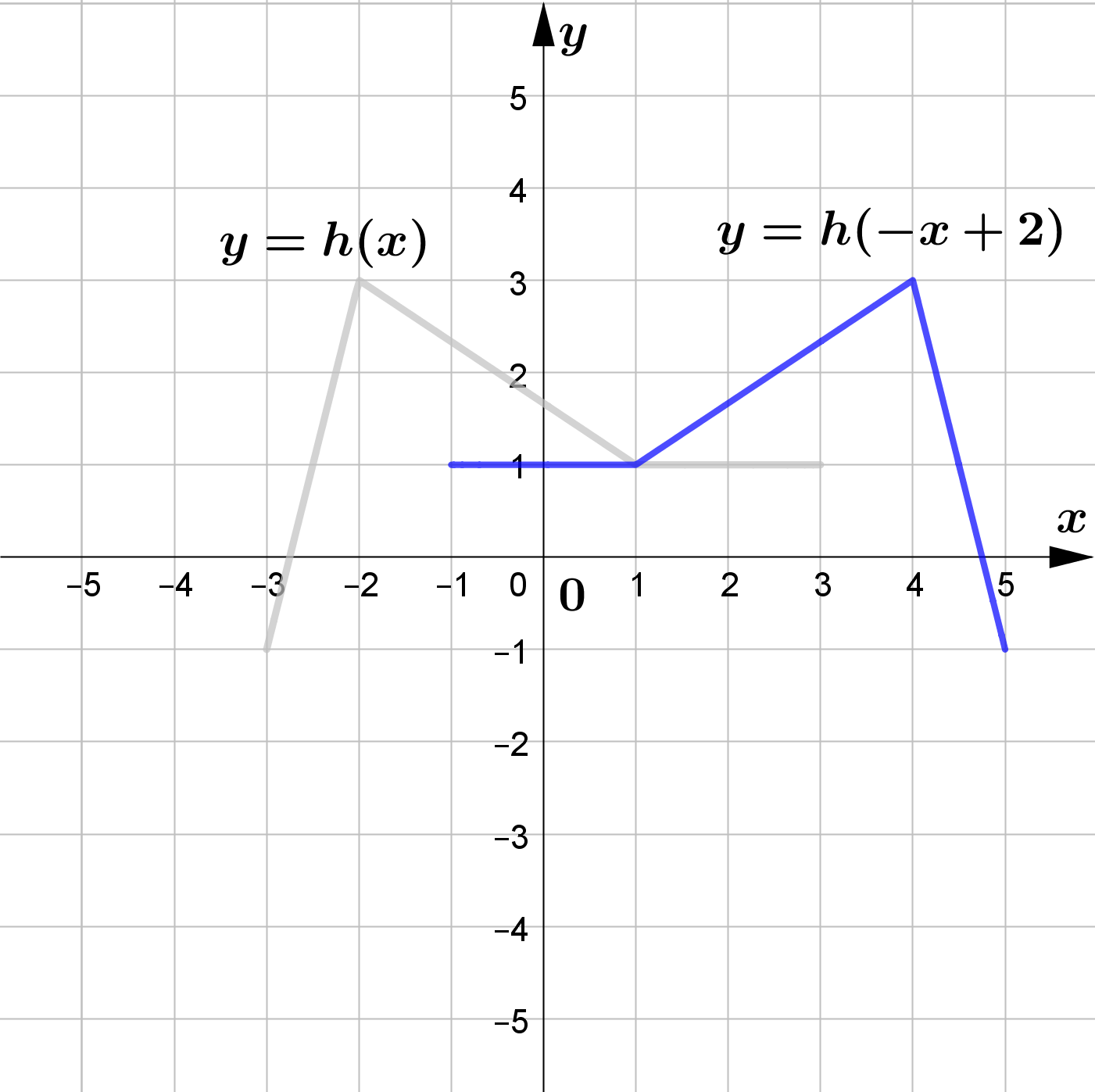
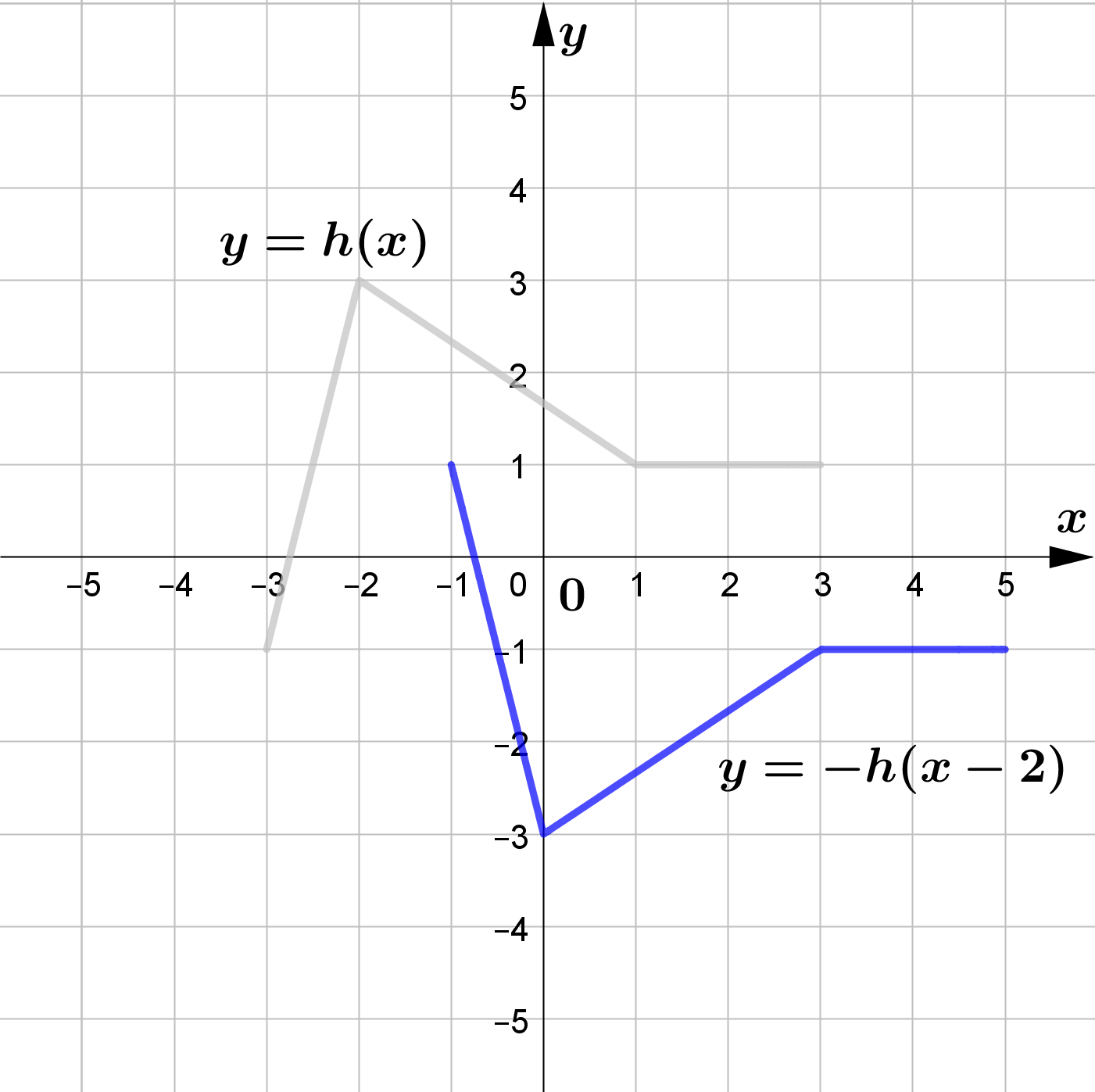
The figure shows the graph of $y=h(x)$.
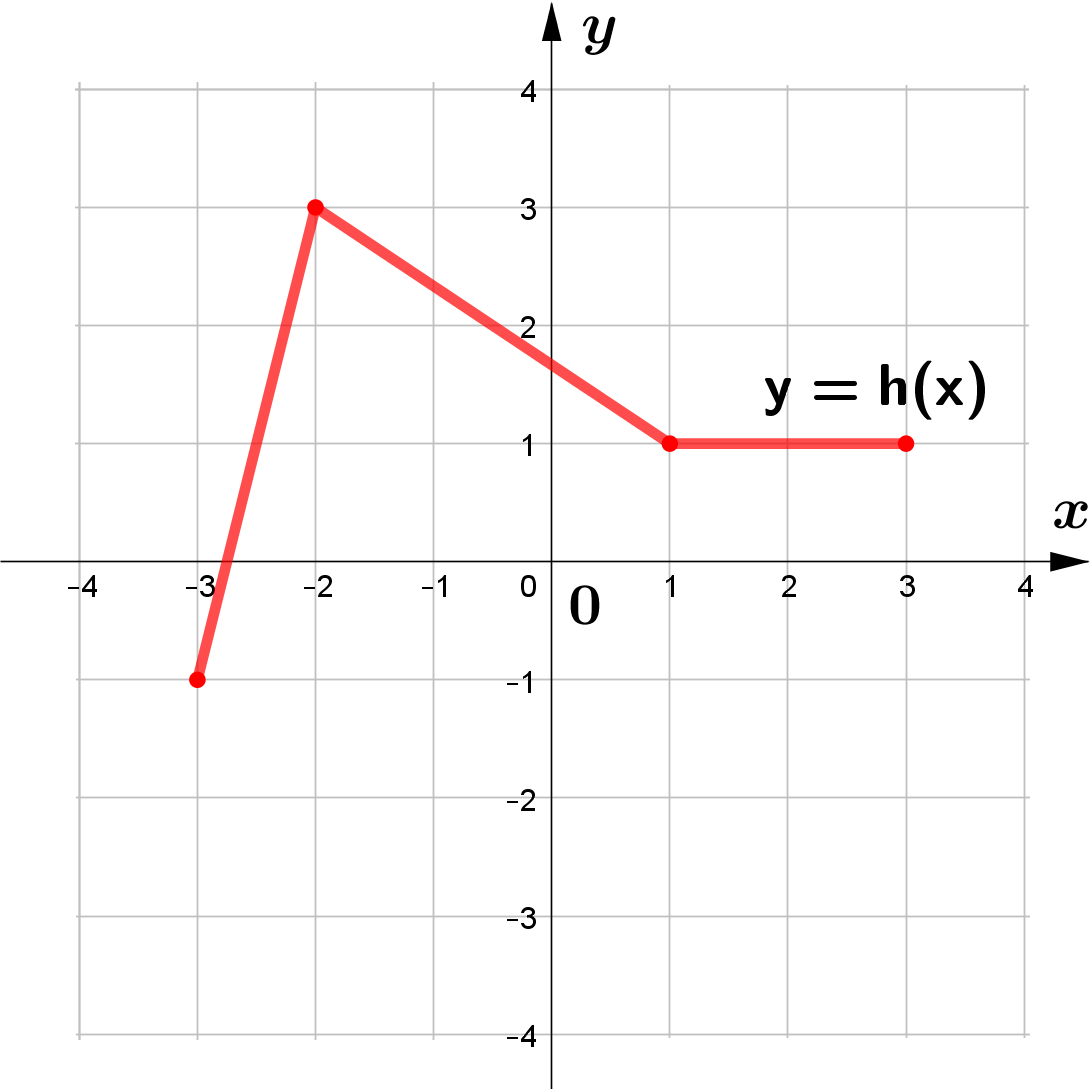
Sketch the graphs of each of the following functions.
$\begin{array}{l}
\text{(a) } y=-h(x)\\\\
\text{(b) } y=h(-x)\\\\
\text{(c) } y=h(-x)+2\\\\
\text{(d) } h(x-2)
\end{array}$
Question (4)
If $g$ is obtained from $f$ through a sequence of transformations, find an equation for $g$.
(a)
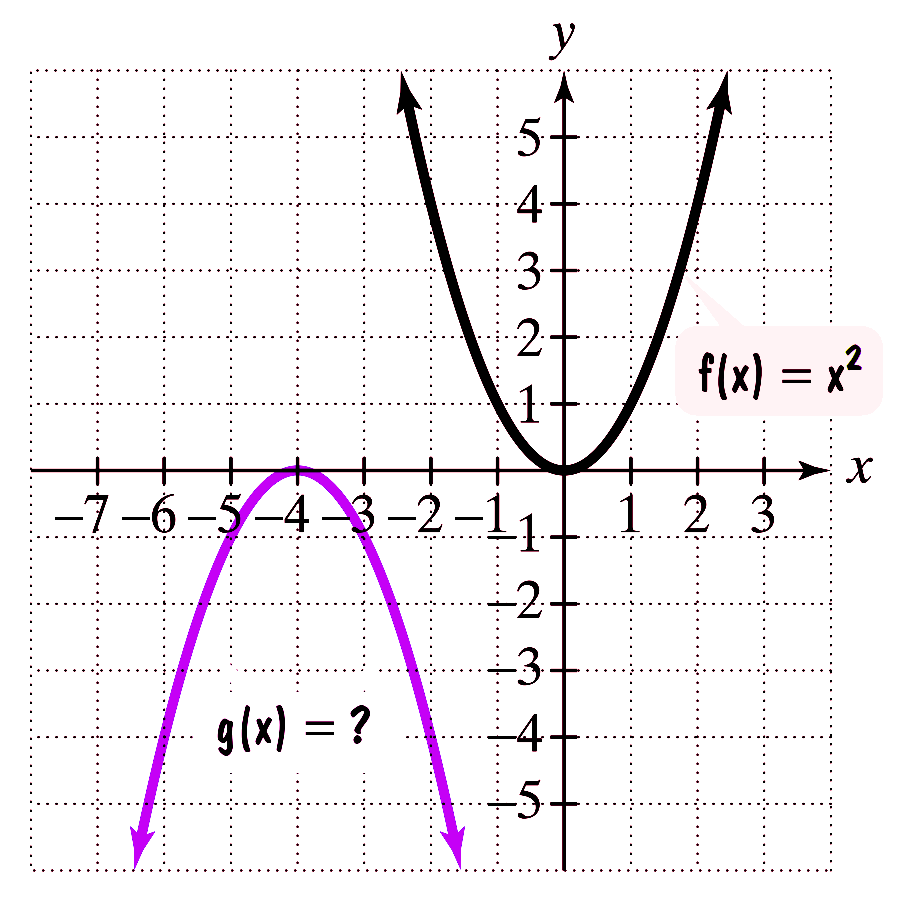
(b)
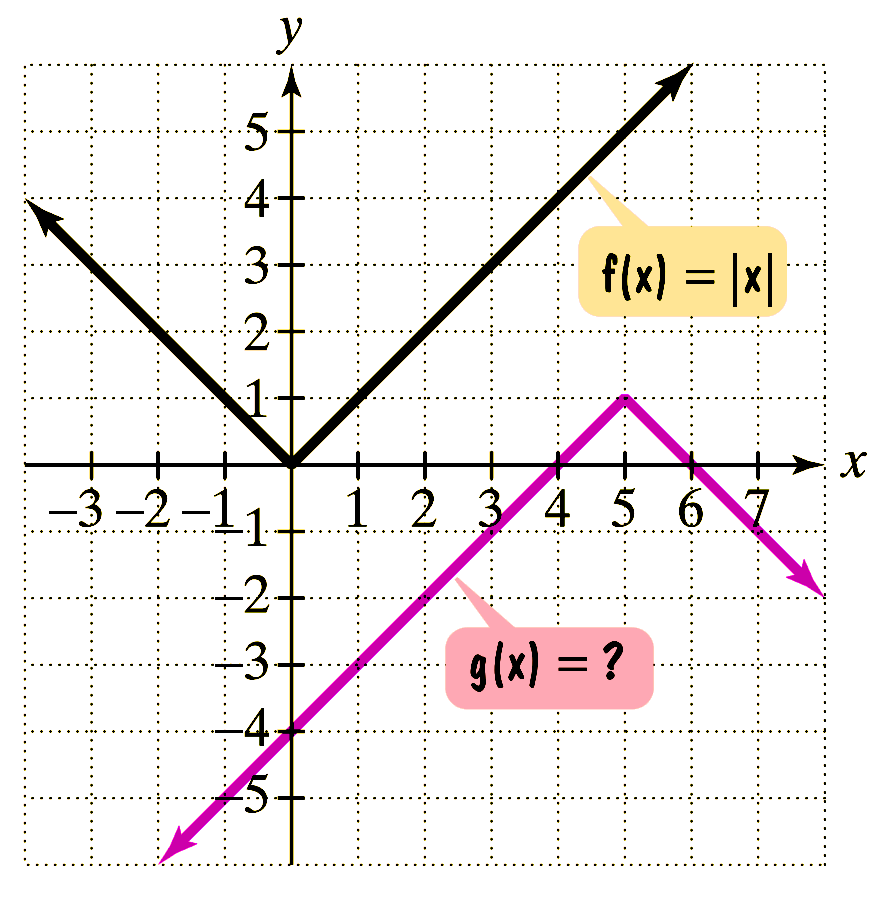
Question (5)
Which of the following is true?
| $\text{(a)}$ | If $f(x)=|x|$ and $g(x)=|x+3|+3$, then the graph of $g$ is a translation of three units to the right and three units upward of the graph of $f$. |
| $\text{(b)}$ | If $f(x)=-\sqrt{x}$ and $g(x)=\sqrt{-x}$, then $f$ and $g$ have identical graphs. |
| $\text{(c)}$ | If $f(x)=x^{2}$ and $g(x)=-\left(x^{2}-2\right)$, then the graph of $g$ can be obtained from the graph of $f$ by a downward shift of two units and then reflecting in the $x$-axis. |
| $\text{(d)}$ | If $f(x)=x^{3}$ and $g(x)=-(x-3)^{3}-4$, then the graph of $g$ can be obtained from the graph of $f$ by moving $f$ three units to the right, reflecting in the $x$-axis, and then moving the resulting graph down four units. |