Vertical Stretches and Compressions
Given a function $f(x)$, a new function $g(x)=c f(x)$, where $c$ is a positive constant, is a vertical stretch or vertical compression (parallel to the $y$-axis) of the function $f(x)$ with a scale factor $c$.
- If $c>1$, then the graph will be stretched.
- If $0< c< 1$, then the graph will be compressed.
Horizontal Stretches and Compressions
Given a function $f(x)$, a new function $g(x)= f(cx)$, where $c$ is a positive constant, is a horizontal stretch or horizontal compression (parallel to the $x$-axis) of the function $f(x)$ with a scale factor $\frac{1}{c}$.
- If $c>1$, then the graph will be compressed by $\dfrac{1}{c}$.
- If $0< c< 1$, then the graph will be stretched $\dfrac{1}{c}$.
Question 1
The point $P(3, -2)$ lies on the graph $y=f(x)$.
State the coordinates of the map of the point $P$ on each of the following graph .
$\begin{array}{l}
\\
\text{(a) } y=f(2x)\\\\
\text{(b) } y=f(2x-1) \\\\
\text{(c) } y= f(2x-1) -3\\\\
\text{(d) } y=3f(x)\\\\
\text{(e) } y=-3f(x)\\\\
\text{(f) } y=-3f(-x)\\\\
\end{array}$
Question 2
The point $P(-1, 3)$ lies on the graph $y=f(x)$. State the coordinates of the map of the point $P$ on each of the following graph .
| $ \text{(a)}$ | On the graph of $y=a f(x)$, where $a$ is a positive constant, the point $P$ is mapped to the point $(-1,1)$. Determine the value of $a$. |
| $ \text{(b)}$ | On the graph of $y={f}(k x)$, where $k$ is a positive constant, the point $P$ is mapped to the point $(-3,3)$. Determine the value of $k$. |
Question 3
The point $A(a, b)$ lies on the graph $y=f(x)$. State the coordinates of the map
of the point $A$ on each of the following graphs.
$\begin{array}{l}
\\
\text{(a) } y=\dfrac{1}{2}f(x) \\\\
\text{(b) } y=3f(x) + 1 \\\\
\text{(c) } y=f(2x-1)
\end{array}$
Question 4
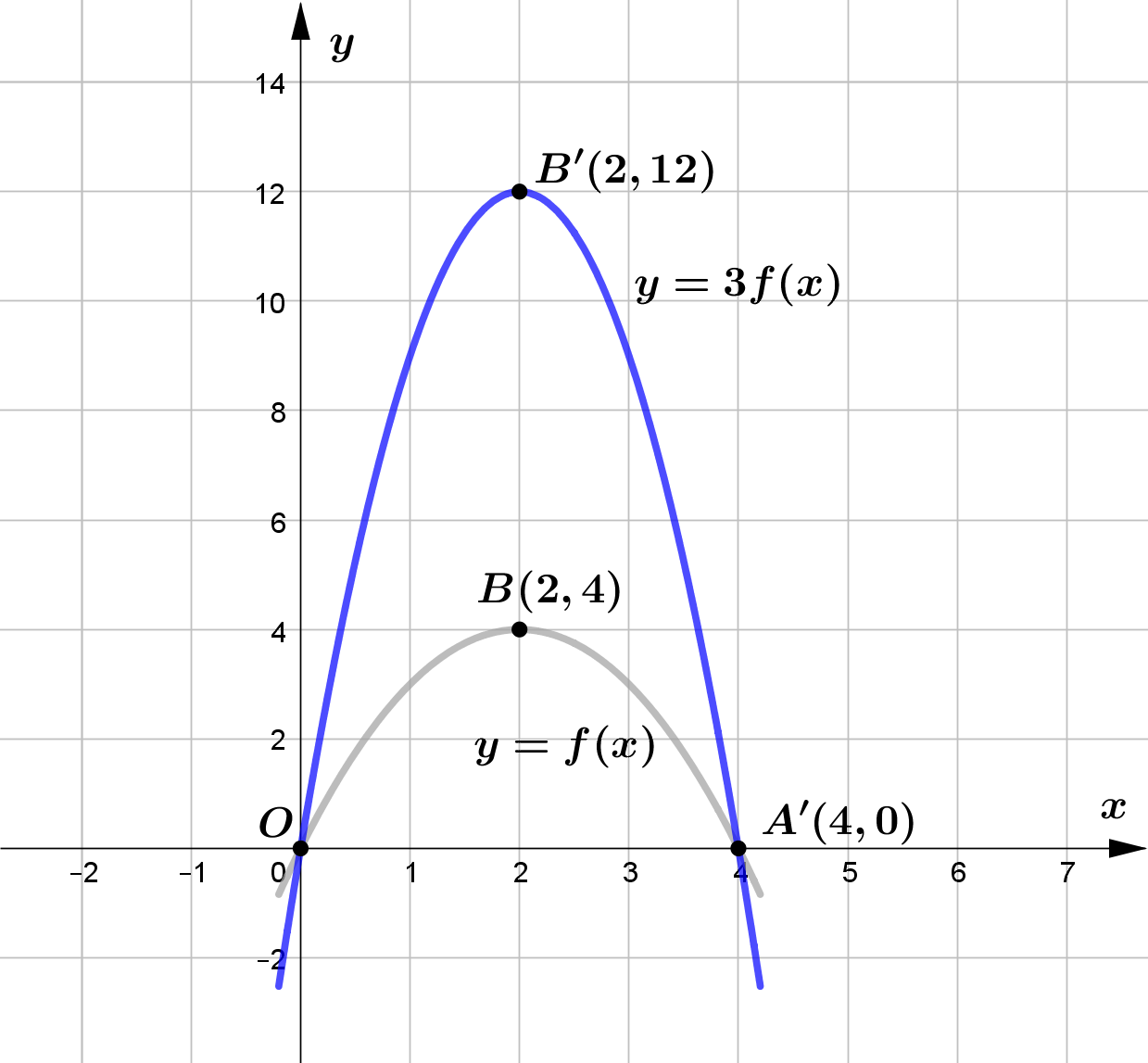
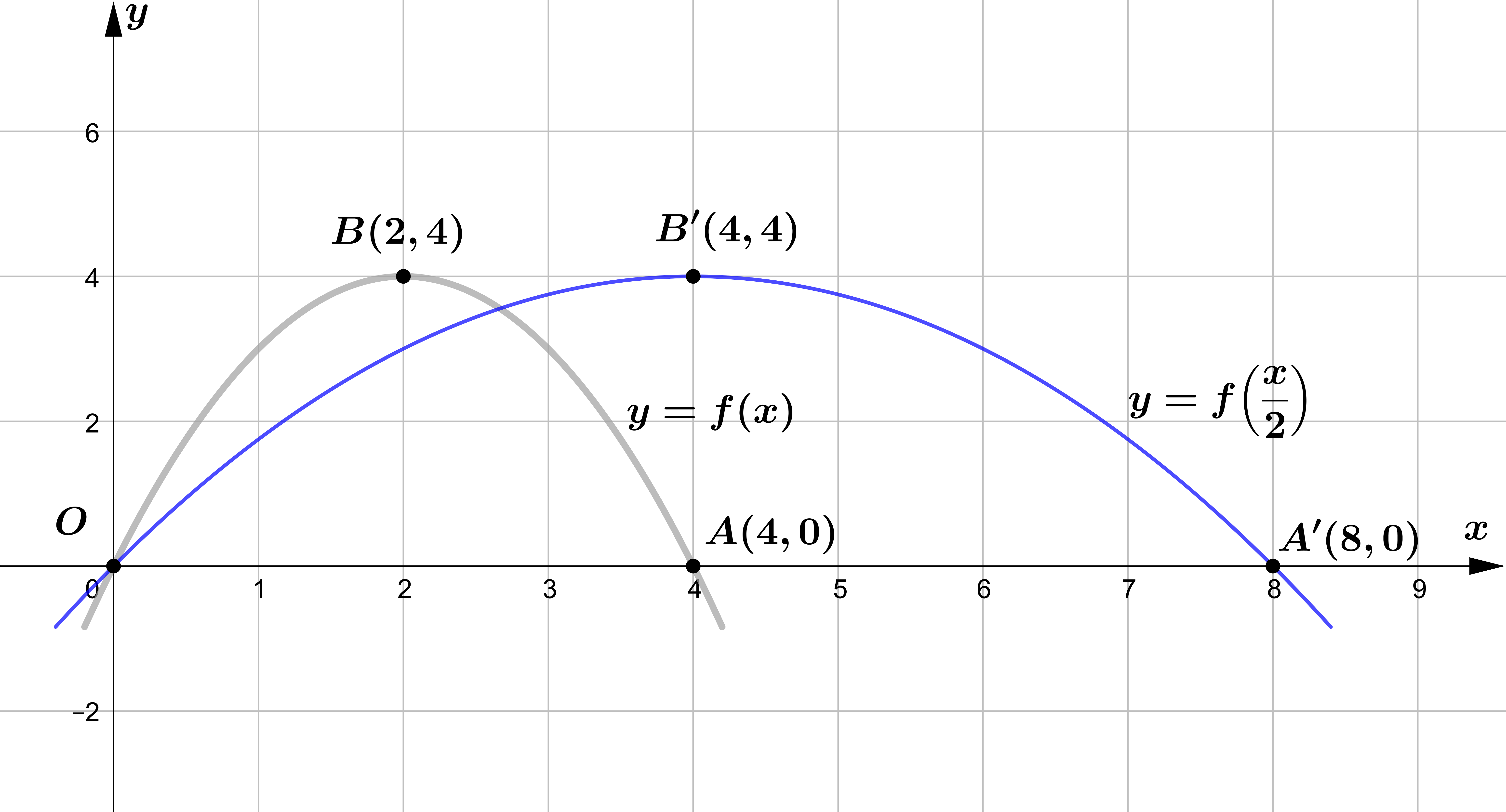
The figure shows the parabola with equation y = f ( x ) with vertex at B( 2,4).
The graph cuts the x axis at O( 0, 0) and at the point A( 4, 0).
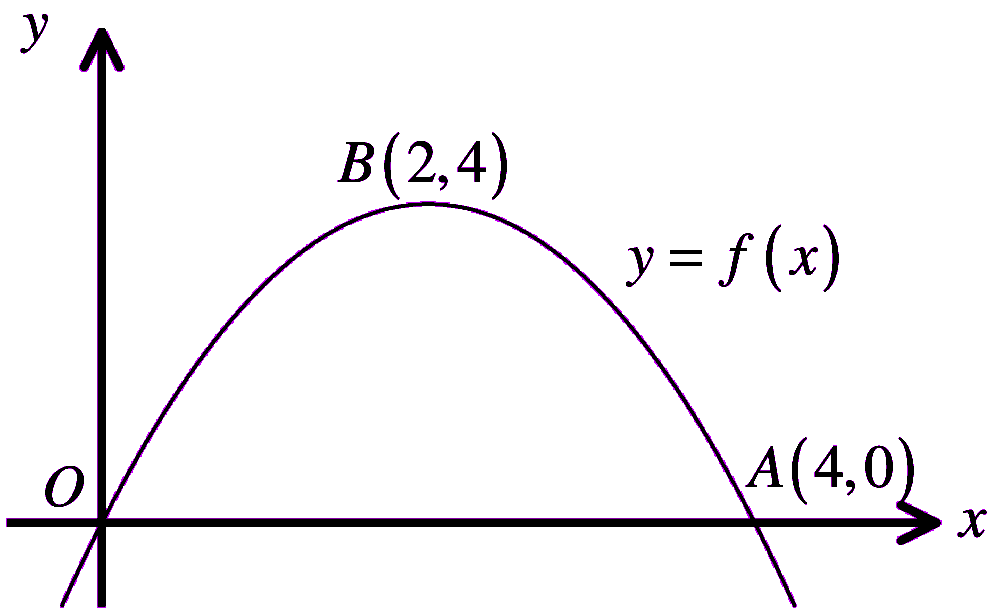
Sketch on a separate set of axes the graph of …
$\begin{aligned}
&\\
&\text{(a) } y=3f(x)\\\\
&\text{(b) } y=f\left(\frac{x}{2}\right)\\\\
\end{aligned}$
Each sketch must include the coordinates of any points where the graph crosses the
coordinate axes and the new coordinates of the vertex of the curve.
Question 5
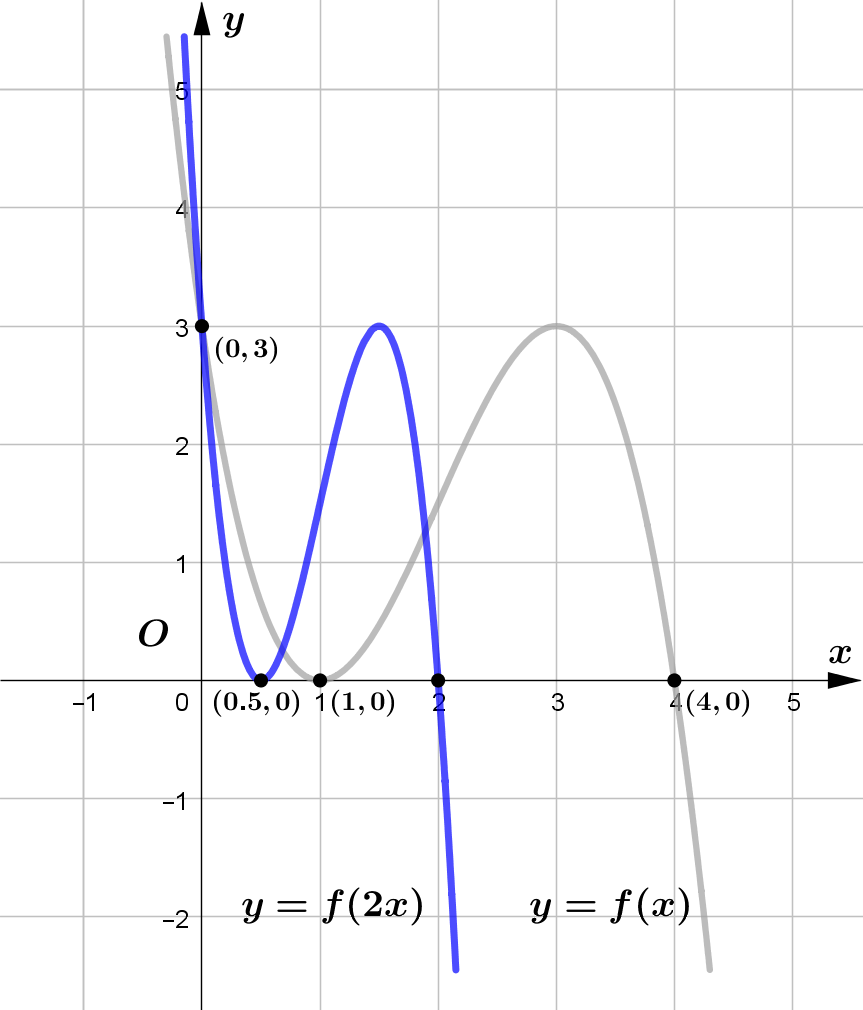
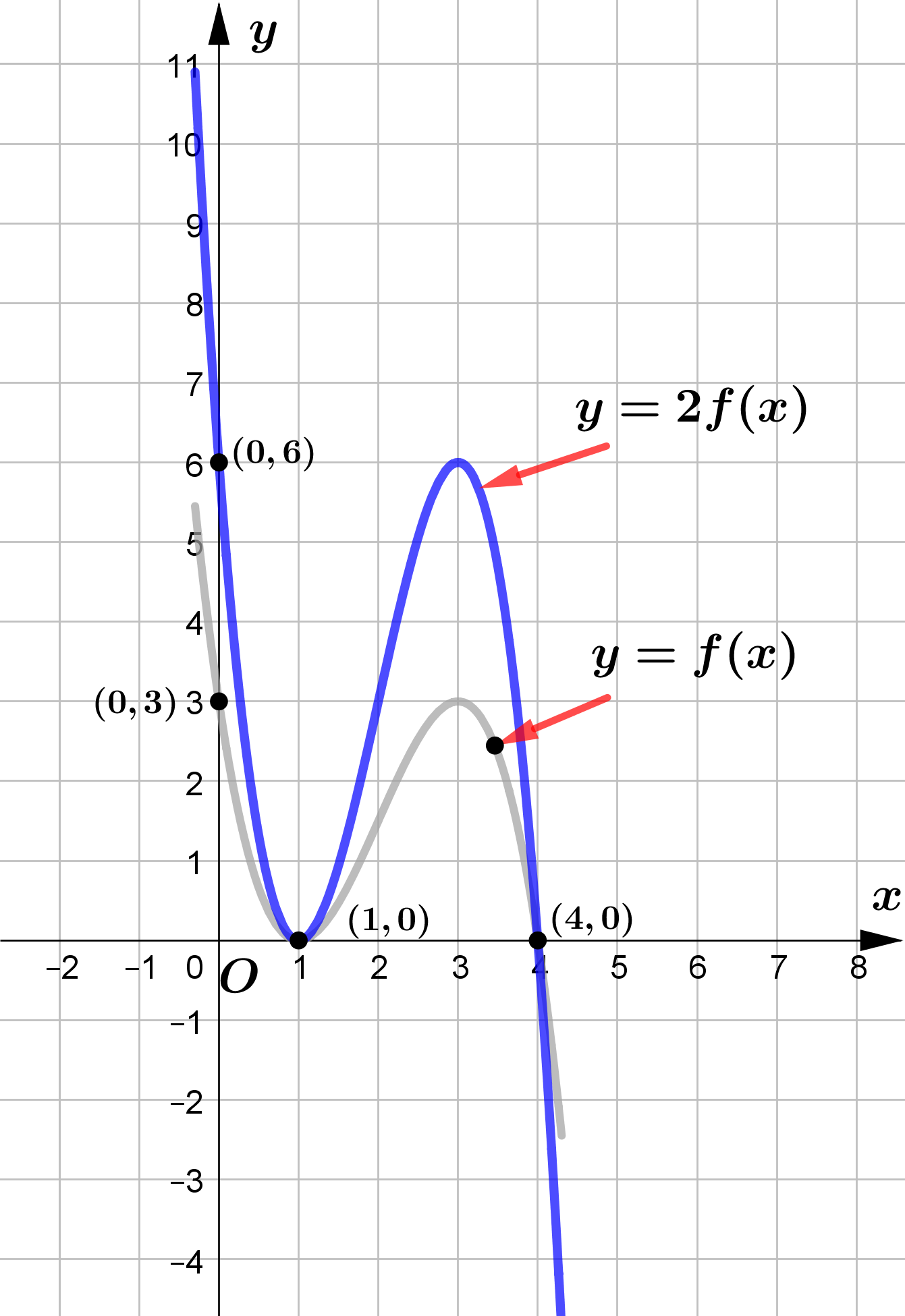
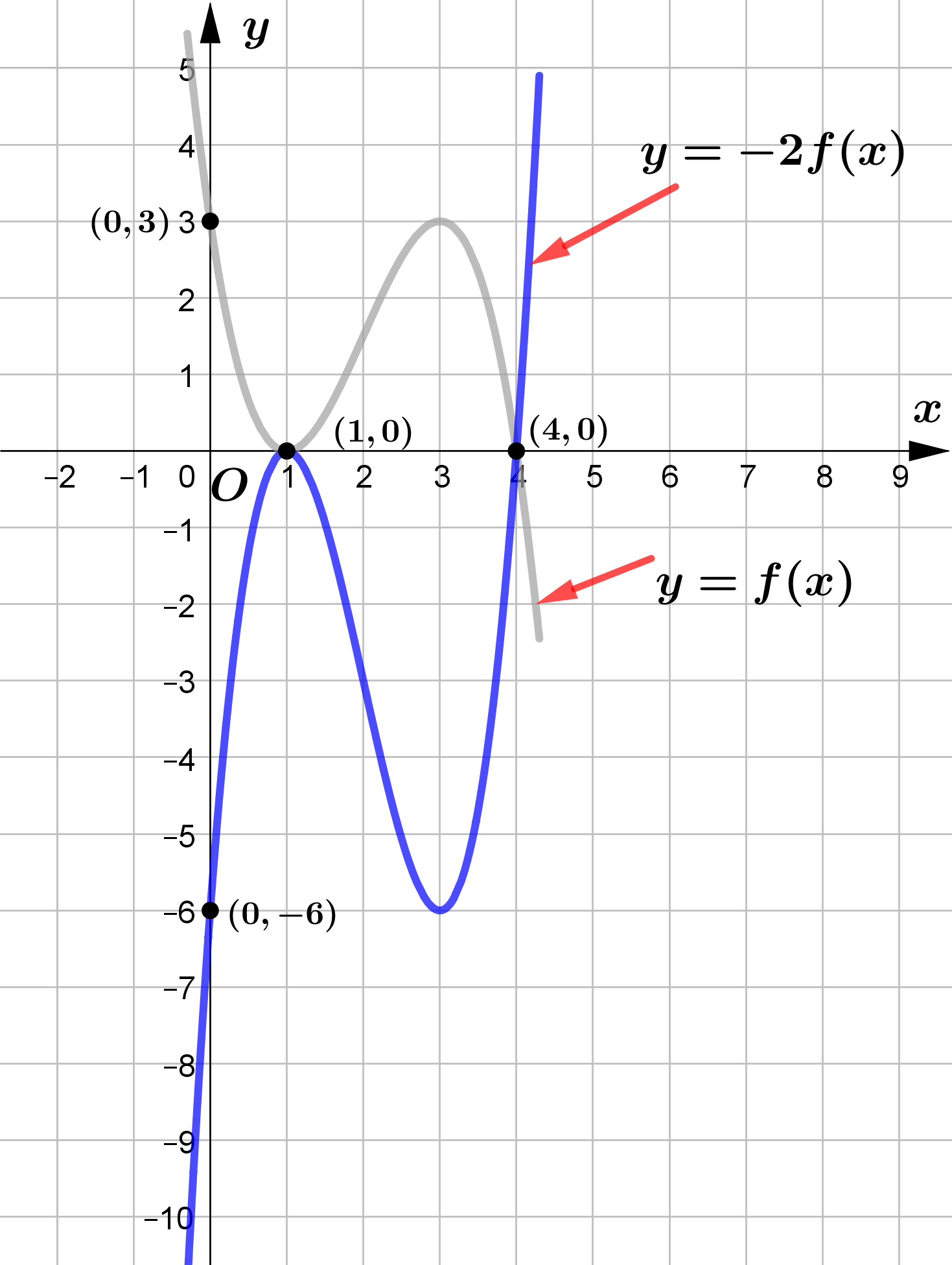
The figure shows a sketch of the curve with equation $y = f(x)$.
The curve passes through the points $(0, 3)$ and $(4, 0)$ and touches
the $x$-axis at the point $(1, 0)$.
On separate diagrams sketch the curve with equation ...
$\begin{aligned}
&\\
&\text{(a) } y = f(2x)\\\\
&\text{(b) } y = 2f(x)\\\\
&\text{(c) } y = -2f(x)\\\\
\end{aligned}$
On each diagram show clearly the coordinates of all the points where the curve meets
the axes.
Question 6
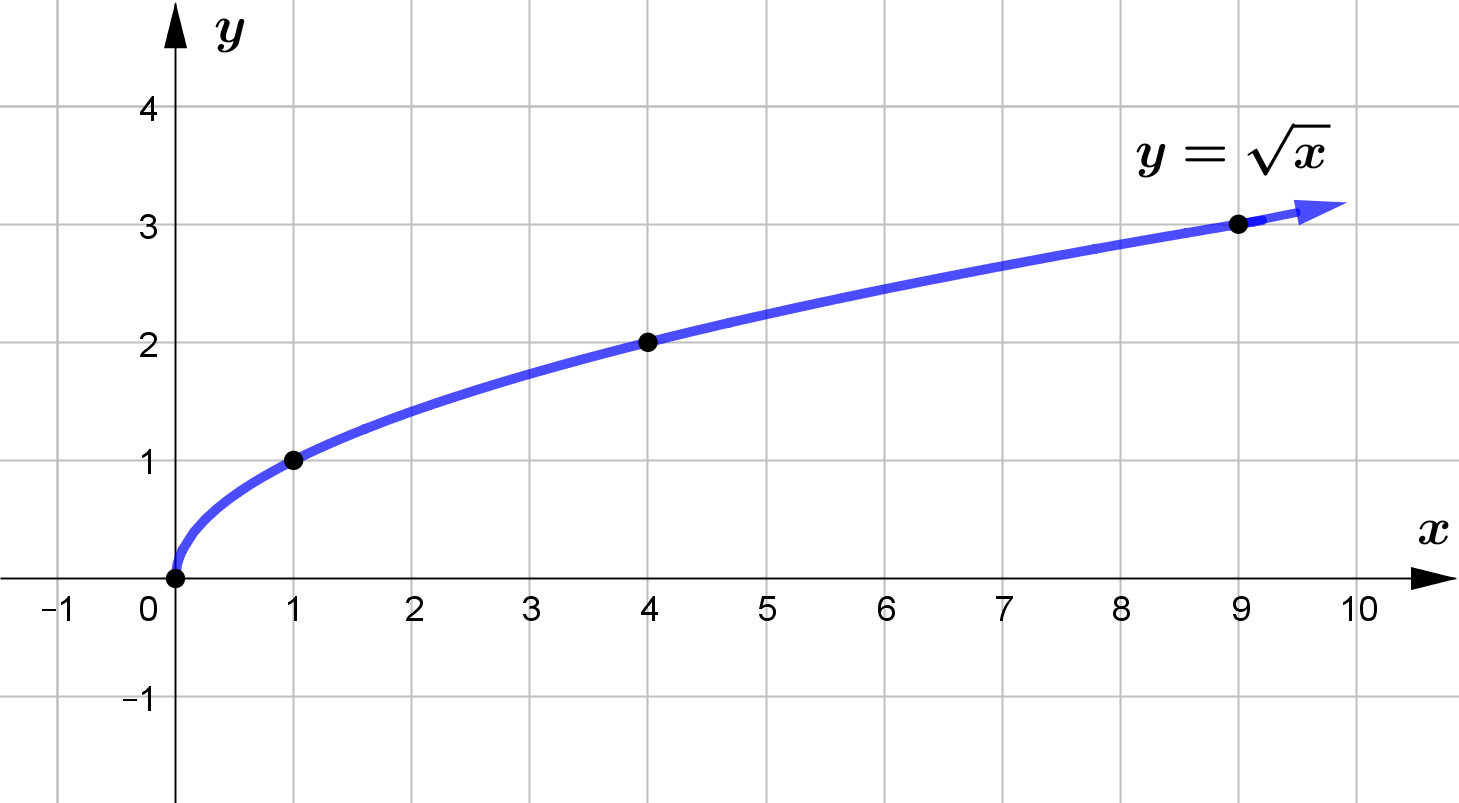
Given that $f(x)=\sqrt{x}$.
The following table represents the coordinate of some points on the graph $y=f(x)$.
$\begin{array}{|c|c|c|c|c|c|}
\hline x & 0 & 1 & 4 & 9 \\
\hline y & 0 & 1 & 2 & 3 \\
\hline
\end{array}$
| $ \text{(a)}$ | State the domain and range of $f(x)$. |
| $ \text{(b)}$ | Use table to sketch the graph of $y=f(x)$. |
| $ \text{(c)}$ | Describe the transformation that transforms the graph $y=\sqrt{x}$ to the graph $y=\sqrt{x-4}$. |
| $ \text{(d)}$ | The graph $y=\sqrt{x}$ is stretched by a scale factor of $2$ parallel to the $x$-axis and then it is translated $3$ units right. State the equation of the transformed graph. |
| $ \text{(e)}$ | The graph $y=\sqrt{x}$ is stretched by a scale factor of $5$ parallel to the $x$-axis. State the equation of the transformed graph. |
| $ \text{(f)}$ | If $(8,4)$ is a point on the graph $y=f(cx)$, what is the value of $c$? |