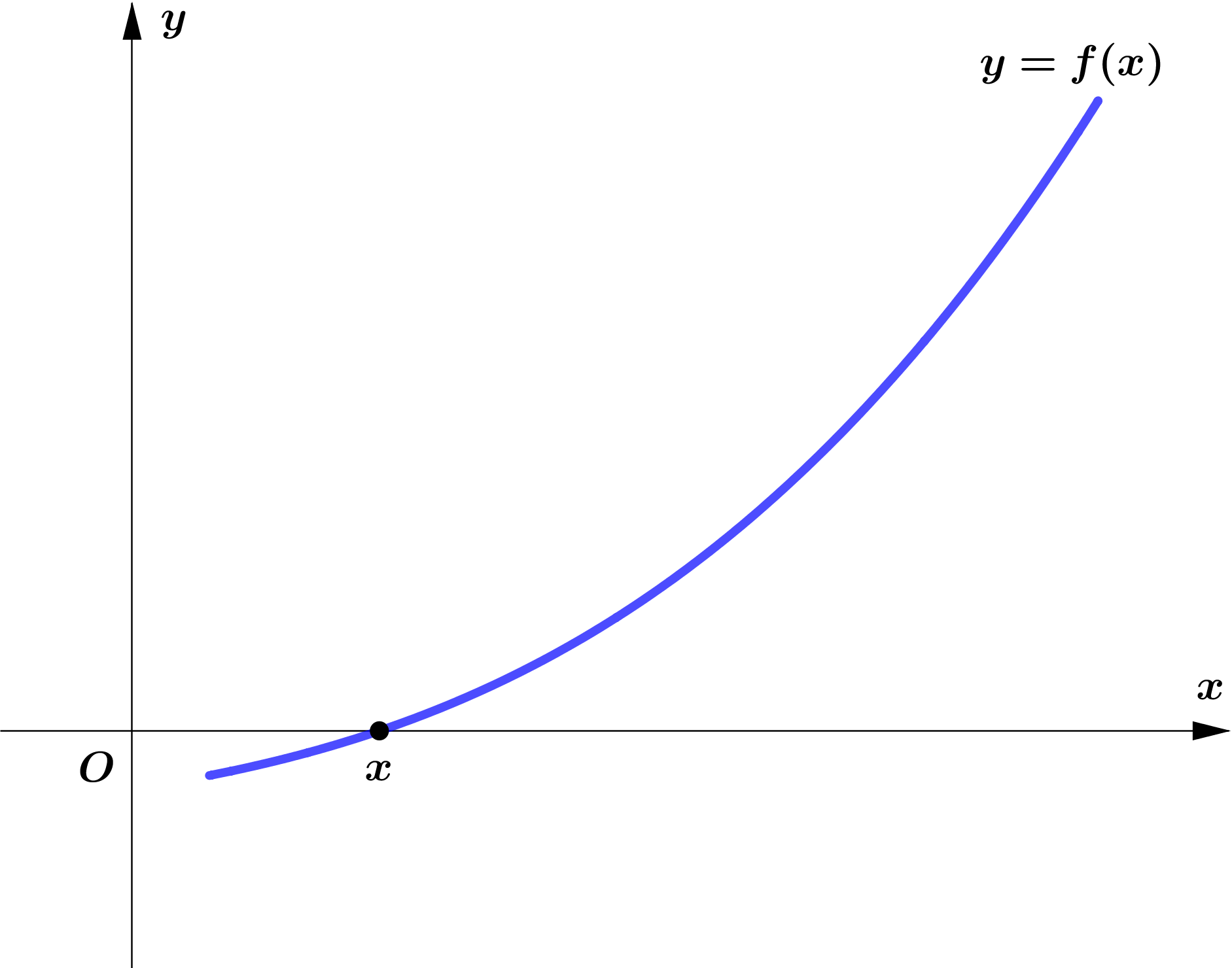
ပေးထားသော ပုံတွင် $x$ သည် $f(x)$ ၏ root ဖြစ်သည်ကို သိနိုင်ပါသည်။ $f(x)=0$ ၏ root ကို သင်္ချာ လုပ်ထုံးများ ဖြင့် အလွယ်တကူရှာ၍မရသည့် အခြေအနေဆိုပါစို့။ ထို့ကြောင့် ကြိုတင်ခန့်မှန်းထားသော $x_0$ ကို $f(x)$ root ဟု ယူဆမည်။ Figure 2 ကို ကြည့်ပါ။
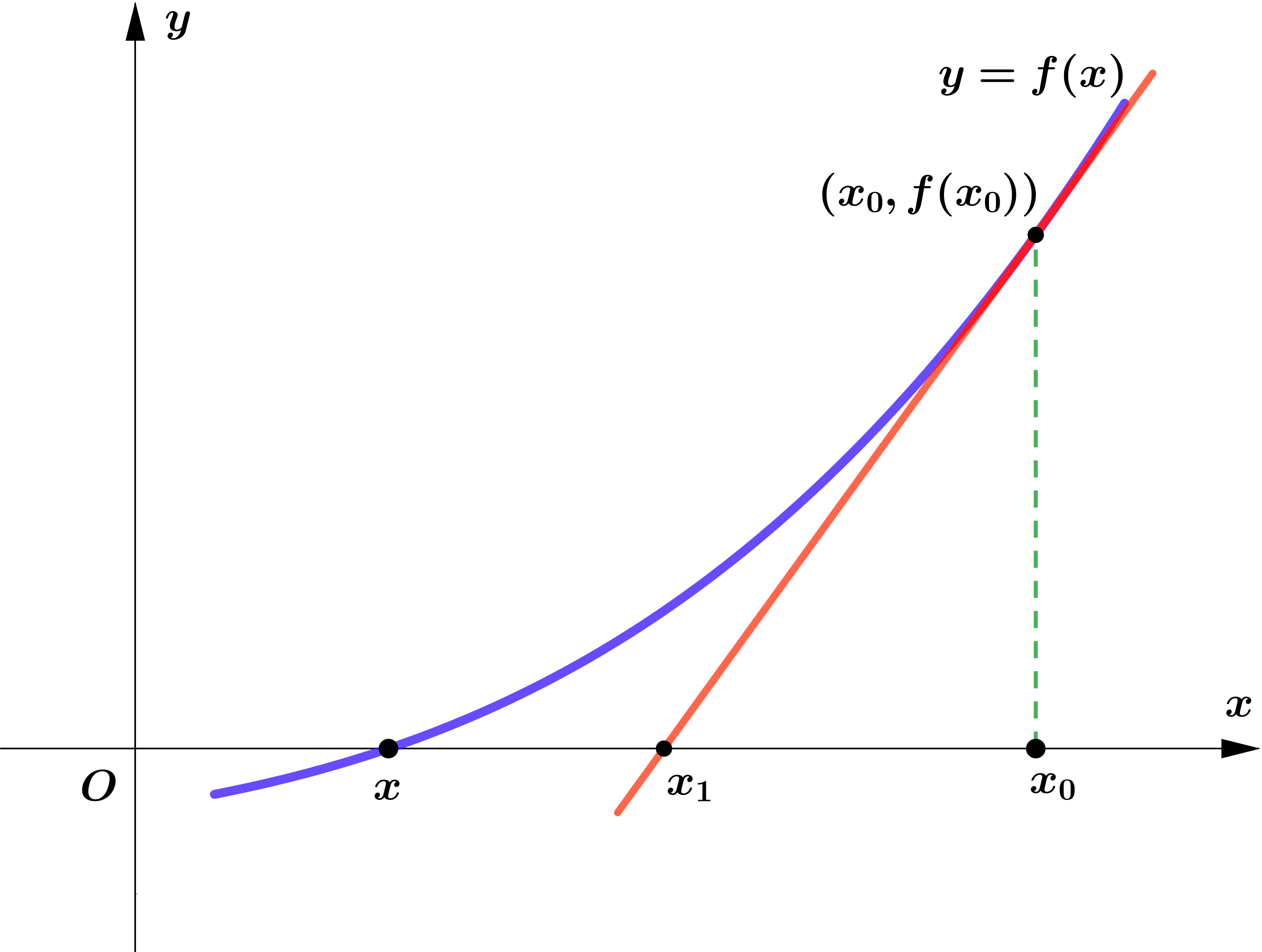
$f(x_0)\ne 0$ ဖြစ်သောကြာင့် $x_0$ သည် $f(x)$ ၏ root မဟုတ်ကြောင်းသိနိုင်သည်။ Graph ပေါ်ရှိ $(x_0,f(x_0))$ အမှတ်မှ tangent မျဉ်းတစ်ကြောင်းဆွဲလိုက်မည်။ အဆိုပါ tangent မျဉ်းသည် $x$ ဝင်ရိုးကို ဖြတ်သွားသောနေရာ $x_1$ သည် $f(x)=0$ ၏ root နှင့် နီးစပ်နေသည်ကို တွေ့ရမည်။ ထို့ကြောင့် $x_1$ ကို $f(x)=0$ ၏ approximate root ဟု ယူဆ၍ $x_1$ ကို ရှာပါမည်။
$x_1$ သည် tangent line က $x$-axis ကို ဖြတ်သောနေရာ ဖြစ်သောကြောင့် tangent line equation ကို ဦးစွာရှာမည်။ tangent line ၏ gradient မှာ $f'(x_0)$ ဖြစ်ပြီး $(x_0,f(x_0))$ အမှတ်သည် tangent line ပေါ်တွင်ရှိသည်။ ထို့ကြောင့် tangent line ၏ equation မှာ ...
$y=f'(x_0)(x-x_0)+f(x_0)$
ဖြစ်ပါမည်။ $x=x_1$ ဖြစ်လျှင် $y=0$ ဖြစ်မည်။ ထို့ကြောင့်
$$\begin{aligned} &0=f'(x_0)(x_1-x_0)+f(x_0)$\\\\ &f'(x_0)(x_1-x_0) = -f(x_0)\\\\ &x_1-x_0=-\frac{f(x_0)}{f'(x_0)}\\\\ \therefore\ & x_1=x_0-\frac{f(x_0)}{f'(x_0)}\\\\ \end{aligned}$$ဟူ၍ $x_1$ ကို ရှာနိုင်ပါသည်။
သို့ရာတွင် $x_1$ သည်လည်း $f(x)$ ၏ root မဟုတ်သေးပါ။ $f(x)$ ၏ root နှင့် နီးစပ်လာသည့် အခြေအနေတွင်သာ ရှိသေးသည်။ ထို့ကြောင့် အထက်တွင်ရှင်းလင်းခဲ့သော လုပ်ဆောင်ချက်အတိုင်း approximate root $(x_2)$ ကို ထပ်မံရှာယူပါမည်။ Figure 3 ကို ကြည့်ပါ။
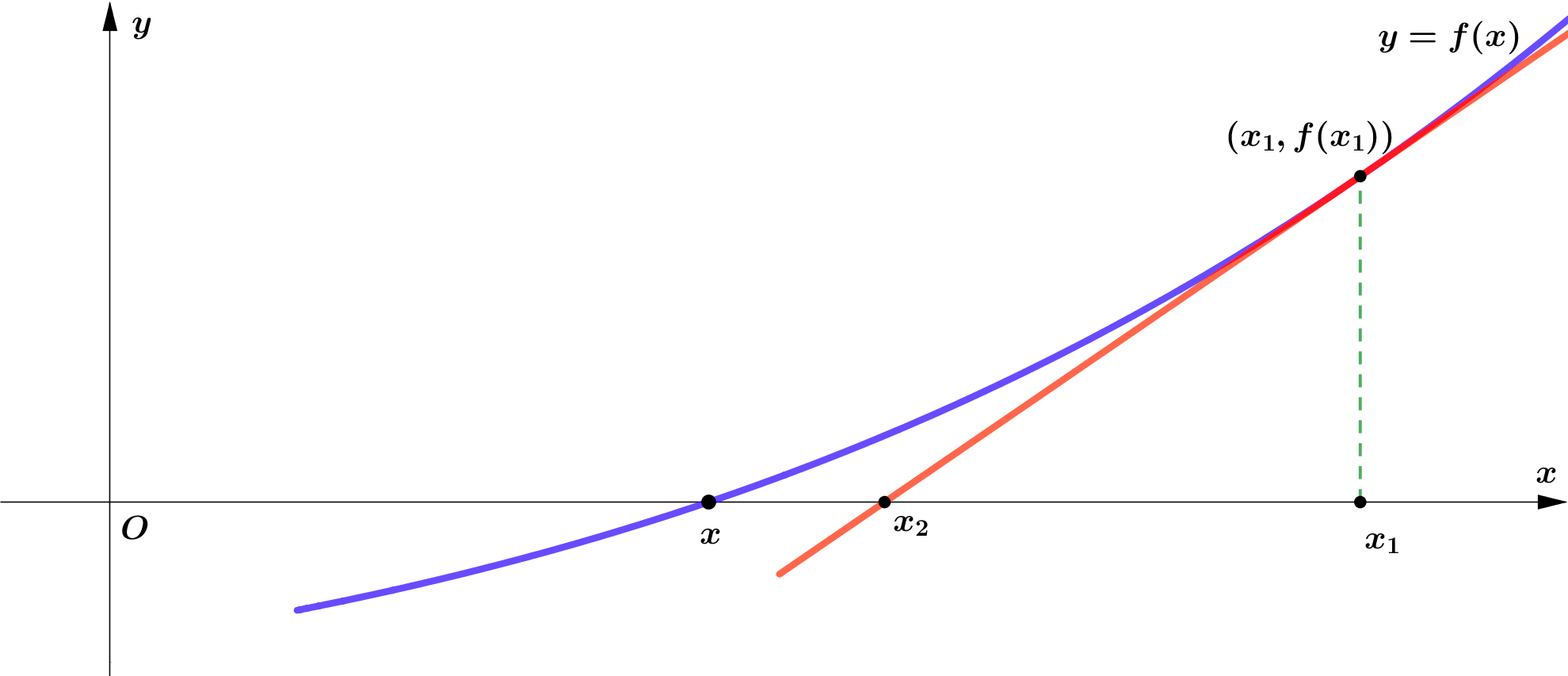
အထက်တွင် ဖော်ပြခဲ့သော လုပ်ဆောင်ချက်အတိုင်း $(x_1,f(x_1))$ အမှတ်ရှိ tangent line မှ $x$-axis ကို ဖြတ်သောအမှတ် $x_2$ ကို ဆက်လက်ရှာယူမည်။ ထိုအခါ $$x_2=x_1-\frac{f(x_1)}{f'(x_1)}$$ ဖြစ်မည်။ ၎င်းနည်းလမ်းအတိုင်း ထပ်ခါ ထပ်ခါ ရှာယူခြင်းဖြင့် $f(x)=0$ ၏ root နှင့် ထပ်တူကျလုနီးပါး ဖြစ်လာသော root တန်ဖိုးကို ရရှိပါမည်။ Figure 4 ကို ကြည့်ပါ။
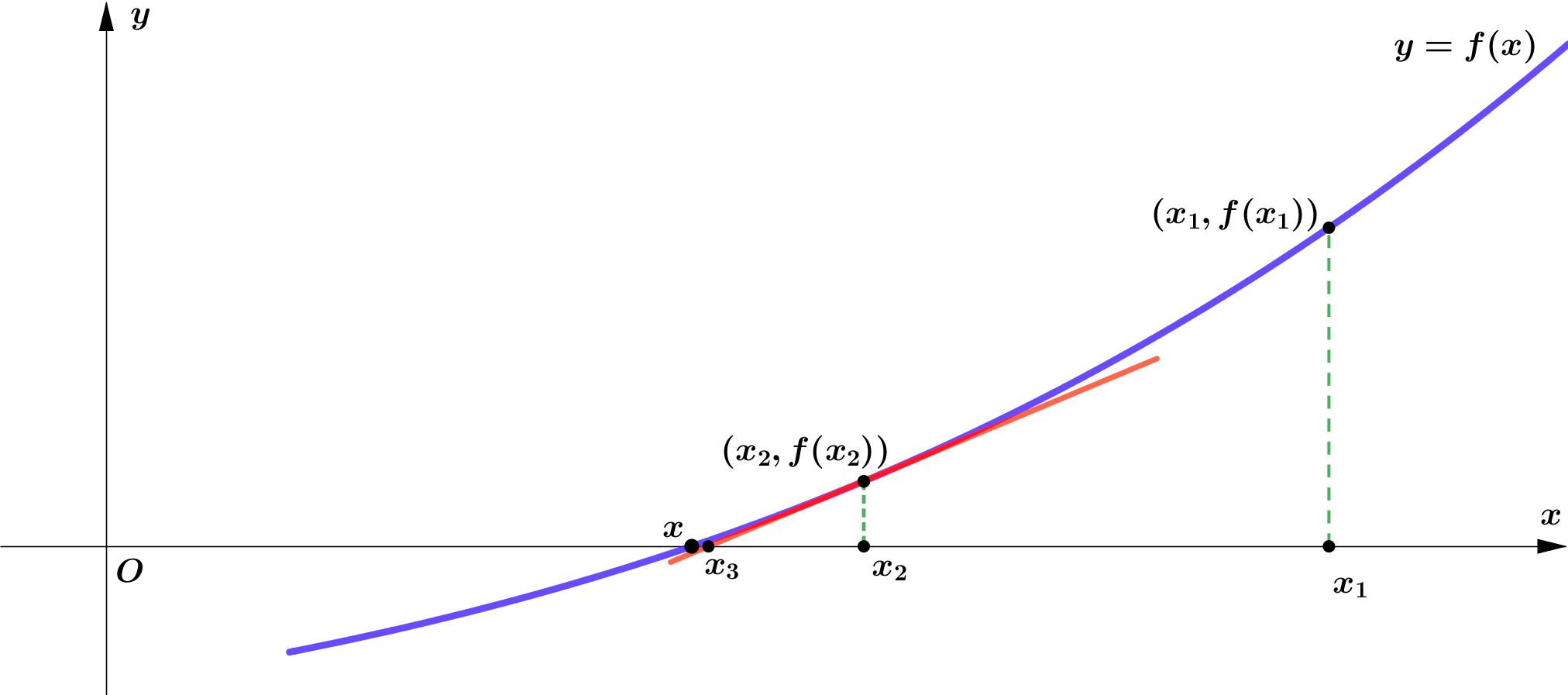
ဖော်ပြပါ ဆင့်ကဲရှာယူခြင်းနည်းလမ်းဖြင့် $f(x)=0$ ၏ root ကို ရှာယူနိုင်သော ပုံသေနည်း $x_{n+1}$ ကို အောက်ပါ အတိုင်းမှတ်သားနိုင်သည်။
$$\begin{array}{|c|} \hline x_{n+1}=x_n-\dfrac{f(x_n)}{f'(x_n)}\\ \hline \end{array}$$အထက်ဖော်ပြပါ ပုံသေနည်းဖြင့် root ရှာယူခြင်း process ကို Newton-Raphson Iteration Method ဟုခေါ်သည်။ လက်တွေ့ပုစ္ဆာဖြေရှင်းရာတွင် $x_{n+1}\approx x_n$ ဖြစ်သည့်အခါ Iteration Process ပြီးဆုံးပြီဟု မှတ်ယူနိုင်သည်။
အောက်ပါ အခြေနေတို့တွင် Newton-Raphson method ကို သုံး၍ မရနိုင်ပါ။
Case I
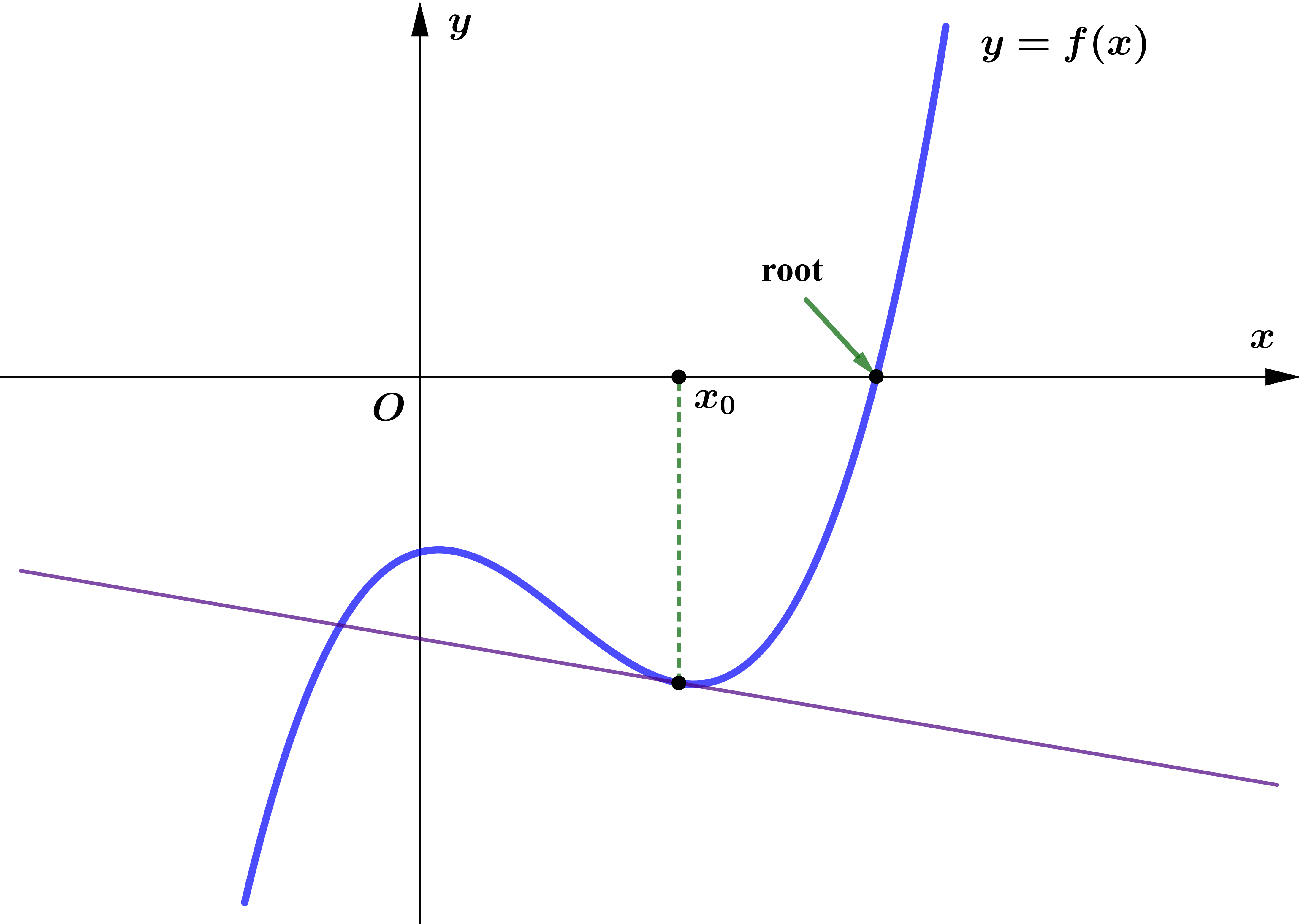
Starting point $x_0$ သည် အမှန်ဖြစ်သော root နှင့် ဝေးနေသောအခါ tangent သည် root နှင့် ပို၍ပို၍ ဝေးသော $x$ coordinate ကို ရောက်ရှိသွားပြီး Newton-Raphson Formula သည် divergent ဖြစ်သွားမည်။
Case II
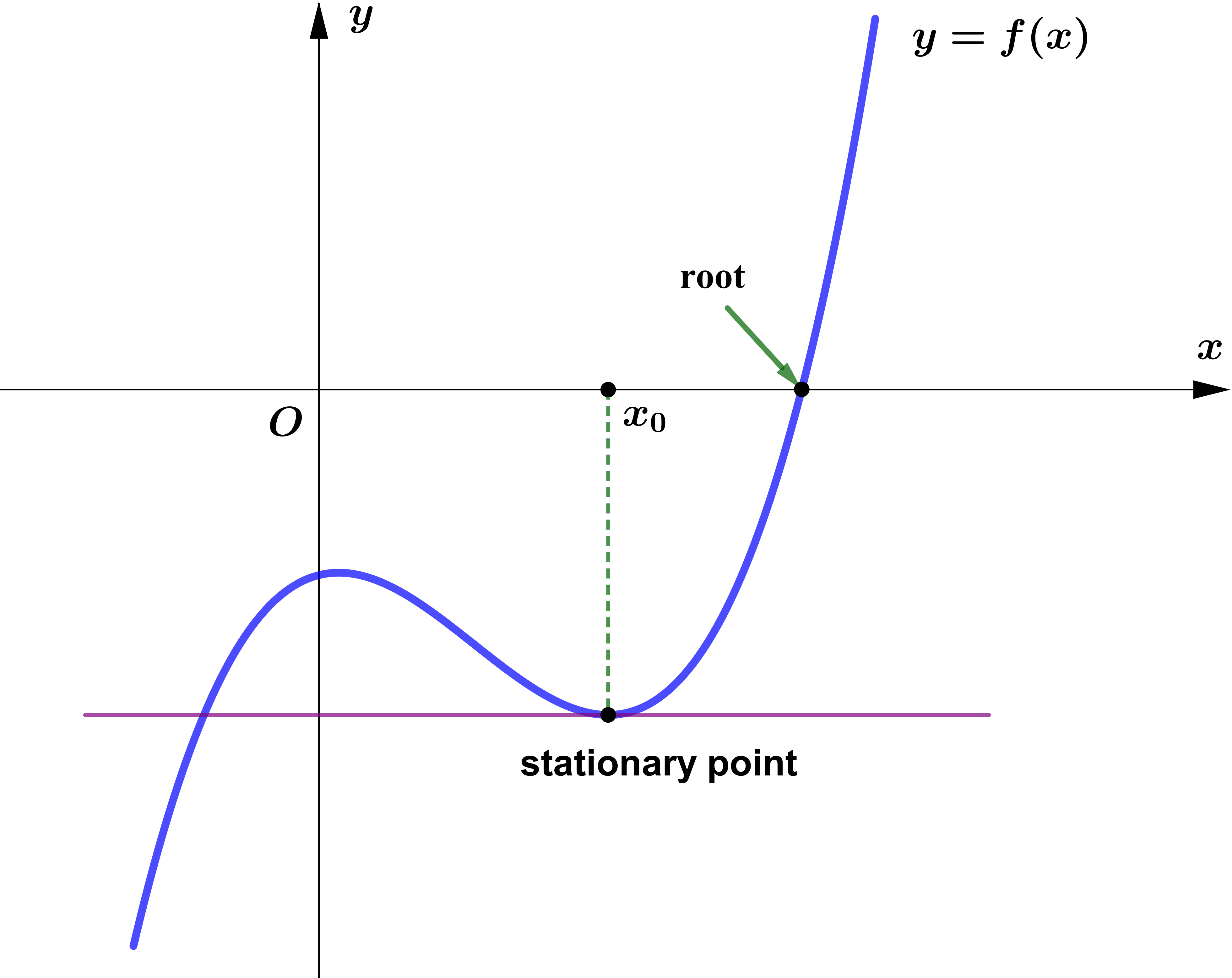
$f'(x_0)=0$ ဖြစ်လျှင် tangent သည် horizontal ဖြစ်သွားမည်။ $(x_0, f(x_0))$ stationary point ဖြစ်နေမည်။ ထိုအခါ tangent သည် $x$-axis ကို ဘယ်တော့မျှ မဖြတ်တော့ပါ။ ထိုအခြေအနေတွင် $ x_{n+1}=x_n-\dfrac{f(x_n)}{f'(x_n)}$ သည် undefined ဖြစ်သွား၍ Newton-Raphson Formula ကို သုံး၍မရနိုင်ပါ။
Example (1)
Using Newton-Raphson method, find the approximate value of $\sqrt[3]{19}$ in four decimal places.
|
Let $ \sqrt[3]{19}=x$. $\begin{aligned} &\\ \therefore \ & x^3 = 19\\\\ &x^3 - 19=0\\\\ \end{aligned}$ Hence, $ \sqrt[3]{19}$ is the root of the equation $x^3 - 19=0$. $\begin{aligned} &\\ &\text{Let } f(x)=x^3-19\\\\ \therefore \ & f'(x) = 3x^2\\\\ &x_{n+1}=x_n-\frac{{x_n}^3-19}{3{x_n}^2}\\\\ \end{aligned}$ Since $2^3=8$ and $3^3=27$, $ \sqrt[3]{19}$ is between $2$ and $3$. Let $x_0=3$. $\begin{array}{|l|l|c|} \hline \quad x_n & x_{n+1} & \text{Remark}\\ \hline 3 & 2.703704 & x_{n+1}\ne x_n \\ \hline 2.703704 & 2.668861 & x_{n+1}\ne x_n \\ \hline 2.668861 & 2.668402 & x_{n+1}\ne x_n \\ \hline 2.668402 & 2.668402 & x_{n+1}\approx x_n \\ \hline \end{array}$ $\therefore\ \sqrt[3]{19}=2.6684$ |
|---|
Example (2)
Show that equation $e^x=3x+1$ has a root $\alpha=0$. Show by calculation that this equation also has a root, $\beta$, such that $1 < \beta < 2 $. Hence using Newton-Raphson method, find the $\beta$ correct to 4 decimal places.
|
$\begin{aligned}
&e^x=3x+1\\\\
\therefore\ & e^x-3x-1=0\\\\
&\text{Let } f(x)=e^x-3x-1\\\\
&f(0)=e^0-3(0))-1\\\\
&f(0)=1-0)-1=0\\\\
\therefore\ & x=0 \text{ is a root of } f(x).\\\\
&f(1)=e^1-3-1=-1.28172 < 0\\\\
&f(2)=e^2-3(2)-1=0.389056 >0\\\\
\therefore\ & 1 < \beta < 2\\\\
&f'(x)=e^x-3\\\\
\therefore\ & x_{n+1}=x_n-\frac{e^{x_n}-3{x_n}-1}{e^{x_n}-3}\\\\
\end{aligned}$ Let $x_0=2$. $\begin{array}{|l|l|c|} \hline \quad x_n & x_{n+1} & \text{Remark}\\ \hline 2 & 1.911358 & x_{n+1}\ne x_n \\ \hline 1.911358 & 1.911358 & x_{n+1}\approx x_n \\ \hline \end{array}$ $\therefore\ \beta=1.9114$ |
|---|
Example (3)
Given that $f(x)=x^3 - x - 1$. Show that $f(x)=0$ has a root between $1$ and $2$. Taking $x_0=1.5$, use Newton-Raphson method to find the root of $f(x)=0$ correct to $3$ decimal places.
|
$\begin{aligned}
&f(x)=x^3 - x - 1\\\\
&f(1)=1-1-1=-1< 0\\\\
&f(2)=8-2-1=5 > 0\\\\
\therefore\ & f(x)=0 \text{ has a root between } 1 \text{ and } 2. \\\\
&f'(x)=3x^2-1\\\\
\therefore\ & x_{n+1}=x_n-\frac{{x_n}^3 - {x_n} - 1}{3{x_n}^2-1}\\\\
\end{aligned}$ Taking $x_0=1.5$, $\begin{array}{|l|l|c|} \hline \quad x_n & x_{n+1} & \text{Remark}\\ \hline 1.5 & 1.34783 & x_{n+1}\ne x_n \\ \hline 1.34783 & 1.32520 & x_{n+1}\ne x_n \\ \hline 1.32520 & 1.32472 & x_{n+1}\approx x_n \\ \hline 1.32472 & 1.32472 & x_{n+1}\approx x_n \\ \hline \end{array}$ $\therefore\ $ The required root is $x=1.325$. |
|---|

