2021 (May-June) CIE (9709-Pure Mathematics 1), Paper 1/21 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
-
Solve the inequality $|3x − 7| < |4x + 5|$. [4]
-
By first expanding $\sin(\theta + 30^{\circ})$, solve the equation $\sin(\theta + 30^{\circ})\operatorname{cosec}\theta = 2$ for $0^{\circ} < \theta < 360^{\circ}$. [6]
-
(a) Show that $(\sec x+\cos x)^{2}$ can be expressed as $\sec ^{2} x+a+b \cos 2 x$, where $a$ and $b$ are constants to be determined. [2]
(b) Hence find the exact value of $\displaystyle\int_{0}^{\frac{1}{4} \pi}(\sec x+\cos x)^{2} dx$. [4] -
A curve has parametric equations $$x=\ln (2 t+6)-\ln t, \quad y=t \ln t .$$
(a) Find the value of $t$ at the point $P$ on the curve for which $x=\ln 4$. [3]
(b) Find the exact gradient of the curve at $P$. [5] -
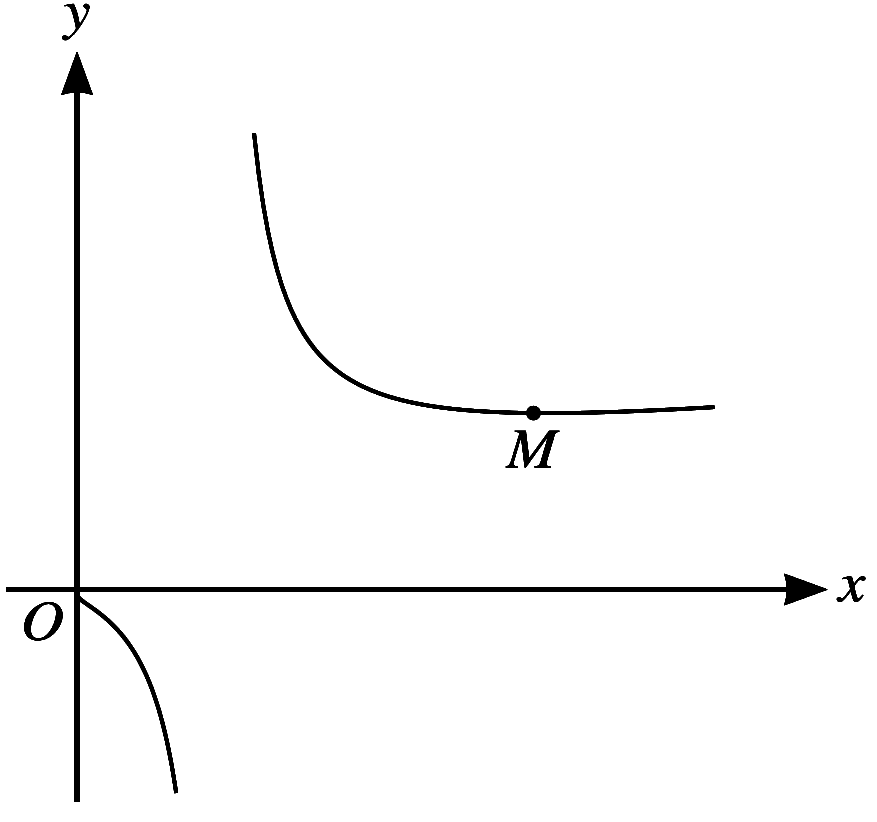
The diagram shows the curve with equation $y=\dfrac{3 x+2}{\ln x}$. The curve has a minimum point $M$.
(a) Find an expression for $\dfrac{dy}{dx}$ and show that the $x$-coordinate of $M$ satisfies the equation $x=\dfrac{3 x+2}{3 \ln x}$. [3]
(b) Use the equation in part (a) to show by calculation that the $x$-coordinate of $M$ lies between $3$ and $4$. [2]
(c) Use an iterative formula, based on the equation in part (a), to find the $x$-coordinate of $M$ correct to $5$ significant figures. Give the result of each iteration to $7$ significant figures. [3] -
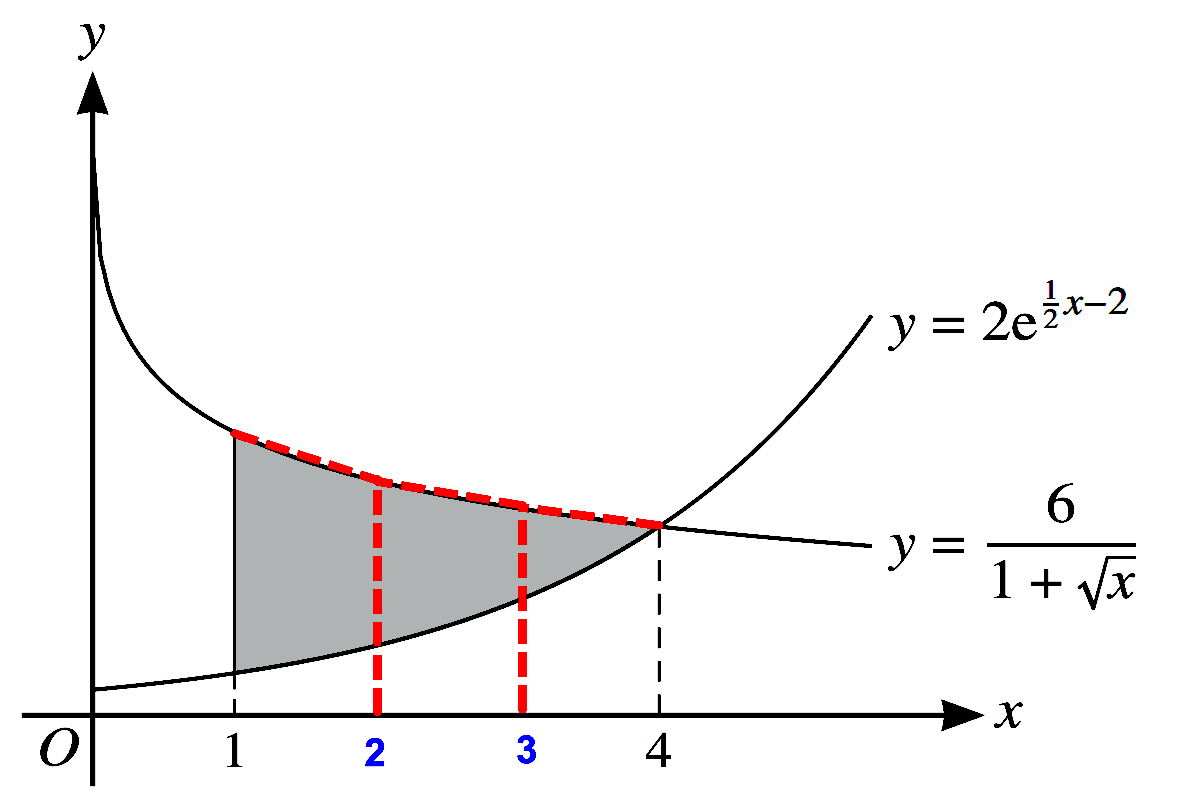
(a) Use the trapezium rule with three intervals to find an approximation to $\displaystyle\int_{1}^{4} \frac{6}{1+\sqrt{x}}dx$. Give your answer correct to $5$ significant figures. [3]
(b) Find the exact value of $\displaystyle\int_{1}^{4} 2 e^{\frac{1}{2} x-2}dx$. [3]
(c) The diagram shows the curves $y=\dfrac{6}{1+\sqrt{x}}$ and $y=2 e^{\frac{1}{2} x-2}$ which meet at a point with $x$-coordinate $4$ . The shaded region is bounded by the two curves and the line $x=1$.
Use your answers to parts (a) and (b) to find an approximation to the area of the shaded region. Give your answer correct to $3$ significant figures. [2]
(d) State, with a reason, whether your answer to part (c) is an over-estimate or under-estimate of the exact area of the shaded region. [1] -
The polynomial $\mathrm{p}(x)$ is defined by $p(x)=a x^{3}-11 x^{2}-19 x-a,$ where $a$ is a constant. It is given that $(x-3)$ is a factor of $p(x)$.
(a) Find the value of $a$. [2]
(b) When $a$ has this value, factorise $p(x)$ completely. [3]
(c) Hence find the exact values of $y$ that satisfy the equation $p\left(e^{y}+e^{-y}\right)=0$. [4]