Graph of $y=|f(x)|$

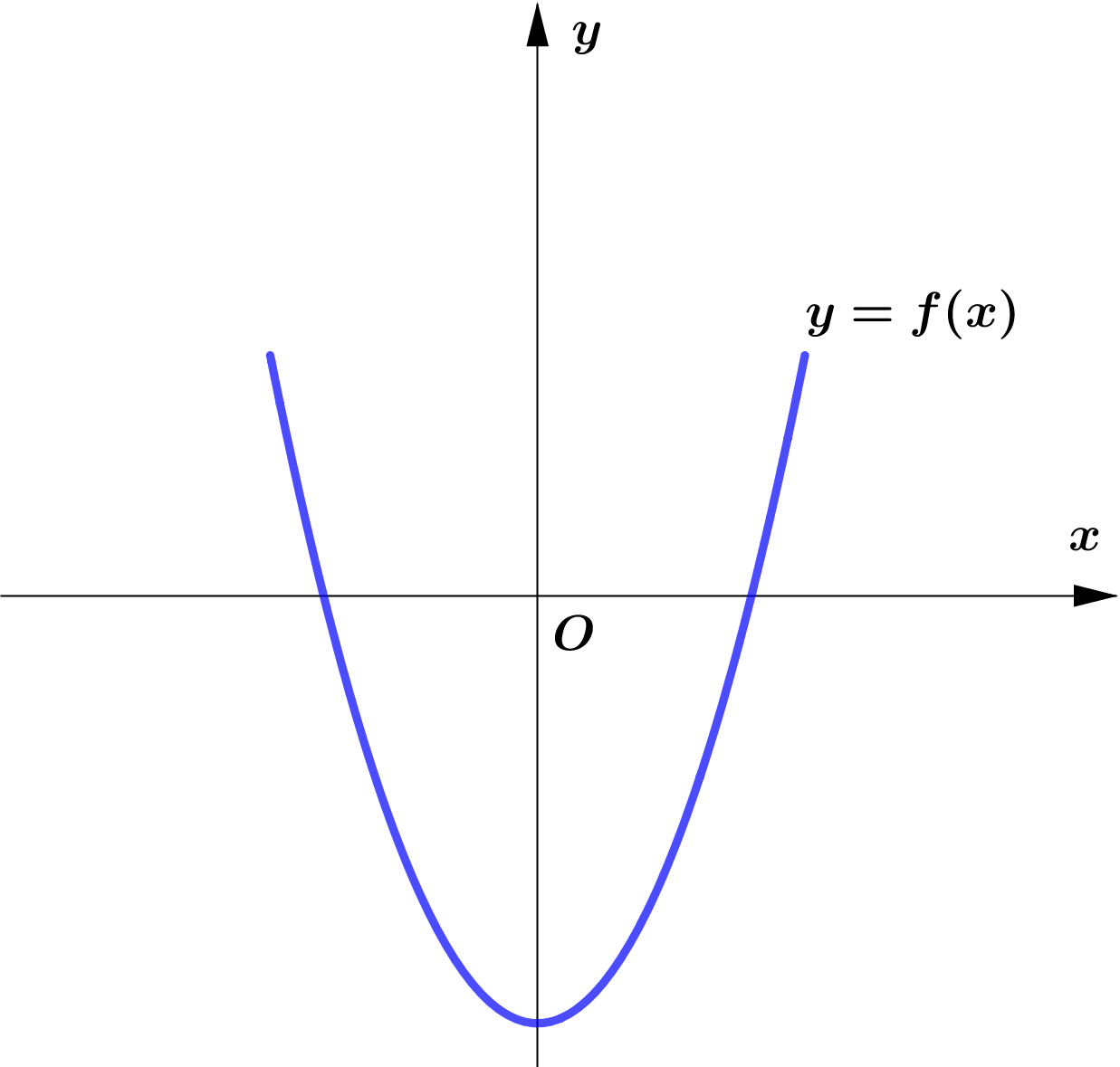
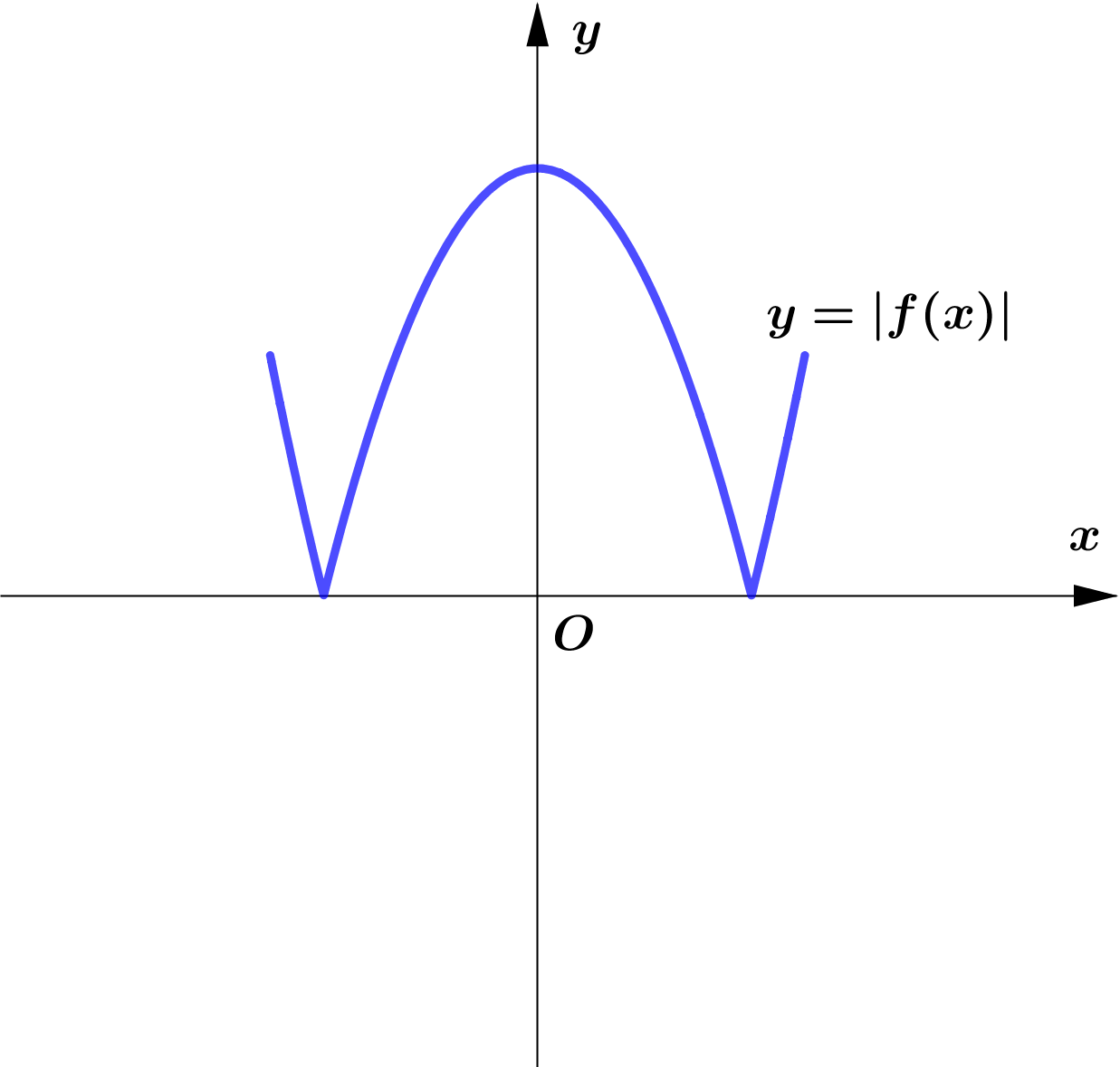
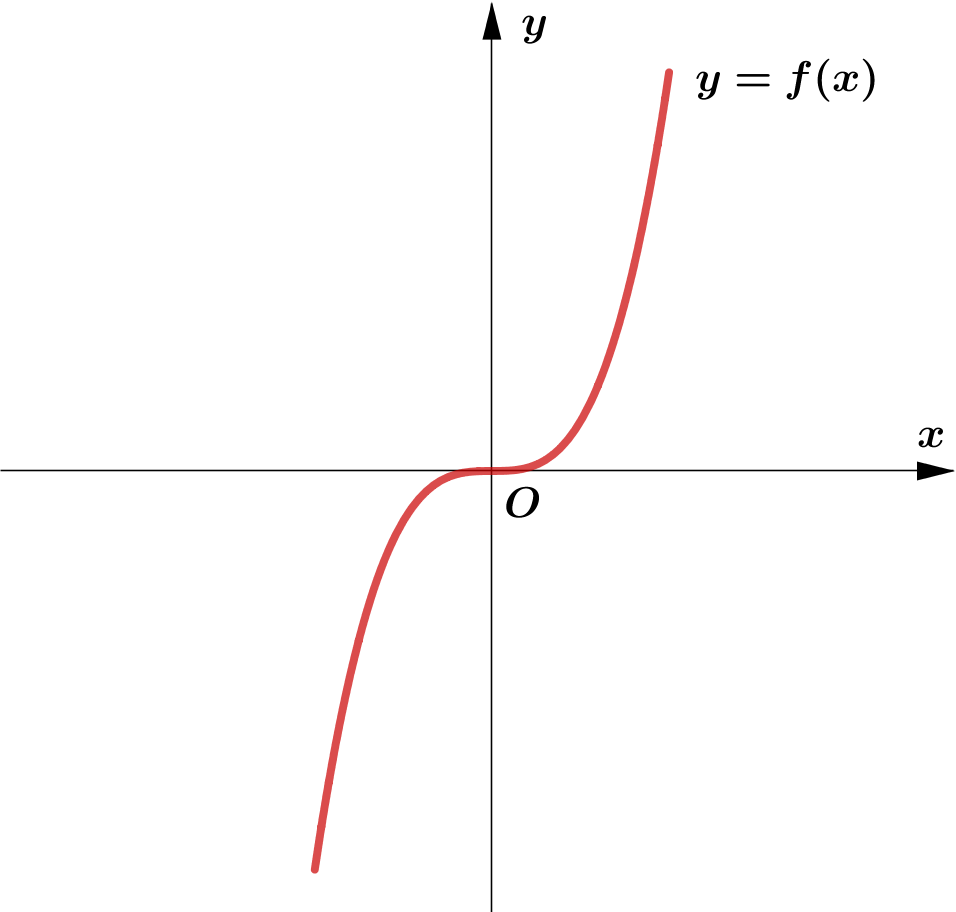
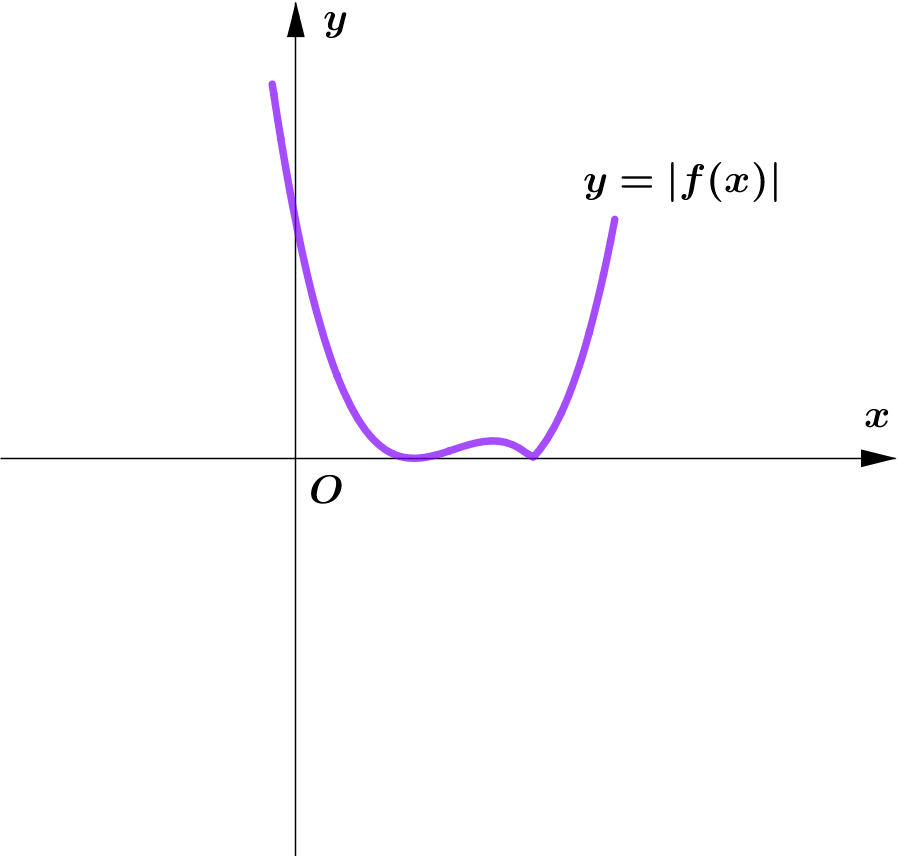
Graphs of $y=|f(x)|$

Modulus Function တစ်ခု၏ image (output) များသည် $0$ သို့မဟုတ် $0$ ထက်အမြဲကြီးကြောင်း သိရှိခဲ့ပြီး ဖြစ်သည်။ ထို့ကြောင့် Function တစ်ခု၏ modulus grph ကို sketch လုပ်သည့်အခါ မူလ (parent) Function ၏ $x$-axis အောက်ရှိ graph ၏ အစိပ်အပိုင်းများကို $x$-axis နှင့် ခေါက်ချိုးညီ $x$-axis အပေါ်သို့ ရွှေ့ပေးလိုက်ခြင်း (reflection about $x$-axis) ဖြစ်သည်။

Graph တစ်ခုလုံးကို reflect လုပ်ခြင်းမဟုတ်ပဲ Negative Portion ကိုသာ ရွှေ့ပေးခြင်း ဖြစ်သည်ကို သတိပြုရပါမည်။ အောက်ပါ ဥပမာများကို ‌ လေ့လာကြည့်ပါ။

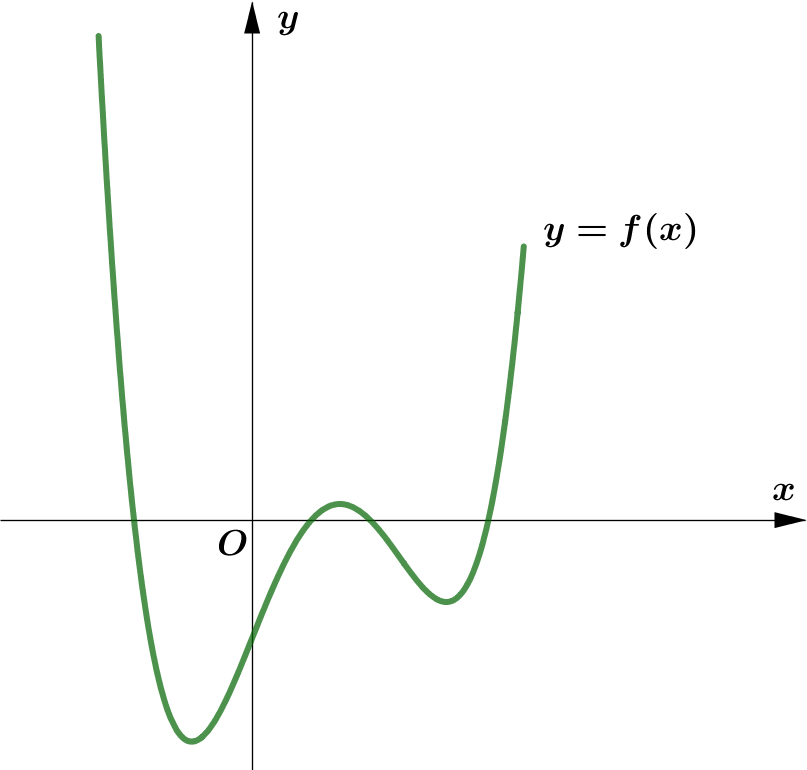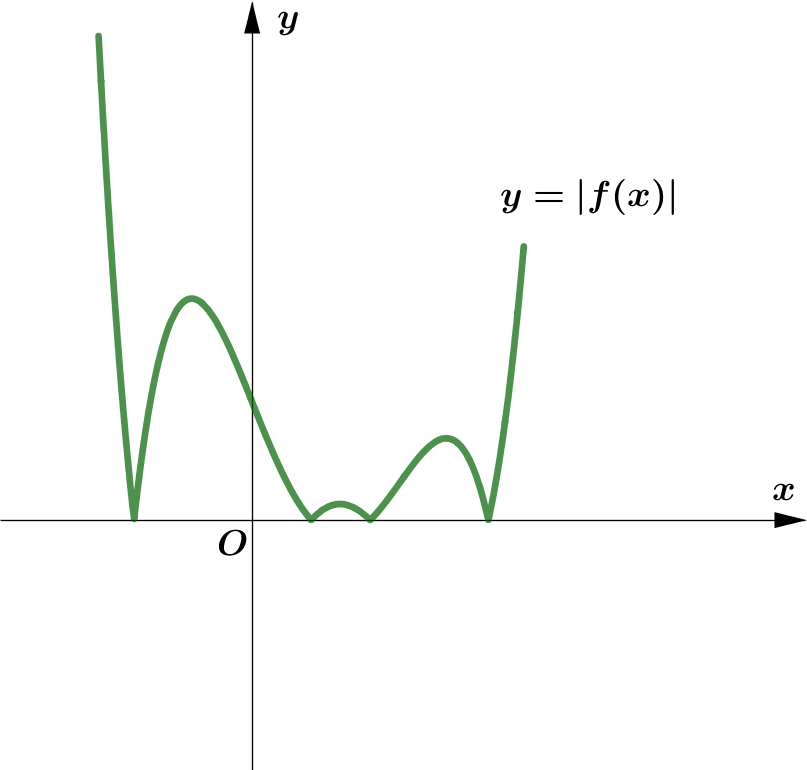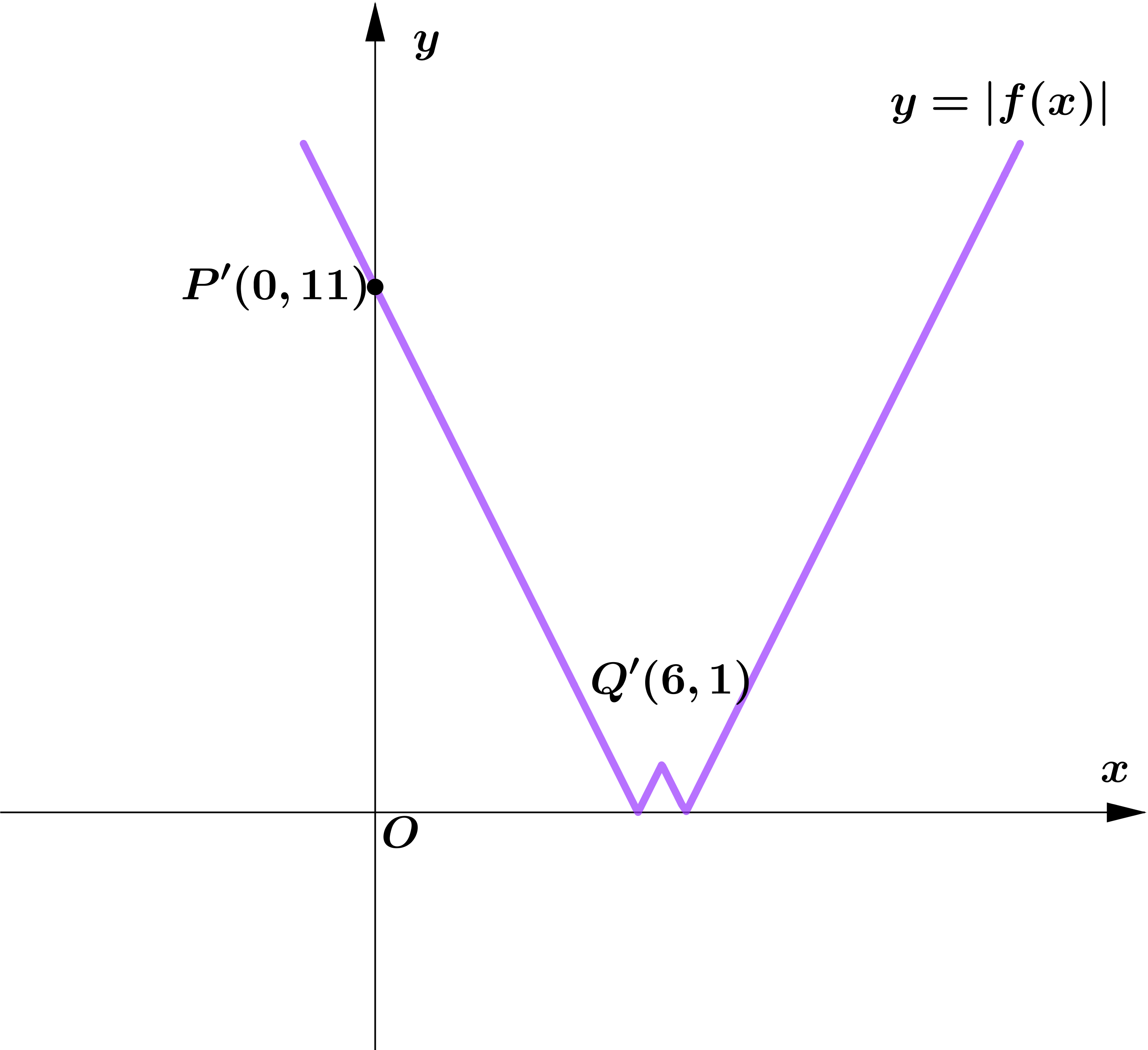
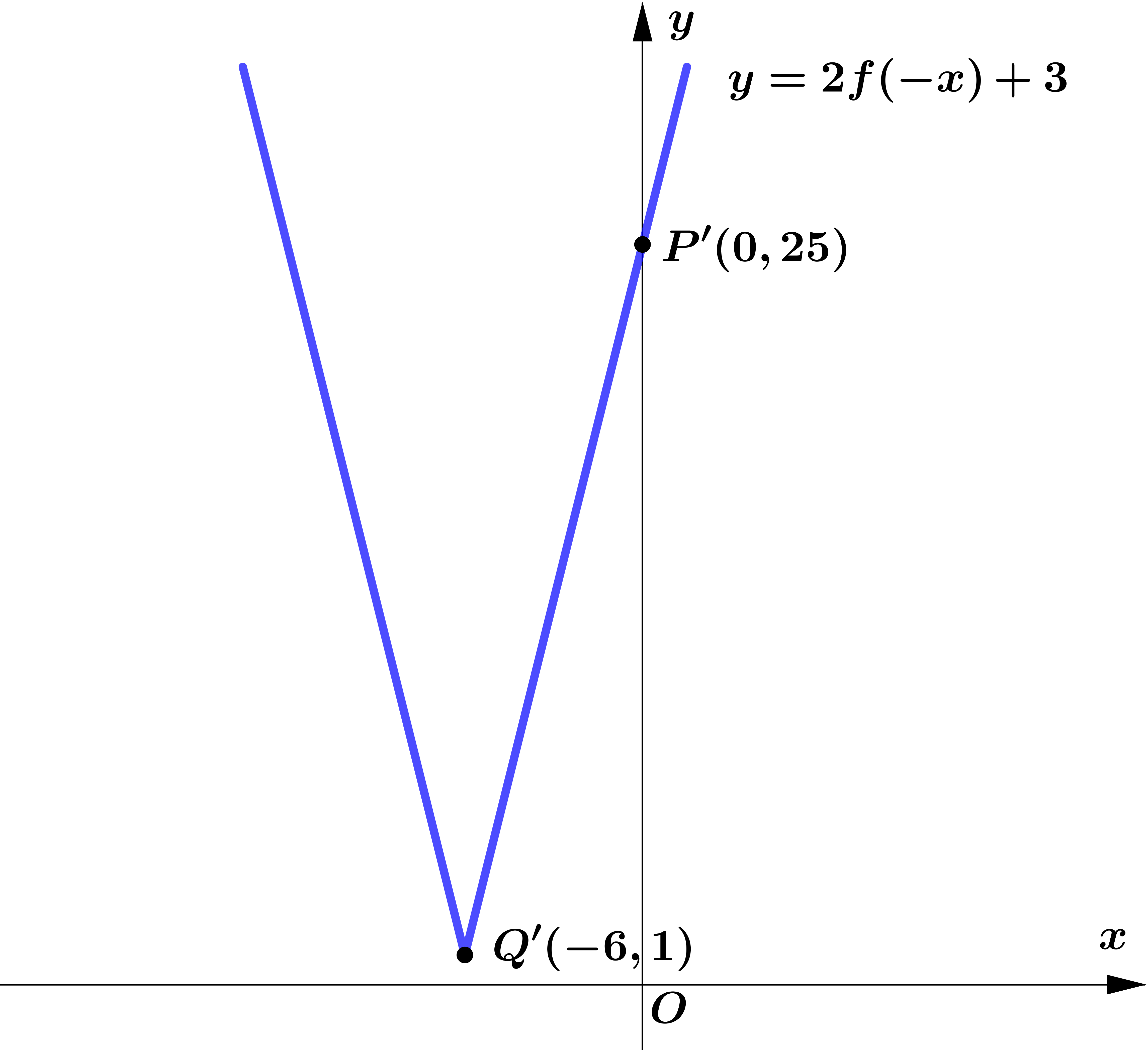
Question 1

Figure 1

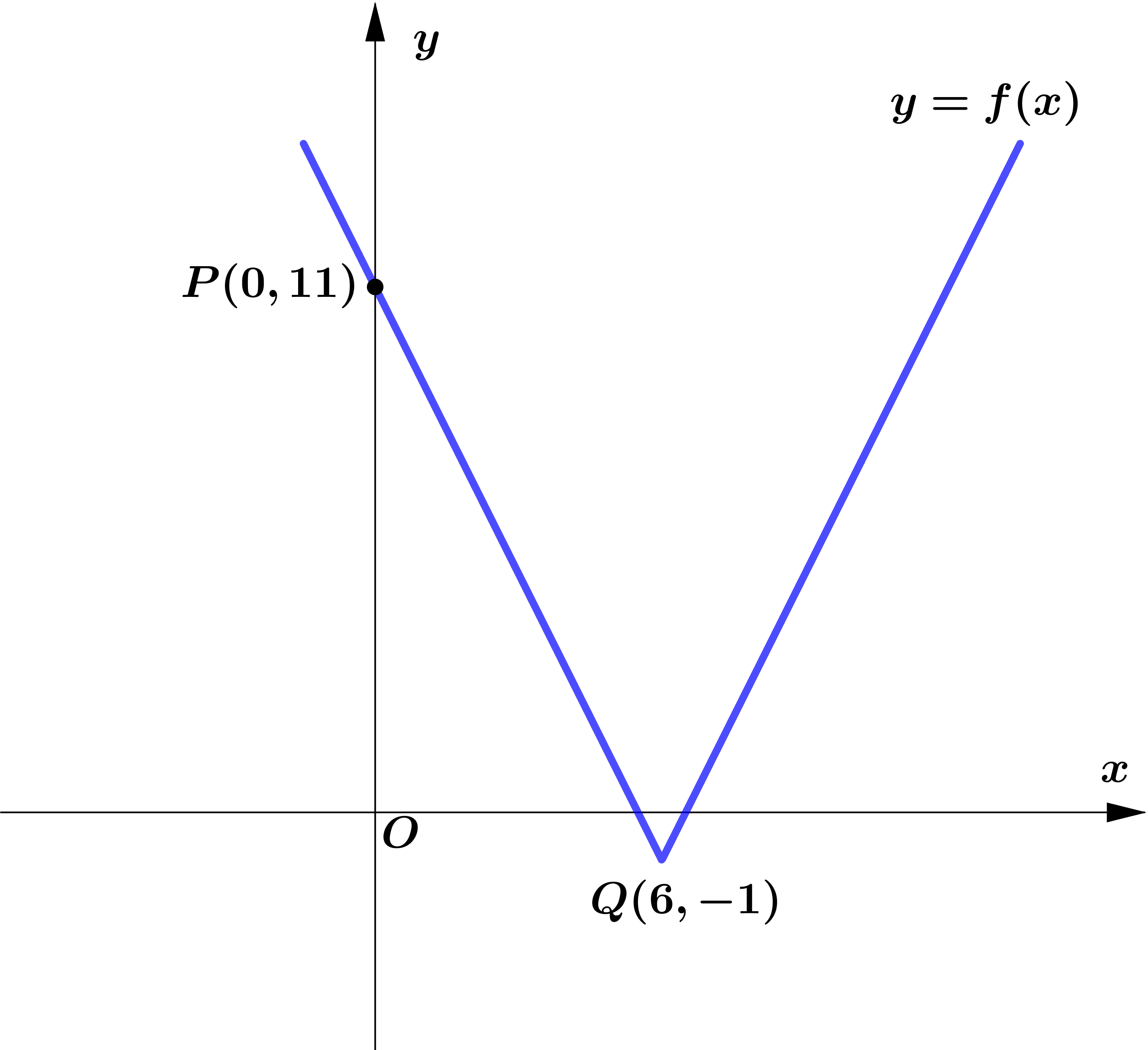
Figure 1 shows part of the graph with equation $y=f(x), x \in \mathbb{R}$.

The graph consists of two line segments that meet at the point $Q(6,-1)$.

The graph crosses the $y$-axis at the point $P(0,11)$.

Sketch, on separate diagrams, the graphs of

(a) $y=|f(x)|$

(b) $y=2 f(-x)+3$

On each diagram, show the coordinates of the points corresponding to $P$ and $Q$.

Given that $f(x)=a|x-b|-1$, where $a$ and $b$ are constants,

(c) state the value of $a$ and the value of $b$.

(a) On the graph $y=|f(x)|$. The point $P$ is unchanged. The mapped point of $Q$ is $(6, 1)$. (b) On the graph $y=2f(-x)+3$. $P(0,11)\rightarrow P'\left(0, 2(11)+3\right)=P'\left(0, 25\right)$ $Q(6,-1)\rightarrow Q'\left(-6, 2(-1)+3\right)=Q'\left(-6, 1\right)$ (c) $\ f(x)=a|x-b|-1$ $\begin{aligned} &\\ \therefore\quad & (b, -1)= (6, -1)\\\\ & b=6\\\\ \therefore\quad & a|0-6|-1 = 11\\\\ & a=2 \end{aligned}$

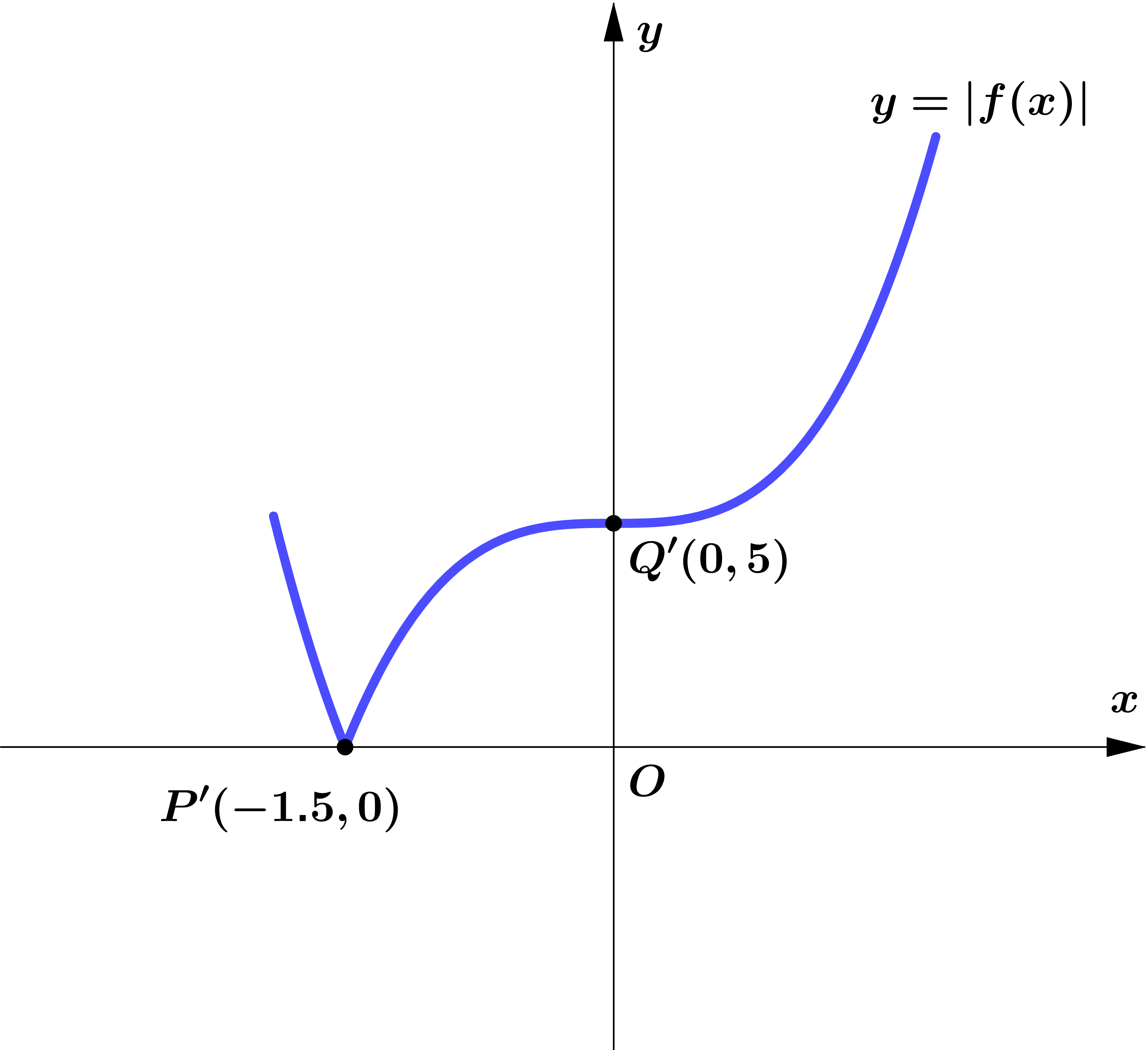
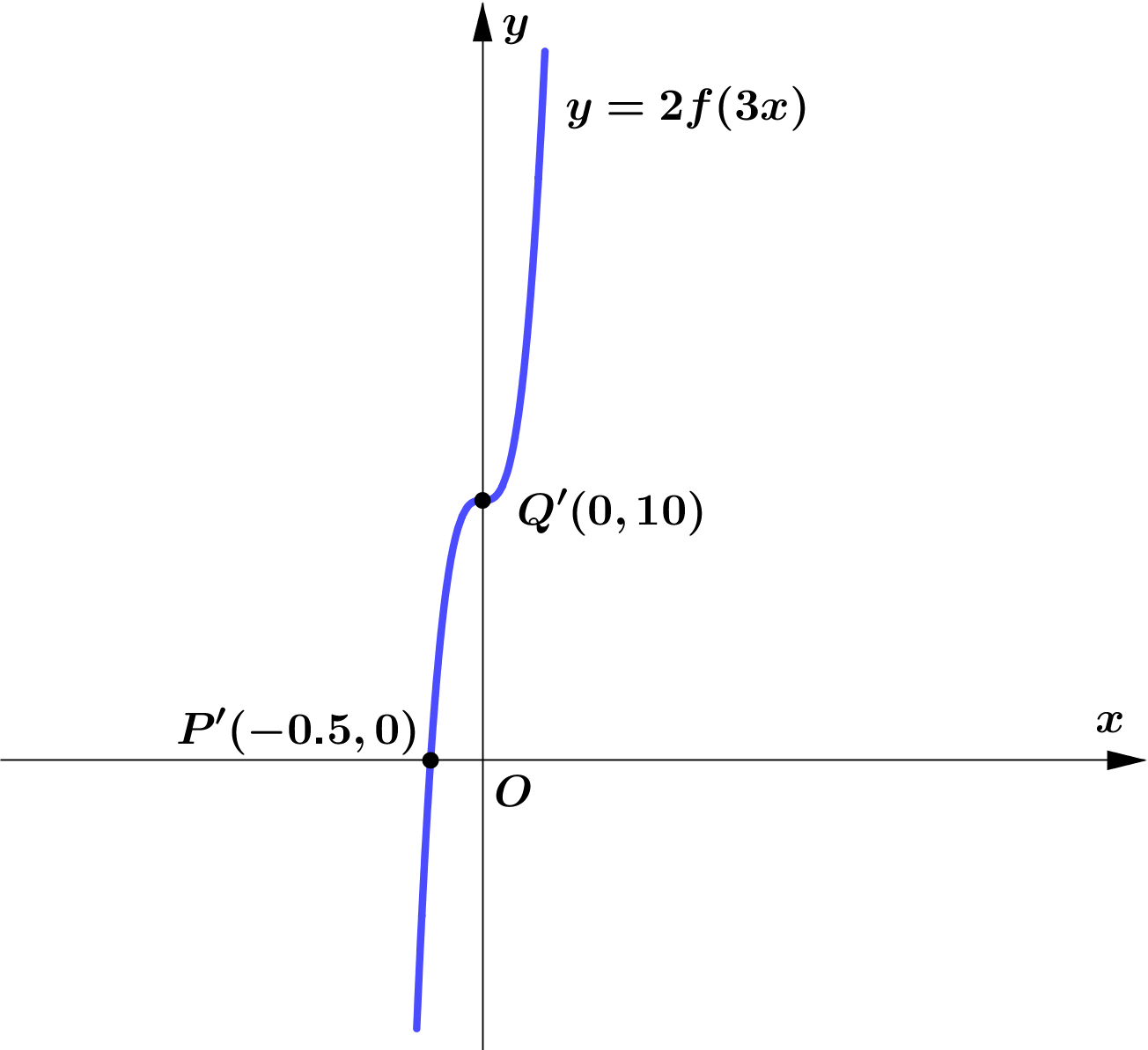
Question 2

Figure 2

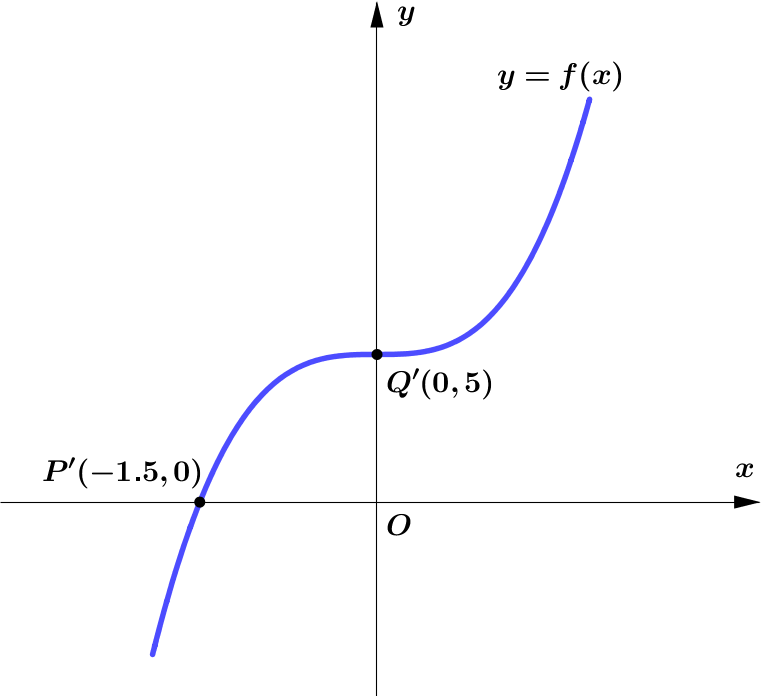
Figure 2 shows part of the curve with equation $y=f(x)$.

The curve passes through the points $P(-1.5,0)$ and $Q(0,5)$ as shown.

On separate diagrams, sketch the curve with equation

(a) $y=|f(x)|$

(b) $y=2f(3 x)$

Indicate clearly on each sketch the coordinates of the points at which the curve crosses or meets the axes.

(a) On the graph $y=|f(x)|$. The coordinates of both points $P$ and $Q$ are unchanged. (b) On the graph $y=2f(3x)$. $P(-1.5,0)\rightarrow P'\left(\dfrac{-1.5}{3}, 2(0)\right)=P'\left(-0.5, 0\right)$ $Q(0,5)\rightarrow Q'\left(0, 2(5)\right)=Q'\left(0, 10\right)$

Question 3

Figure 3

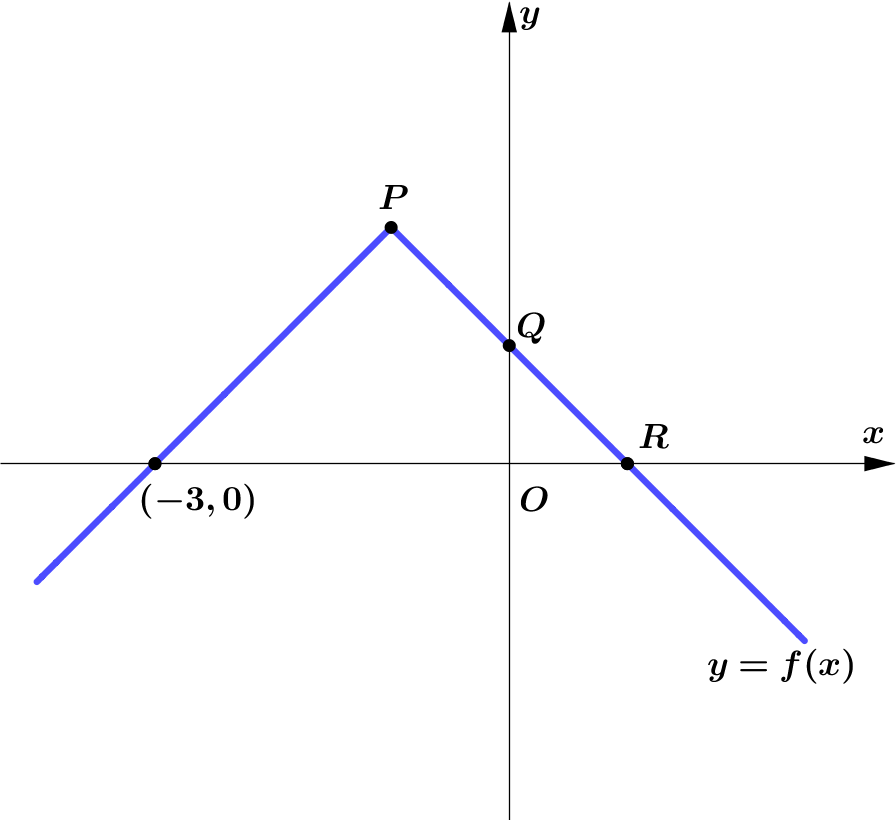
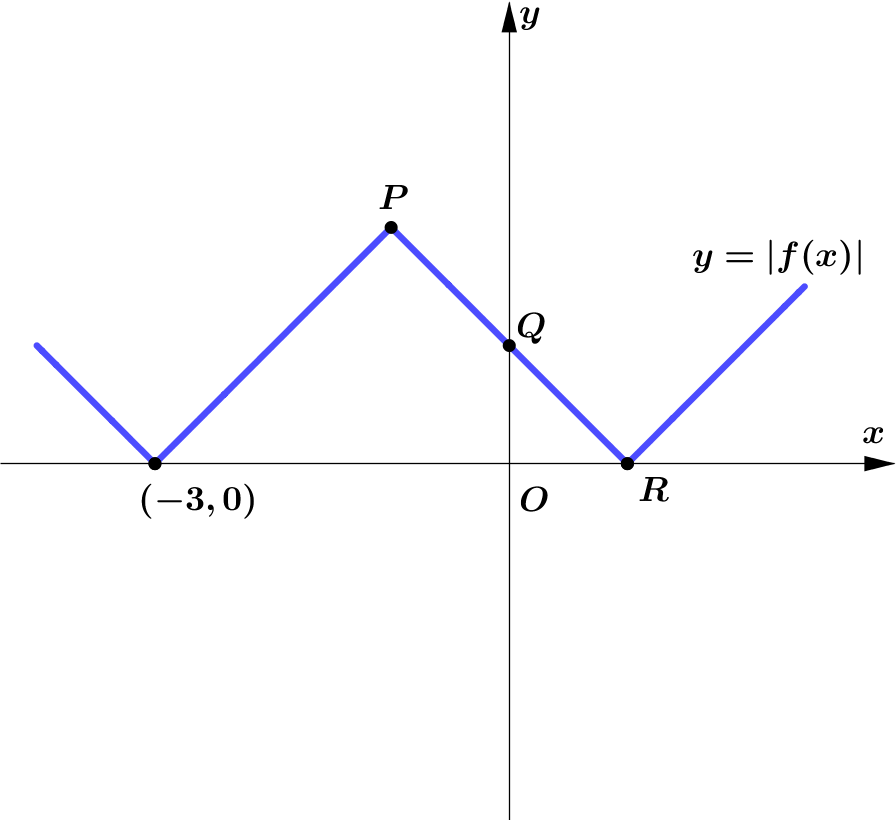
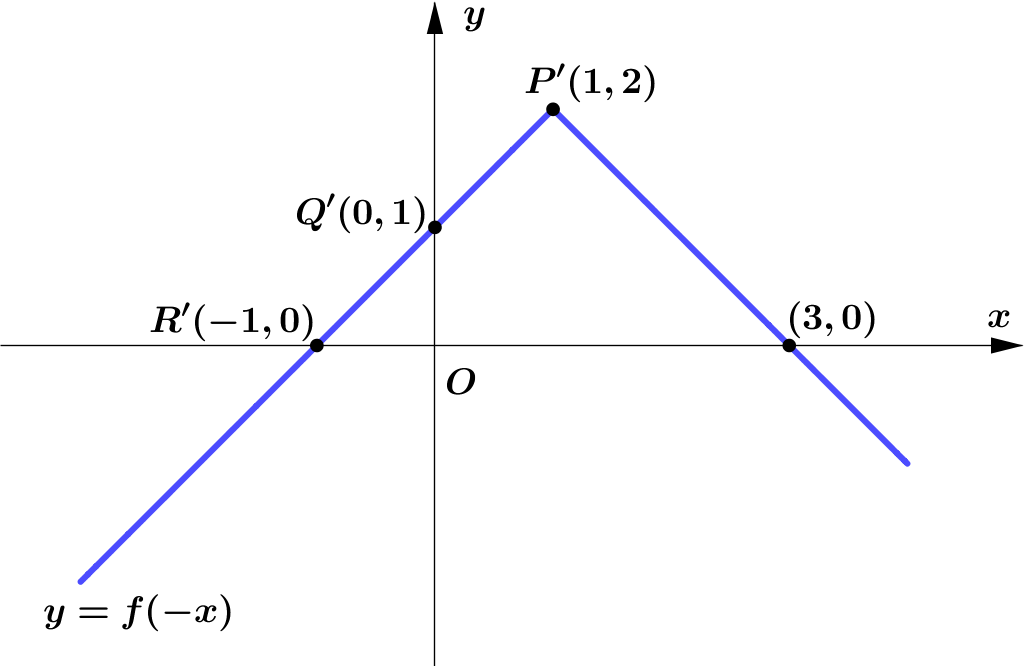
Given that $f(x)=2-|x+1|, x \in \mathbb{R}$.

Figure 3 shows the graph of $y=f(x)$.

$P$ is the vertex of the graph.The graph cuts the $y$-axis at the point $Q$ and the $x$-axis at the points $(-3,0)$ and $R$.

(a) Find the coordinates of the points $P, Q$ and $R$.

Sketch, on separate diagrams showing the corresponding vertex, $x$ and $y$-intercepts, the graphs of

(b) $y=|f(x)|$,

(c) $y=f(-x)$.

(d) Solve $f(x)=\dfrac{1}{2} x$.

$\textbf{(a)} \quad$ $f(x)=2-|x+1|$ $P$ is the vertex of the graph $y=2-|x+1|$. $\therefore\ $ The coordinate of the point $P$ is $(-1, 2)$. $Q$ is the $y$-intercept of the graph $y=2-|x+1|$. $\begin{aligned} &\\ \therefore\ \text{when } x&= 0\\\\ y&=2-|0+1|\\\\ &=1\\\\ \end{aligned}$ $\therefore\ $ The coordinate of the point $Q$ is $(0, 1)$. $R$ is the positive $x$-intercept of the graph $y=2-|x+1|$. $\begin{aligned} &\\ \therefore\ \text{when } y= 0\\\\ 0 &=2-|x+1|\\\\ |x+1|&=2 x+1 &=\pm 2 \therefore\ x+1 &=-3 \text{ or } x&=1\\\\ \end{aligned}$ $\therefore\ $ The coordinate of the point $R$ is $(1, 0)$. $\textbf{(b)} \quad$ On the graph $y=|f(x)|$, All points are unchanged. $\textbf{(c)} \quad$ On the graph $y=f(-x)$, $\begin{aligned} &\\ \quad\quad &(-3, 0)\rightarrow (3, 0)\\\\ &(-1, 2)\rightarrow (1, 2)\\\\ &(0, 1)\rightarrow (0, 1)\\\\ &(1, 0)\rightarrow (-1, 0)\\\\ \end{aligned}$ $\begin{aligned} &\\ \textbf{(d)} \quad\quad f(x) &=\frac{1}{2} x \\\\ 2-|x+1| &=\frac{1}{2} x \\\\ |x+1| &=2-\frac{1}{2} x \\\\ \therefore\ -(x+1) &=2-\frac{1}{2} x \ \text { or }\\\\ x+1&=2-\frac{1}{2} x \\\\ \therefore x &=-6 \ \text { or }\ x=\frac{2}{3} \end{aligned}$

Question 4

Figure 4

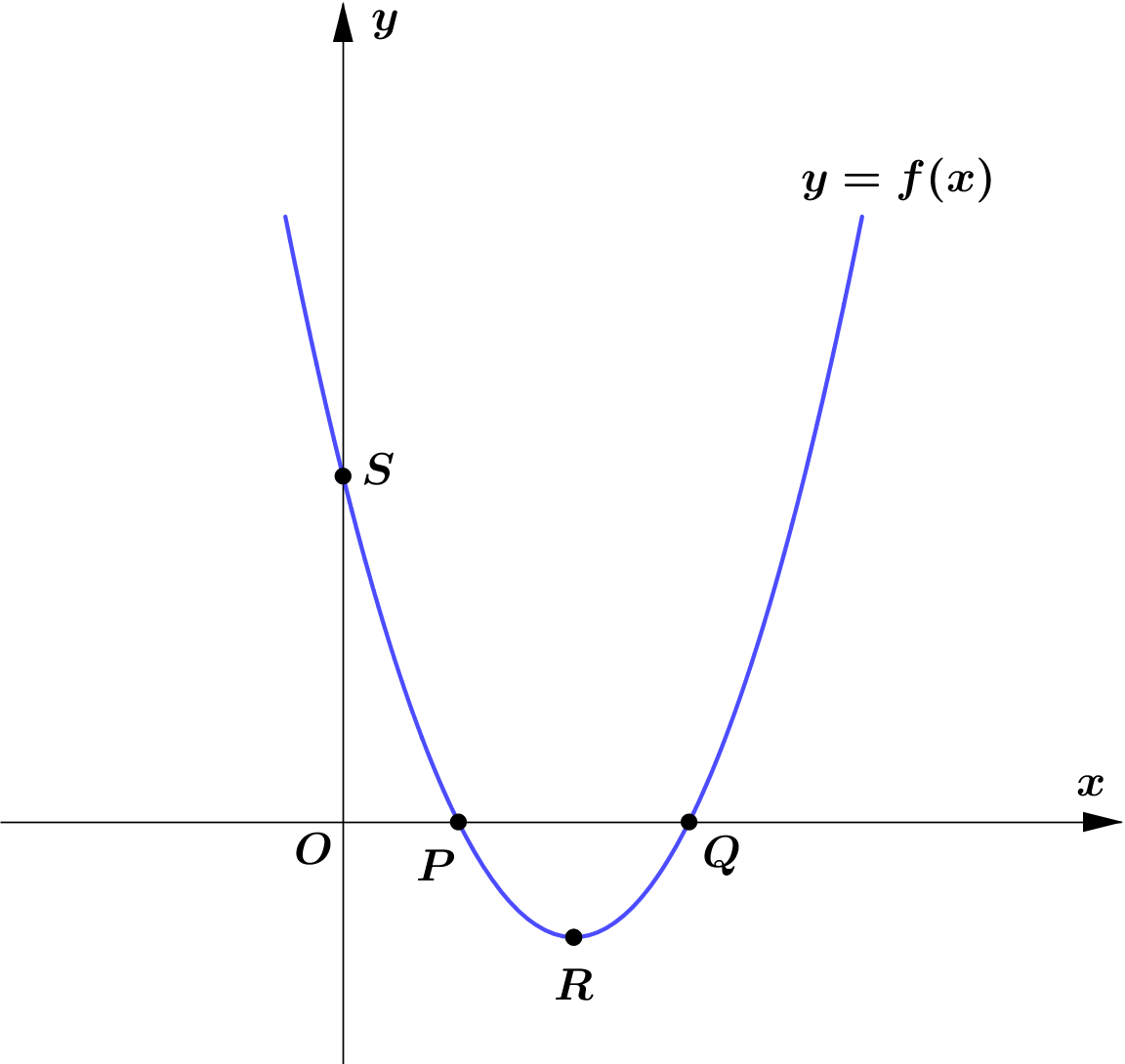
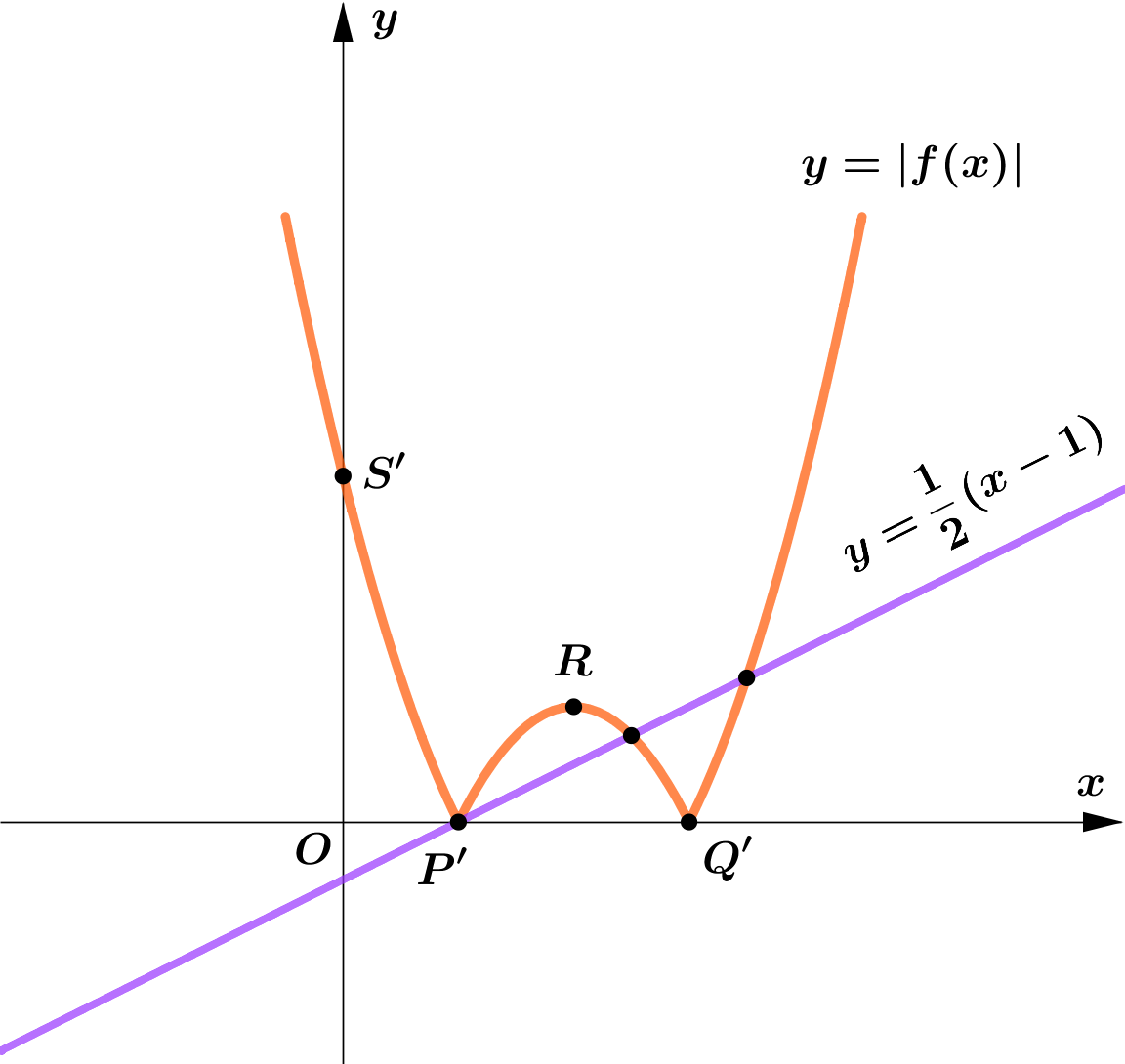
Given that $f(x)=(x-2)^2-1, x \in \mathbb{R}$.

Figure 4 shows the graph of $y=f(x)$.

$R$ is the vertex of the graph.The graph cuts the coordinate axes at the points $P, Q$ and $S$.

(a) Find the coordinates of the points $P, Q, R$ and $S$.

(b) Sketch, the graph of $y=|f(x)|$ and $y=\dfrac{1}{2}(x-1)$ in the same plane.

(c) Hence or otherwise, find the the number of solutions of $|(x-2)^2-1|=\dfrac{1}{2}(x-1)$.

$\textbf{(a)} \quad$ $f(x)=(x-2)^2-1$ $R$ is the vertex of the graph $y=(x-2)^2-1$. $\therefore\ $ The coordinate of the point $R$ is $(2, -1)$. $S$ is the $y$-intercept of the graph $y=(x-2)^2-1$. $\begin{aligned} &\\ \therefore\ \text{when } x&= 0\\\\ y&=(0-2)^2-1\\\\ &=3\\\\ \end{aligned}$ $\therefore\ $ The coordinate of the point $S$ is $(3, 0)$. $P$ and $Q$ are the $x$-intercepts of the graph $y=(x-2)^2-1$. $\begin{aligned} &\\ \therefore\ \text{when } y= 0\\\\ 0 &=y=(x-2)^2-1\\\\ (x-2)^2&=1 x-2 &=\pm 1 \therefore\ x=1 \text{ or } x&=3\\\\ \end{aligned}$ $\therefore\ $ The coordinate of the point $P$ and $Q$ are $(1, 0)$ and $(3, 0)$ respectively. $\textbf{(b)} \quad$ On the graph $y=|f(x)|$, Intercept points are unchanged. The vertex is $R'(2,1)$. $\textbf{(c)} \quad$ According to the graph, there are three solutions for the equation $|(x-2)^2-1|=\dfrac{1}{2}(x-1)$.

Question 5

The functions $f$ and $g$ are defined for all real values of $x$ by

$f(x)=3 x-2 \quad \text { and } \quad g(x)=3 x+7$

Find the exact coordinates of the point at which

(a) the graph of $y=(f\circ g)(x)$ meets the $x$-axis,

(b) the graph of $y=g(x)$ meets the graph of $y=g^{-1}(x)$,

(c) the graph of $y=|f(x)|$ meets the graph of $y=|g(x)|$.

$\begin{aligned} f(x) &=3 x-2 \\\\ g(x) &=3 x+7 \\\\ \left(f_{0} g\right)(x) &=f(g(x)) \\\\ &=f(3 x+7) \\\\ &=3(3 x+7)-2 \\\\ &=9 x+19\\\\ \end{aligned}$ When the graph of $y=(f \circ g)(x)$ meets the $x$-axis, $\begin{aligned} &\\ &9 x+19=0 \\\\ &x=-\frac{19}{9}\\\\ \end{aligned}$ The graph of $y=(f \circ g)(x)$ meets $x$-axis at $(-19 / 9, 0)$. $\begin{aligned} &\\ \text { Let } g^{-1}(x) &=p \\\\ g(p) &=x \\\\ 3 p+7 &=x \\\\ p &=\frac{x-7}{3} \\\\ g^{-1}(x) &=\frac{x-7}{3}\\\\ \end{aligned}$ When $y=g(x)$ meets $y=g^{-1}(x)$, $\begin{aligned} &\\ 3 x+7 &=\frac{x-7}{3} \\\\ 9 x+2 &=x-7 \\\\ 8 x &=-28 \\\\ x &=-\frac{7}{2} \\\\ \therefore\ y &=3\left(-\frac{7}{2}\right)+7 \\\\ &=-\frac{7}{2} \\\\ \end{aligned}$ $\therefore\ y =g(x)$ intersects y=g^{-1}(x) at $\left(-\dfrac{7}{2},-\dfrac{7}{2}\right)$. $\begin{aligned} &\\ &y=|f(x)|=|3 x-2| \\\\ &y=|g(x)|=|3 x+7|\\\\ \end{aligned}$ When $y=|f(x)|$ meets $y=|g(x)|$, $\begin{aligned} &\\ |f(x)| &=|g(x)| \\\\ |3 x-2| &=|3 x+7| \\\\ 3 x-2 &=-3 x-7 \text { or } 3 x-2=3 x+7 \\\\ 6 x &=-5 \quad(\text { impossible) }\\\\ x &=-\frac{5}{6} \\\\ \therefore\ y &=\left|3\left(-\frac{5}{6}\right)-2\right|=\frac{9}{2}\\\\ \end{aligned}$ $\therefore$ The point of intersection of $y=|f(x)|$ and $y=|g(x)|$ is $\left(-\dfrac{5}{6}, \dfrac{9}{2}\right)$.

Question 6

Figure 5

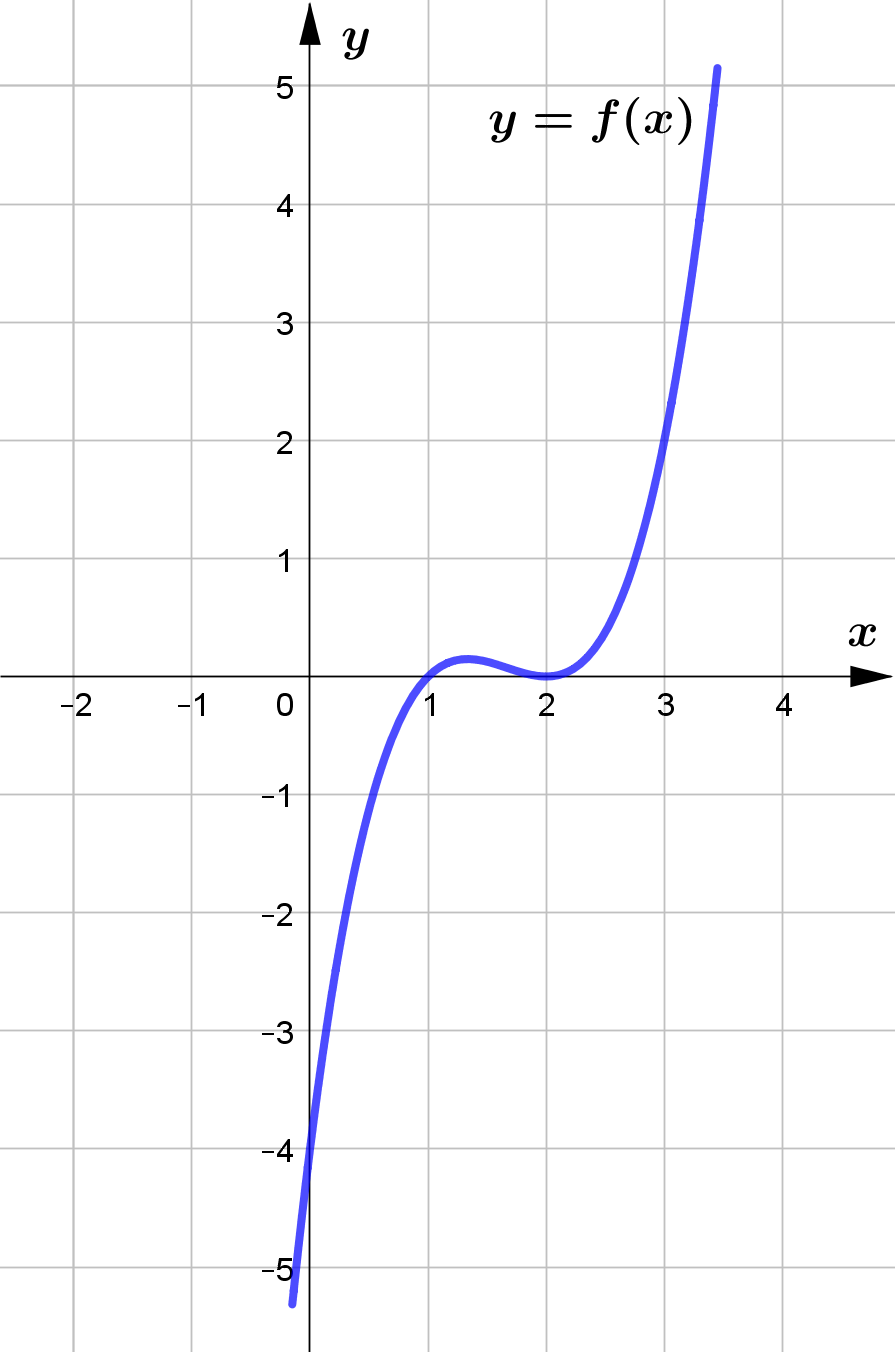
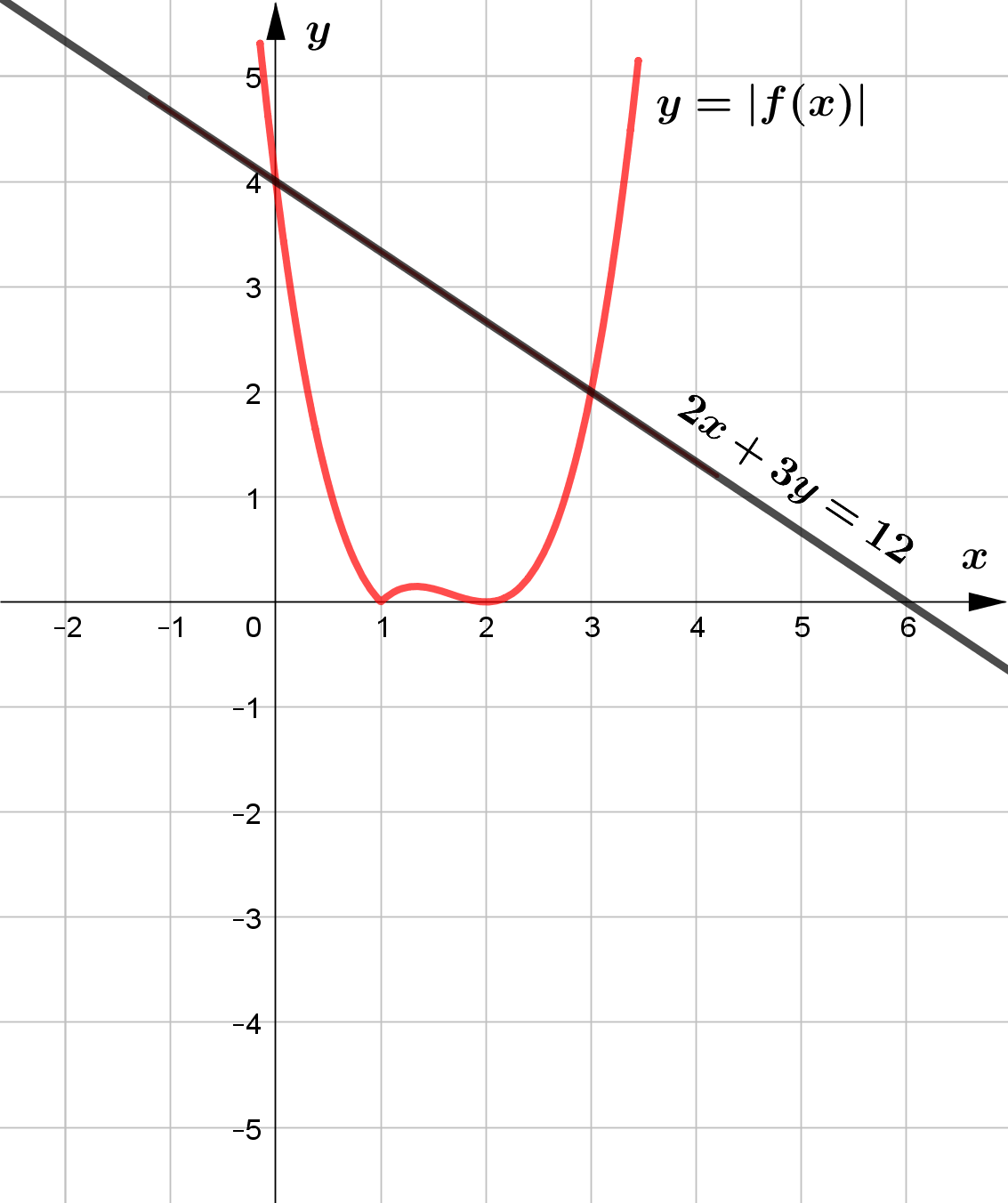
Given that $f(x)=(x-2)^2(x-1), x \in \mathbb{R}$.

Figure 5 shows part of the graph of $y=f(x)$.

(a) Sketch, the graph of $y=|f(x)|$ and $2x+3y=12$ in the same plane showing the points of intersection of the two graphs.

(b) Hence or otherwise, find the solution set of the inequality $|(x-2)^2(x-1)|\le 4-\dfrac{2}{3}x$.

According to the graph the solution set of the inequality $|(x-2)^2(x-1)|\le 4-\dfrac{2}{3}x$ is $\{x\mid 0\le x \le 3, x\in \mathbb{R}\}$

စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!