-
(a) On the axes, draw the graphs of $y=5+|3 x-2|$ and $y=11-x$. [4]
(b) Using the graphs, or otherwise, solve the inequality $11-x < 5+|3 x-2|$. [2] -
(a) Expand $(2-3x)^4$, evaluating all of the coefficients. [4]
(b) The sum of the first three terms in ascending powers of $x$ in the expansion of $(2-3 x)^{4}\left(1+\dfrac{a}{x}\right)$ is $\dfrac{32}{x}+b+c x$, where $a, b$ and $c$ are integers. Find the values of each of $a, b$ and $c .$ [4]
-
(a) Show that $\dfrac{1}{\sec x-1}+\dfrac{1}{\sec x+1}=2 \cot x \operatorname{cosec} x$. [4]
(b) Hence solve the equation $\dfrac{1}{\sec x-1}+\dfrac{1}{\sec x+1}=3 \sec x$ for $0^{\circ} < x < 360^{\circ}$. [4] -
(a) Find the $x$-coordinates of the stationary points on the curve $y=3 \ln x+x^{2}-7 x$, where $x>0$. [5]
(b) Determine the nature of each of these stationary points. [3] -
(a) Solve the following simultaneous equations.
$\begin{aligned} &\\ \qquad e^{x}+e^{y}&=5 \\\\ \qquad 2 e^{x}-3 e^{y}&=8 \end{aligned}$
[5]
(b) Solve the equation $e^{(2 t-1)}=5 e^{(5 t-3)}.$ [4] -
DO NOT USE A CALCULATOR IN THIS QUESTION.
All lengths in this question are in centimetres.
You may use the following trigonometrical ratios.
$\begin{aligned} &\\ \qquad &\sin 60^{\circ}=\dfrac{\sqrt{3}}{2} \\\\ \qquad &\cos 60^{\circ}=\dfrac{1}{2} \\\\ \qquad &\tan 60^{\circ}=\sqrt{3}\\\\ \end{aligned}$
The diagram shows triangle $A B C$ with $A C=\sqrt{6}-\sqrt{2}, A B=\sqrt{6}+\sqrt{2}$ and angle $C A B=60^{\circ}$.
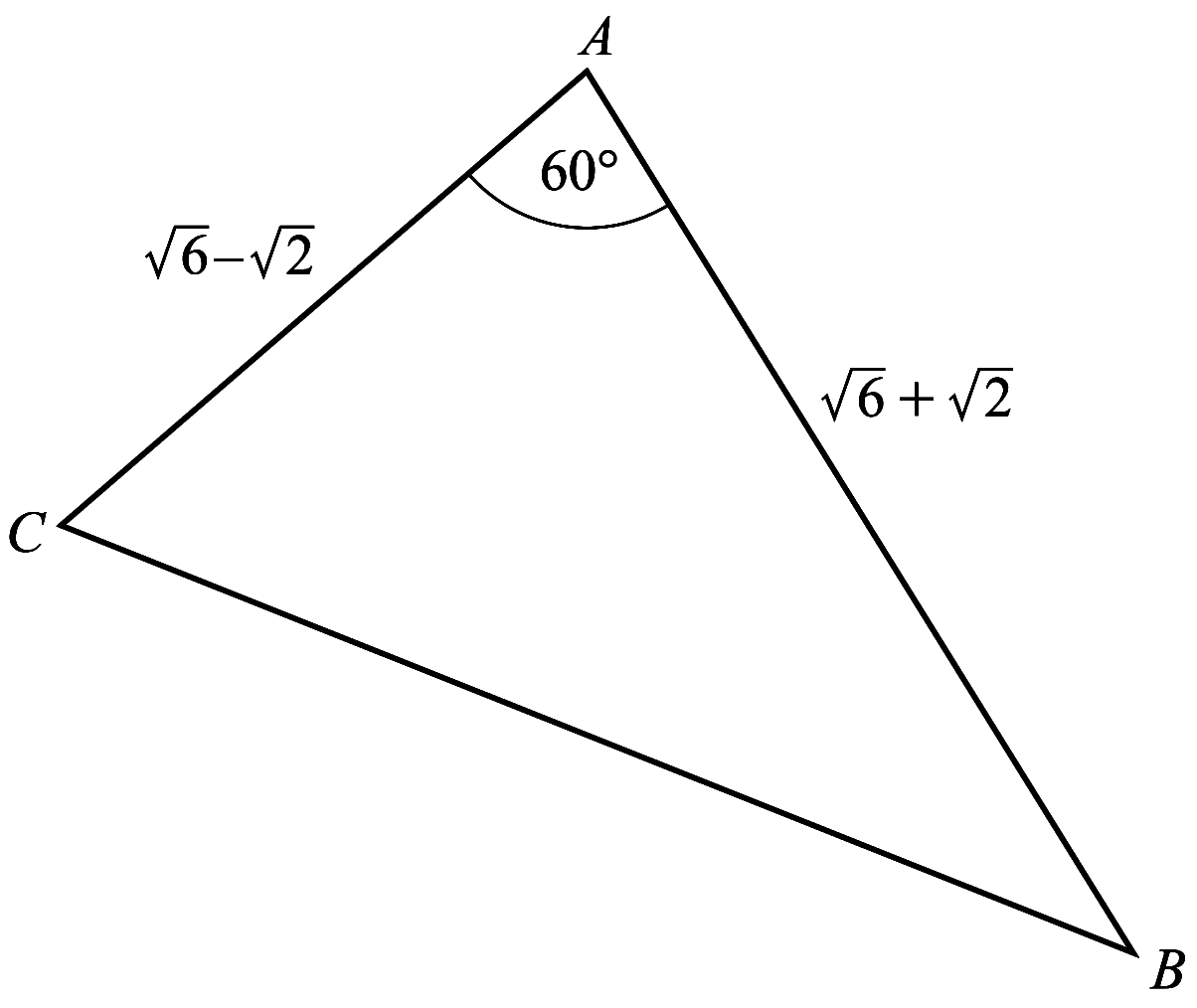
(a) Find the exact length of $B C$. [3]
(b) Show that $\sin A C B=\dfrac{\sqrt{6}+\sqrt{2}}{4}$. [2]
(c) Show that the perpendicular distance from $A$ to the line $B C$ is $1$. [2] -
It is given that $\dfrac{d^{2} y}{dx^{2}}=e^{2 x}+\dfrac{1}{(x+1)^{2}}$ for $x>-1$.
(a) Find an expression for $\dfrac{dy}{dx}$ given that $\dfrac{d y}{dx}=2$ when $x=0$. [3]
(b) Find an expression for $y$ given that $y=4$ when $x=0$. [3]
-
Variables $x$ and $y$ are such that when $\sqrt{y}$ is plotted against $\log _{2}(x+1)$, where $x>-1$, a straight line is obtained which passes through $(2,10.4)$ and $(4,15.4)$.
(a) Find $\sqrt{y}$ in terms of $\log _{2}(x+1)$. [4]
(b) Find the value of $y$ when $x=15$. [1]
(c) Find the value of $x$ when $y = 25$. [3] -
(a) Find the equation of the normal to the curve $y=x^{3}+x^{2}-4 x+6$ at the point $(1,4)$. [5]
(b) DO NOT USE A CALCULATOR IN THIS QUESTION.
Find the exact $x$-coordinate of each of the two points where the normal cuts the curve again. [5] -
(a) The first three terms of an arithmetic progression are $x, 5x-4$ and $8x+2$. Find $x$ and the common difference. [4]
(b) The first three terms of a geometric progression are $y, 5y-4$ and $8y+2$.
(i)) Find the two possible values of $y$. [4]
(ii)) For each of these values of $y$, find the corresponding value of the common ratio. [2]
2021 (Oct-Nov) CIE (4037-Additional Mathematics), Paper 2/22 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!


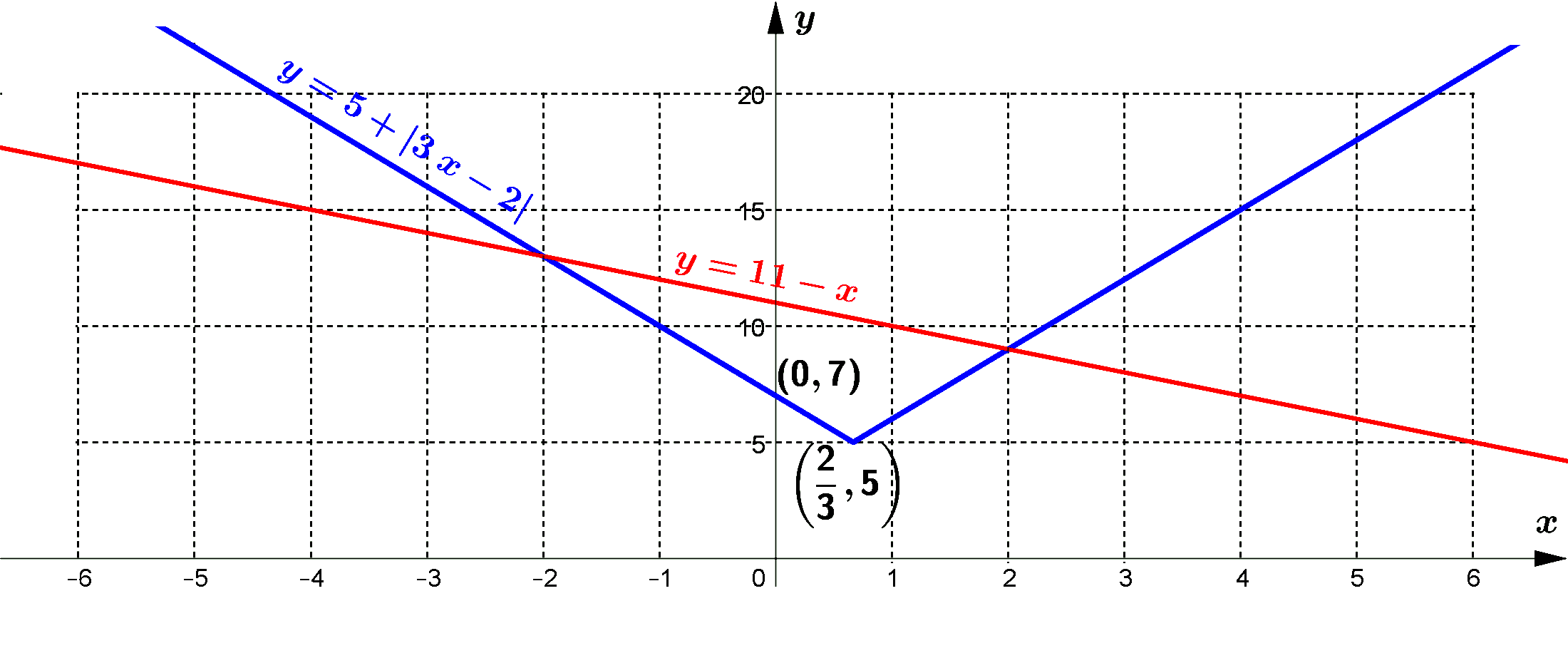 According to the graph, the solution set to satisfy the inequality $1-x < 5+| 3 x-2|$ is $\{x \mid x <-2 \text { or } x>2\}$.
According to the graph, the solution set to satisfy the inequality $1-x < 5+| 3 x-2|$ is $\{x \mid x <-2 \text { or } x>2\}$.