-
The diagram shows the graph of the cubic function $y = f( x )$. The intercepts of the curve with the axes are all integers.
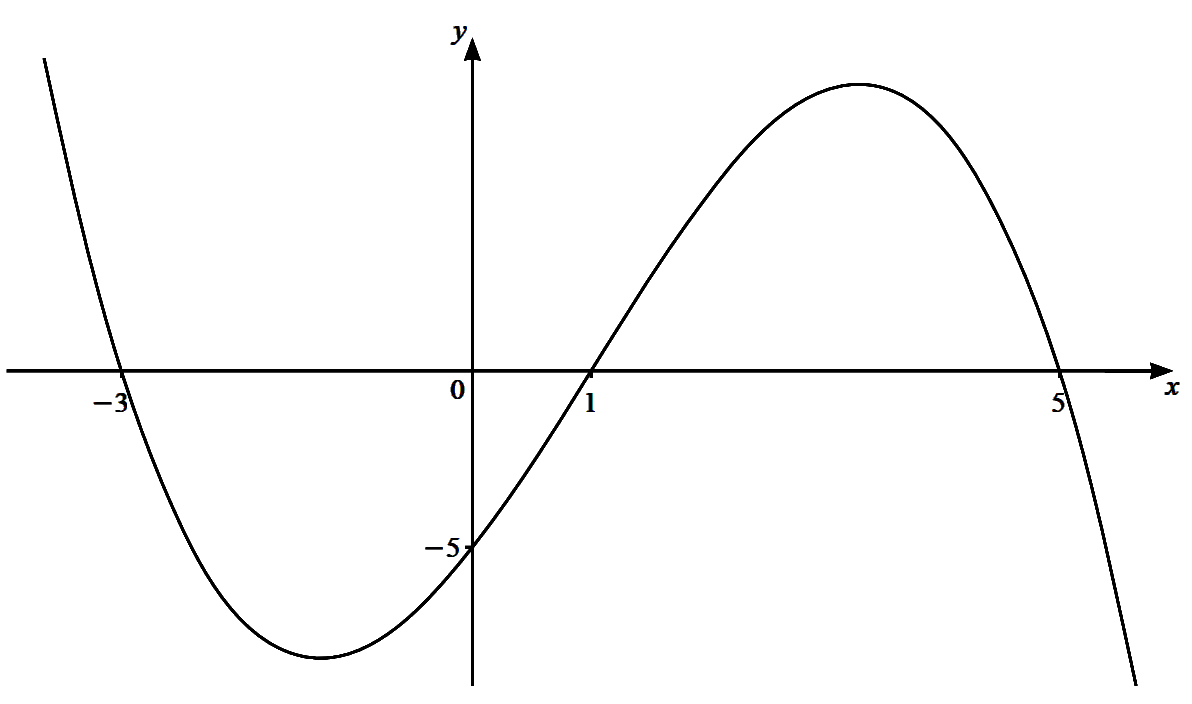
(a) Find the set of values of $x$ for which $f(x) < 0$. [1]
(b) Find an expression for f(x). [3] -
(a) Given that $\dfrac{\sqrt[3]{x y}(z y)^{2}}{(x z)^{-3} \sqrt{z}}=x^{a} y^{b} z^{c}$, find the exact values of the constants $a, b$ and $c$. [3]
(b) Solve the equation $5\left(2^{2 p+1}\right)-17\left(2^{p}\right)+3=0$. [4]
-
(a) Write $3+2 \lg a-4 \lg b$ as a single logarithm to base $10$ . [4]
(b) Solve the equation $3 \log _{a} 4+2 \log _{4} a=7$. [5] -
Solve the equation $\cot \left(2 x+\dfrac{\pi}{3}\right)-\sqrt{3}=0$, where $-\pi<x<\pi$ radians. Give your answers in terms of $\pi$. [4]
-
Find the possible values of the constant $c$ for which the line $y=c$ is a tangent to the curve $y=5 \sin \dfrac{x}{3}+4$. [3]
-
DO NOT USE A CALCULATOR IN THIS QUESTION.
The polynomial $\mathrm{p}(x)=10 x^{3}+a x^{2}-10 x+b$, where $a$ and $b$ are integers, is divisible by $2 x+1$. When $\mathrm{p}(x)$ is divided by $x+1$, the remainder is $-24$.
(a) Find the value of $a$ and of $b$. [4]
(b) Find an expression for $p(x)$ as the product of three linear factors. [4]
(c) Write down the remainder when $p(x)$ is divided by $x$. [1] -
(a)The diagram shows triangle $O A C$, where $\overrightarrow{O A}=\mathbf{a}, \overrightarrow{O B}=\mathbf{b}$ and $\overrightarrow{O C}=\mathbf{c}$. The point $B$ lies on the line $A C$ such that $A B: B C=m: n$, where $m$ and $n$ are constants.
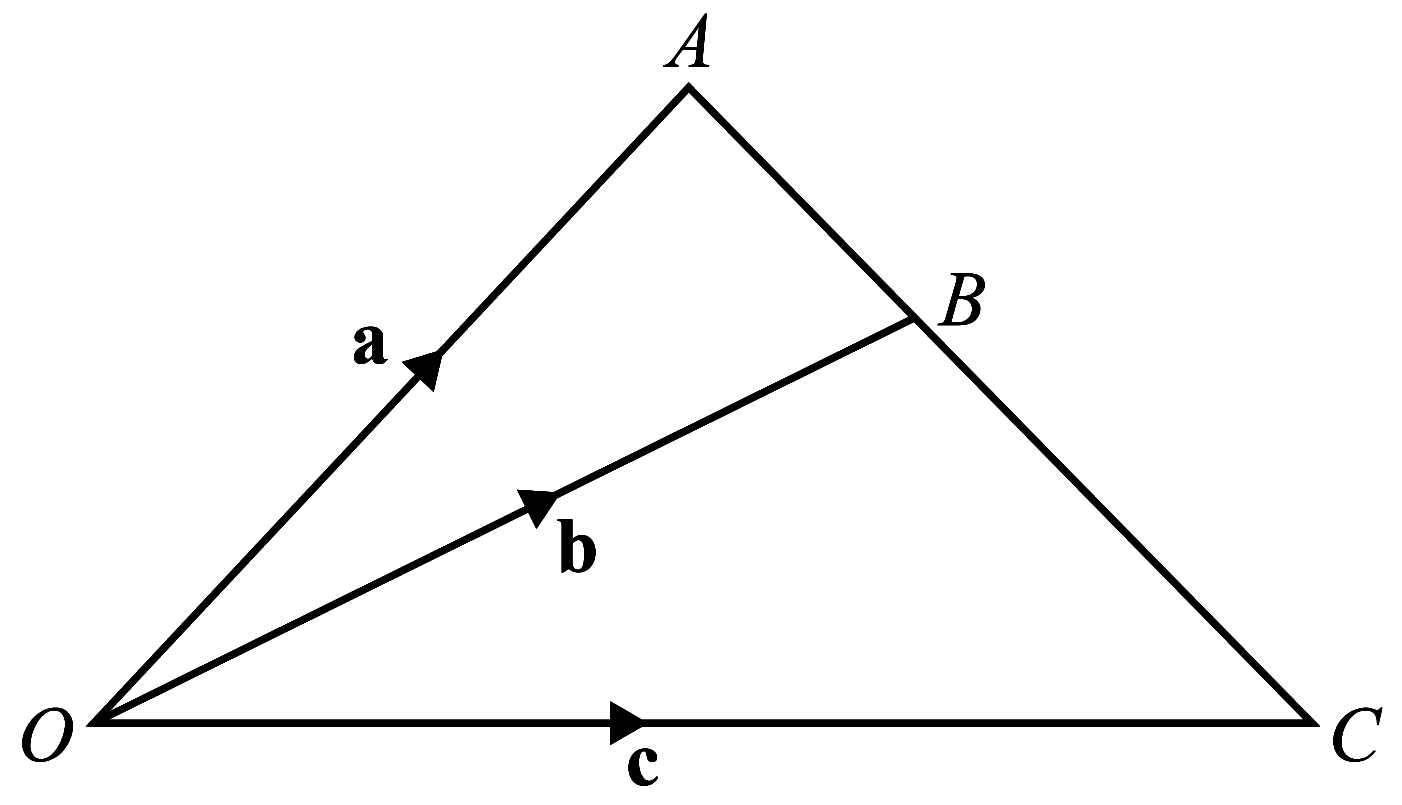
(i) Write down $\overrightarrow{A B}$ in terms of $\mathbf{a}$ and $\mathbf{b}$. [1]
(ii) Write down $\overrightarrow{B C}$ in terms of $\mathbf{b}$ and $\mathbf{c}$. [1]
(iii) Hence show that $n \mathbf{a}+m \mathbf{c}=(m+n) \mathbf{b}$. [2]
(b) Given that $\lambda\left(\begin{array}{l}2 \\ 1\end{array}\right)+(\mu-1)\left(\begin{array}{r}-4 \\ 7\end{array}\right)=(\lambda+1)\left(\begin{array}{r}4 \\ -2\end{array}\right)$, find the value of each of the constants $\lambda$ and $\mu$. [4] -
(a) A $5$-digit number is made using the digits $0, 1, 4, 5, 6, 7$ and $9$. No digit may be used more than once in any $5$-digit number. Find how many such $5$-digit numbers are even and greater than $50, 000$. [3]
(b) The number of combinations of n objects taken $4$ at a time is equal to $6$ times the number of combinations of $n$ objects taken $2$ at a time. Calculate the value of $n$. [5] -
The diagram shows a circle, centre $O$, radius $12 \mathrm{~cm}$, and a rectangle $A B C D$. The diagonals $A C$ and $B D$ intersect at $O$. The sides $A B$ and $A D$ of the rectangle have lengths $6 \mathrm{~cm}$ and $4 \mathrm{~cm}$ respectively. The points $M$ and $N$ lie on the circumference of the circle such that $M A C$ and $N D B$ are straight lines.
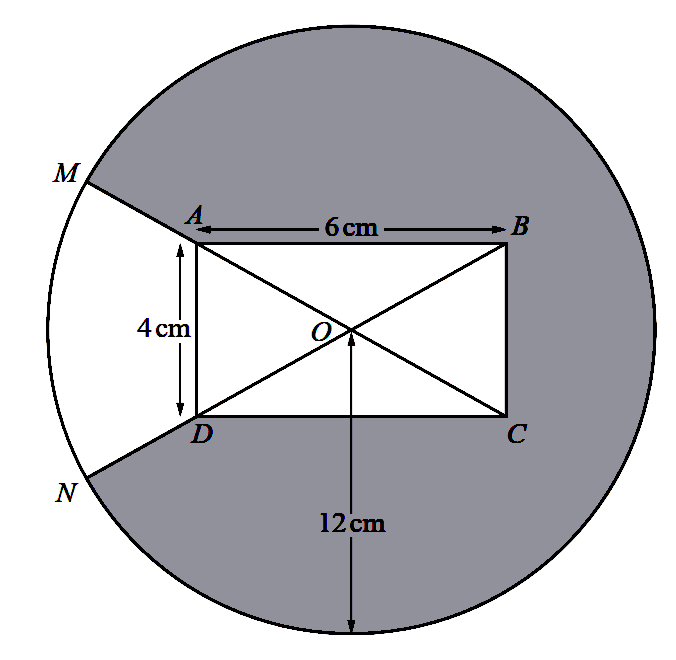
(a) Show that angle $A O D$ is $1.176$ radians correct to 3 decimal places. [2]
(b) Find the perimeter of the shaded region. [4]
(c) Find the area of the shaded region. [3]
-
The diagram shows the graph of the curve $y=\dfrac{1}{(x+2)^{2}}+\dfrac{3}{(x+2)}$ for $x>-2$. The points $A$ and $B$ lie on the curve such that the $x$-coordinates of $A$ and of $B$ are $-1$ and 2 respectively.
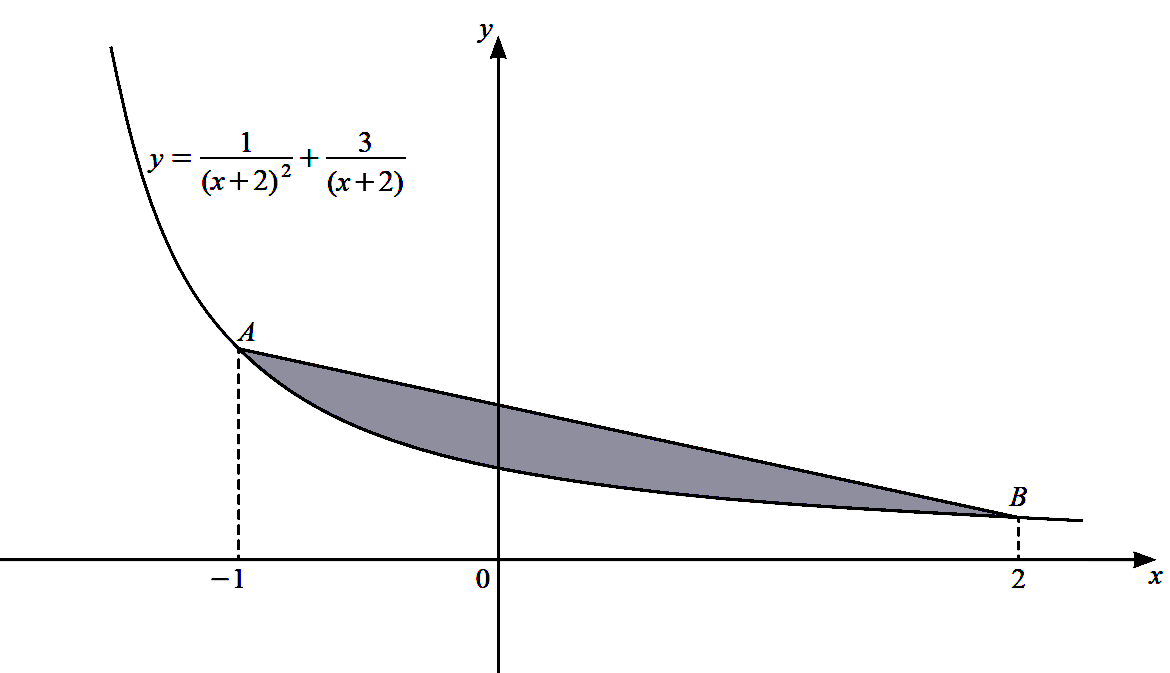
(a) Find the exact $y$-coordinates of $A$ and of $B$. [2]
(b) Find the area of the shaded region enclosed by the line $A B$ and the curve, giving your answer in the form $\dfrac{p}{q}-\ln r$, where $p, q$ and $r$ are integers. [6]
2021 (Oct-Nov) CIE (4037-Additional Mathematics), Paper 1/12 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!

