Trigonometric Limits
- $\displaystyle \lim_{x \to 0} \left( {\sin x} \right)=0$
- $\displaystyle \lim_{x \to 0} \left(\cos x\right)=1$
- $\displaystyle \lim_{x \to 0} \left(\dfrac{\sin x}{x}\right)=1$
ဖော်ပြပါပုံသေနည်း များဖြစ်ပေါ်လာပုံကို ဒီနေရာမှာ ဖတ်ပါ။
Derivative of $\sin x$ and $\cos x$ from first principles
အထက်ဖော်ပြပါ limit များကို အသုံးချ၍ $\sin x$ နှင့် $\cos x$ ၏ derivatives များကို အောက်ပါအတိုင်း ရှာယူနိုင်ပါသည်။
|
$$\begin{aligned}
y &=\sin x \\\\
y+\delta y &=\sin (x+\delta x) \\\\
\delta y &=(y+\delta y)-y \\\\
&=\sin (x+\delta x)-\sin x \\\\
&=2 \cos \frac{x+\delta x+x}{2} \sin \frac{x+\delta x-x}{2} \\\\
\frac{\delta y}{\delta x} &=\frac{2}{\delta x} \cos \left(x+\frac{\delta x}{2}\right) \sin \frac{\delta x}{2} \\\\
&=\cos \left(x+\frac{\delta x}{2}\right) \frac{\sin \frac{\delta x}{2}}{\frac{\delta x}{2}} \\\\
\frac{d y}{d x} &=\lim _{\delta x \rightarrow 0} \frac{\delta y}{\delta x} \\\\
&=\lim _{\delta x \rightarrow 0}\left[\cos \left(x+\frac{\delta x}{2}\right) \cdot \frac{\sin \frac{\delta x}{2}}{\frac{\delta x}{2}}\right] \\\\
&=\cos (x+0)(1) \\\\
&=\cos x
\end{aligned}$$
$$\begin{array}{|c|}
\hline
\dfrac{d}{d x}(\sin x)=\cos x\\
\hline
\end{array}$$
$$\begin{aligned}
y &=\cos x \\\\
y+\delta y &=\cos (x+\delta x) \\\\
\delta y &=(y+\delta y)-y \\\\
&=\cos (x+\delta x)-\cos x \\\\
&=-2 \sin \left(\frac{x+\delta x+x}{2}\right) \sin \left(\frac{x+\delta x-x}{2}\right) \\\\
\frac{\delta y}{\delta x} &=-\frac{2}{\delta x} \sin \left(x+\frac{\delta x}{2}\right) \sin \frac{\delta x}{2} \\\\
&=-\sin \left(x+\frac{\delta x}{2}\right) \frac{\sin \frac{\delta x}{2}}{\frac{\delta x}{2}} \\\\
\frac{d y}{d x} &=\lim _{\delta x \rightarrow 0} \frac{\delta y}{\delta x} \\\\
&=\lim _{\delta x \rightarrow 0}\left[-\sin \left(x+\frac{\delta x}{2}\right) \cdot \frac{\sin \frac{\delta x}{2}}{\frac{\delta x}{2}}\right] \\\\
&=-\sin x
\end{aligned}$$
$$\begin{array}{|c|}
\hline
\dfrac{d}{d x}(\cos x)=-\sin x\\
\hline
\end{array}$$
|
Drivative of Other Trigonometric Functions
$\sin x$ နှင့် $\cos x$ ၏ derivatives များကို သိလျှင် အခြား trigonometric fuctions များ ဖြစ်ကြသော
$\tan x, \cot x, \sec x$ နှင့် $\csc x$ တို့၏ derivatives များကို chain rule, product rule, quotient
rule များကို သုံး၍ အလွယ်တကူရှာနိုင်ပါသည်။
Derivative of $\tan x$
$$
\begin{aligned}
\frac{d}{d x}(\tan x) &=\frac{d}{d x}\left(\frac{\sin x}{\cos x}\right) \\\\
&=\frac{\cos x \frac{d}{d x}(\sin x)-\sin x \frac{d}{d x}(\cos x)}{\cos ^{2} x} \\\\
&=\frac{\cos ^{2} x+\sin ^{2} x}{\cos ^{2} x} \\\\
&=\frac{1}{\cos ^{2} x} \\\\
&=\sec ^{2} x
\end{aligned}
$$
Derivative of $\cot x$
$$\begin{aligned}
\dfrac{d}{d x}(\cot x) &=\dfrac{d}{d x}\left(\dfrac{\cos x}{\sin x}\right) \\\\
&=\dfrac{\sin x \dfrac{d}{d x}(\cos x)-\cos x \dfrac{d}{d x}(\sin x)}{\sin ^{2} x} \\\\
&=\dfrac{-\sin ^{2} x-\cos ^{2} x}{\sin ^{2} x} \\\\
&=\dfrac{-\left(\sin ^{2} x+\cos ^{2} x\right)}{\sin ^{2} x} \\\\
&=-\dfrac{1}{\sin ^{2} x} \\\\
&=-\csc^{2} x
\end{aligned}$$
Derivative of $\sec x$
$$\begin{aligned}
\frac{d}{d x}(\sec x) &=\frac{d}{d x}\left(\frac{1}{\cos x}\right) \\\\
&=-\frac{1}{\cos ^{2} x} \frac{d}{d x}(\cos x) \\\\
&=-\frac{1}{\cos ^{2} x}(-\sin x) \\\\
&=\frac{1}{\cos x} \cdot \frac{\sin x}{\cos x} \\\\
&=\sec x \cdot \tan x
\end{aligned}$$
Derivative of $\csc x$
$$\begin{aligned}
\frac{d}{d x}(\csc x) &=\frac{d}{d x}\left(\frac{1}{\sin x}\right) \\\\
&=-\frac{1}{\sin ^{2} x} \frac{d}{d x}(\sin x) \\\\
&=-\frac{1}{\sin x} \frac{\cos x}{\sin x} \\\\
&=-\csc x \cot x
\end{aligned}$$
|
Formulas for Derivatives of Trigonometric Functions
|
$$\begin{array}{|l|l|l|}
\hline 1 & \dfrac{d}{d x} \sin x=\cos x & \dfrac{d}{d x} \sin u=\cos u \dfrac{d u}{d x} \\
\hline 2 & \dfrac{d}{d x} \cos x=-\sin x & \dfrac{d}{d x} \cos u=-\sin u \dfrac{d u}{d x} \\
\hline 3 & \dfrac{d}{d x} \tan x=\sec ^{2} x & \dfrac{d}{d x} \tan u=\sec ^{2} u \dfrac{d u}{d x} \\
\hline 4 & \dfrac{d}{d x} \cot x=-\csc^{2} x & \dfrac{d}{d x} \cot u=-\csc^{2} u \dfrac{d u}{d x} \\
\hline 5 & \dfrac{d}{d x} \sec x=\sec x \tan x & \dfrac{d}{d x} \sec u=\sec u \tan u \dfrac{d u}{d x} \\
\hline 6 & \dfrac{d}{d x} \csc x=-\csc x \cot x & \dfrac{d}{d x} \csc u=-\csc u \cot u \dfrac{d u}{d x} \\
\hline
\end{array}$$
|
Problems
-
Differentiate the following with respect to $x$.
$\begin{aligned}
&\\
\text {(a) }\quad & \sin 5 x\\\\
\text {(b) }\quad & \cos \left(7 x^{2}-2\right)\\\\
\text {(c) }\quad & \tan (6 x+7)\\\\
\text {(d) }\quad & 5 \sec (3 x+1)\\\\
\text {(e) }\quad & \sin (2 x+3) \\\\
\text {(f) }\quad & \cos \left(\dfrac{3}{x}\right)\\\\
\text {(g) }\quad & x^{3} \cos 2 x\\\\
\text {(h) }\quad & \cos 7 x+\sin 3 x\\\\
\text {(i) }\quad & \dfrac{\cot (1-2 x)}{3}\\\\
\text {(j) }\quad & -2 \csc 3 x\\\\
\text {(k) }\quad & \sin x \cos 2 x\\\\
\text {(l) }\quad & \cos ^{2}(5 x)\\\\
\text {(m) }\quad & \tan ^{3} \sqrt{x}\\\\
\text {(n) }\quad & \sin (\cos x)\\\\
\text {(o) }\quad & \dfrac{\sin x}{1+\tan x}\\\\
\text {(p) }\quad & \sqrt{\sin x+\cos x}\\\\
\text {(q) }\quad & (x+\tan x)^{3}\\\\
\text {(r) }\quad & \dfrac{\tan 2 x}{1+\cot x}
\end{aligned}$
-
Find $\dfrac{d y}{d x}$.
$\begin{aligned}
&\\
\text {(a) }\quad & y=\sin^2x\\\\
\text {(b) }\quad & y=\cos \sqrt{x} \\\\
\text {(c) }\quad & y=\tan ^{2}\left(x^{2}\right) \\\\
\text {(d) }\quad & y=\sin 2x – x \cos x\\\\
\text {(e) }\quad & y=\dfrac{x}{\tan x}\\\\
\text {(f) }\quad & y=\sin x \cos ^{2} x\\\\
\text {(g) }\quad & y=\sin \left(1-x^{2}\right)\\\\
\text {(h) }\quad & y=2 \pi x+2 \cos \pi x\\\\
\text {(i) }\quad & y=\sin ^{2} x \cos {3 x}\\\\
\text {(j) }\quad & y=x^{2} \sin \left(\dfrac{1}{x}\right)\\\\
\text {(k) }\quad & 3 x^{2}+2 \sin y=y^{2}\\\\
\text {(l) }\quad & \sin x \cos y=2 y\\\\
\text {(m) }\quad & 2 x y+\sin x=3\\\\
\text {(n) }\quad & y=\dfrac{\cos (1-2 x)}{\sqrt{x}}\\\\
\text {(o) }\quad & y=\sin ^{4} x \cos (3 x)\\\\
\text {(p) }\quad & x+\sin y=\cos (x y)\\\\
\text {(q) }\quad & x+y^{2}=\sin (x+y)\\\\
\text {(r) }\quad & 2 \sin x=x+\cos y
\end{aligned}$
-
Given that $y=x \sin x$, find $\dfrac{d^{2} y}{d x^{2}}$.
-
Given that $y=\cos ^{2} x$, prove that $\dfrac{d^{2} y}{d x^{2}}+4 y=2$.
-
Given that $y=\dfrac{1}{3} \cos ^{3} x-\cos x$, prove that $\dfrac{d y}{d x}=\sin ^{3} x$.
-
If $x \cos y=\sin x$, prove that $\dfrac{d y}{d x}=\dfrac{\cos y(\cos y-\cos x)}{\sin y \sin x}$.
-
Find the value $a$ and $b$ for which $\dfrac{d}{d x}\left(\dfrac{\sin x}{2+\cos x}\right)=\dfrac{a+b \cos x}{(2+\cos x)^{2}}$.
-
Find the equation of the tangent line to the curve $y=2 \sin x-3$ at $x=\dfrac{\pi}{6}$.
-
If $y=\sin 6 x+\cos ^{2} x$, find the value of $\dfrac{d y}{d x}$ when $x=\dfrac{\pi}{3}$.
-
Given that $y=\sin 3 x+\cos ^{3} x$, find the value of $\dfrac{d y}{d x}$ when $x=\dfrac{\pi}{4}$.
-
Find the equation of tangent to the curve $y=\sin \left(\dfrac{x}{3}\right)$ at the point where $x=\pi$.
-
If $y=\sin ^{2} x$, prove that $4 y+y^{\prime \prime}=2$.
-
If $y=3 \sin 2 x+2 \cos 2 x$, prove that $4 y+y^{\prime \prime}=0$.
-
If $y=\sin 3 x-2 \cos 3 x$, prove that $\dfrac{d^{2} y}{d x^{2}}=-9 y$.
-
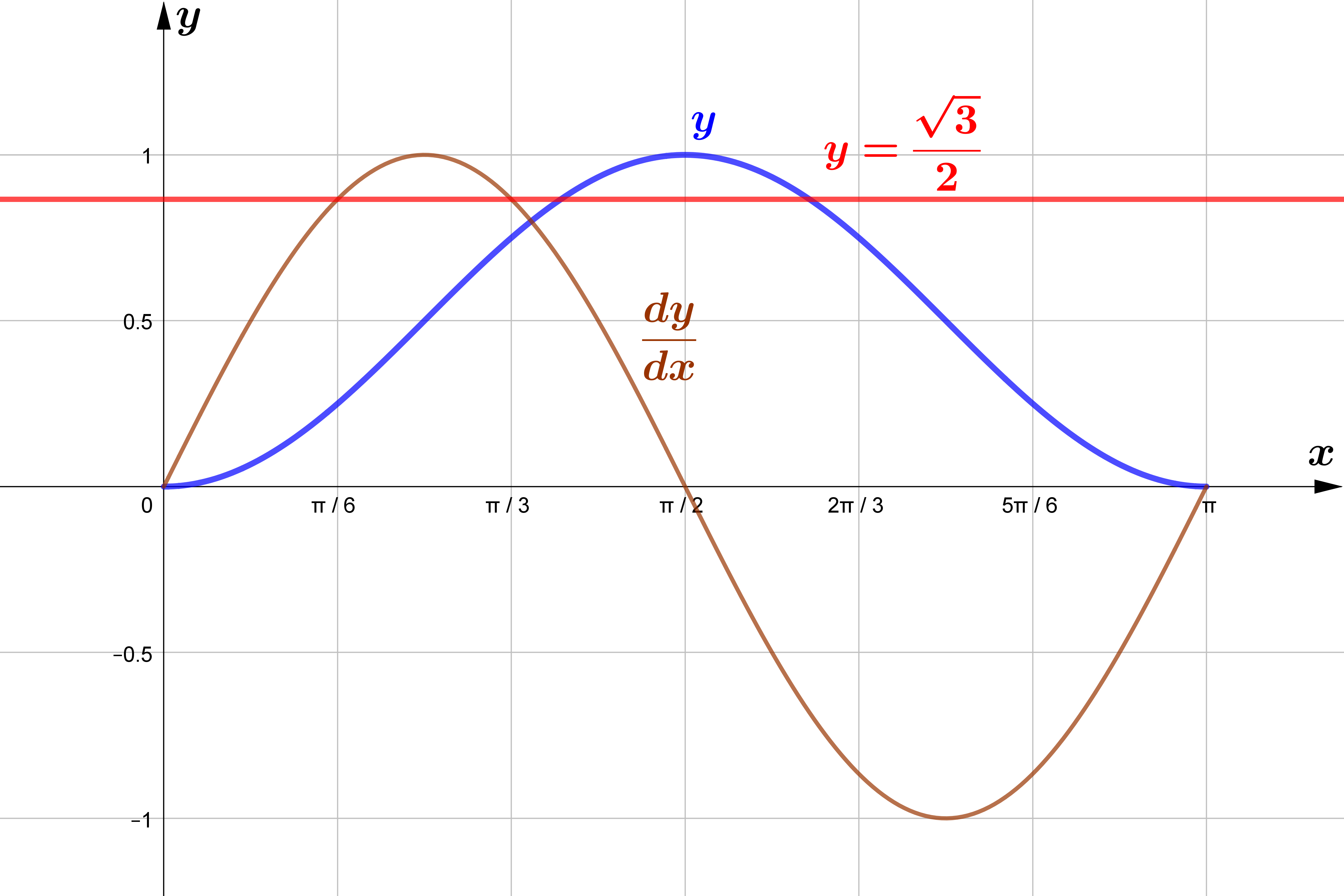
Given that $y=\sin ^{2} x$ for $0 \leqslant x \leqslant \pi$, find the exact values of the $x$-coordinates
of the points on the curve where the gradient is $\dfrac{\sqrt{3}}{2}$.
-
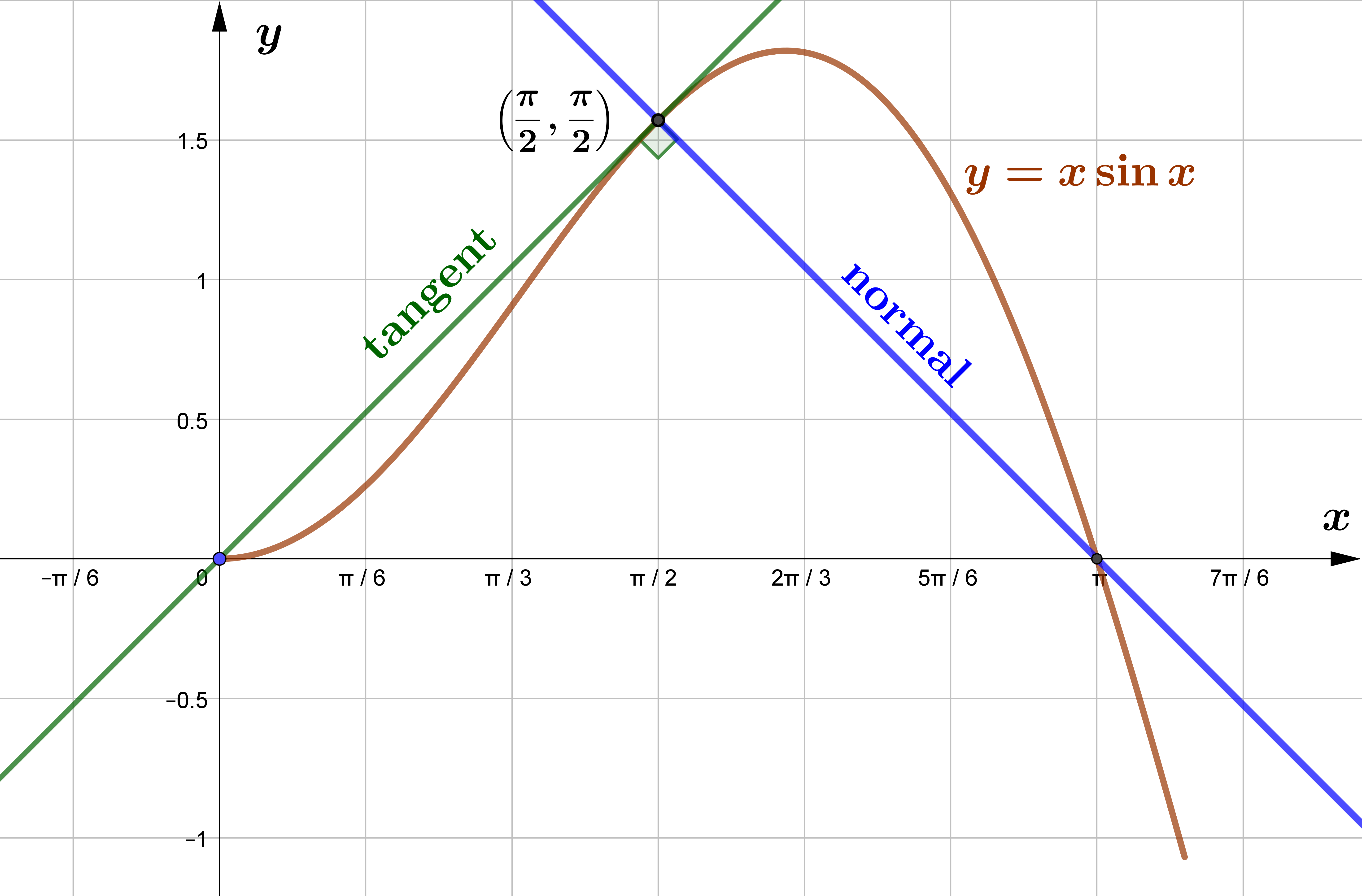
Prove that the normal to the curve $y=x \sin x$ at the point $P\left(\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$
intersects the $x$-axis at the point $(\pi, 0)$.
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!