Circle တစ်ခု၏ ဗဟို၊ အချင်းဝက်ကို သိလျှင် Circle Equation ကို ရှာယူနိုင်ကြောင်း Conic Sections တွင် တင်ပြခဲ့ပြီး ဖြစ်ပါသည်။ ယခုသင်ခန်းစာတွင် circle တစ်ခု၏ ဂုဏ်သတ္တိများကို အသုံးပြု၍ analytic geometry ဆိုင်ရာ IGCSE A Level ပုစ္ဆာများနှင့် အဖြေများကို တင်ပြထားပါသည်။
-
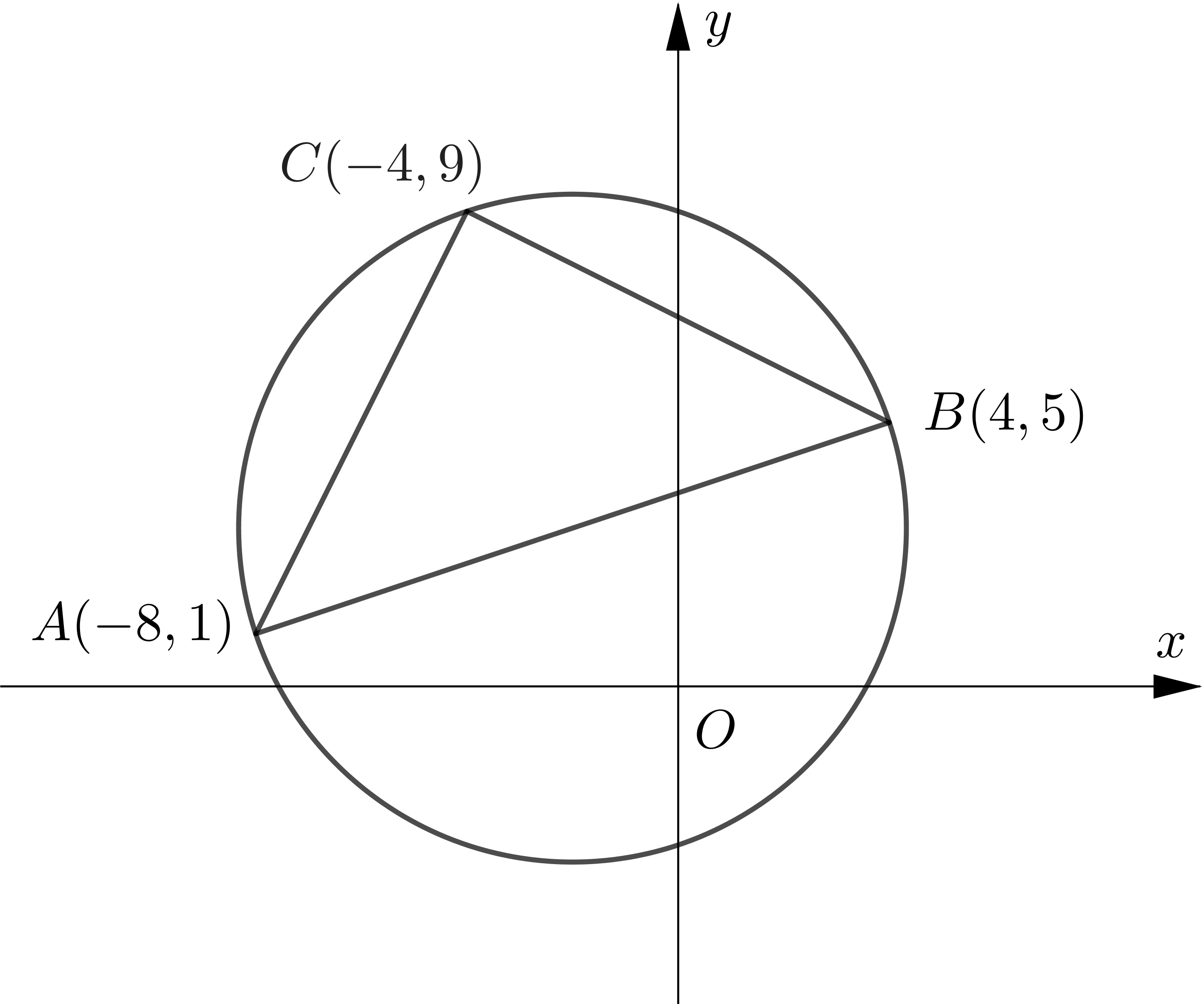
The points $A(-8,1), B(4,5)$ and $C(-4,9)$ lie on the circle, as shown in the diagram.
(a) Show that $A B$ is a diameter of the circle.
(b) Find an equation of the circle.
-
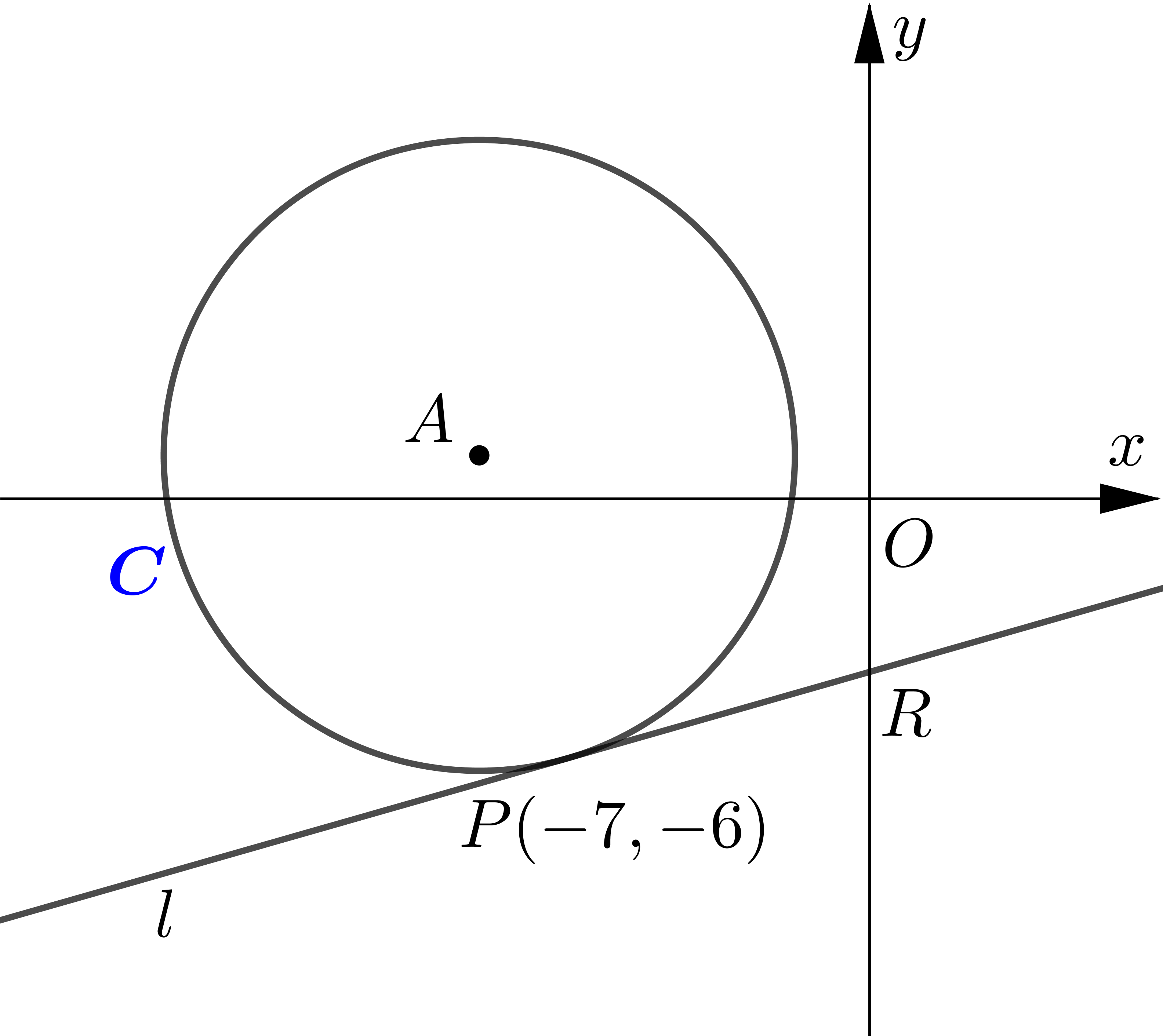
The circle $C$ has equation $x^{2}+18 x+y^{2}-2 y+29=0$.
(a) Verify the point $P(-7,-6)$ lies on $C$.
(b) Find an equation for the tangent to $C$ at the point $P$, giving your answer in the form $y=m x+b$.
(c) Find the coordinates of $R$, the point of intersection of the tangent and
(d)Find the area of the triangle $A P R$.
-
The tangent to the circle $(x+4)^{2}+(y-1)^{2}=242$ at $(7,-10)$ meets the $y$-axis at $S$ and the $x$-axis at $T$.
(a) Find the coordinates of $S$ and $T$.
(b) Hence, find the area of $\triangle O S T$, where $O$ is the origin.
-
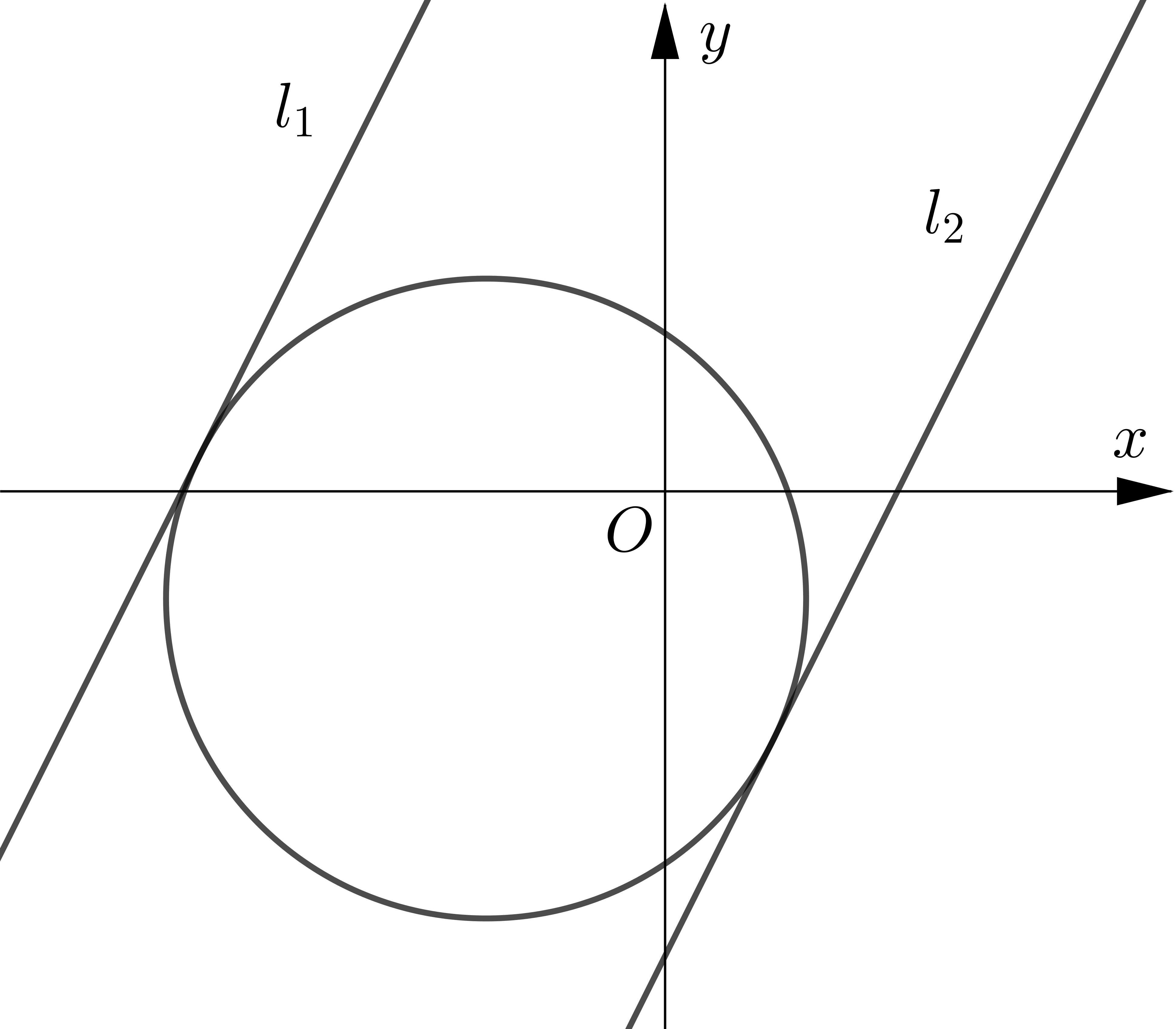
The circle $C$ has equation $(x+5)^{2}+(y+3)^{2}=80$. The line $l$ is a tangent to the circle and has gradient $2 .$ Find two possible equations for $l$ giving your answers in the form $y=m x+c$.
- The line with equation $2 x+y-5=0$ is a tangent to the circle with equation
$(x-3)^{2}+(y-p)^{2}=5$.
(a) Find the two possible values of $p$.
(b) Write down the coordinates of the centre of the circle in each case.
-
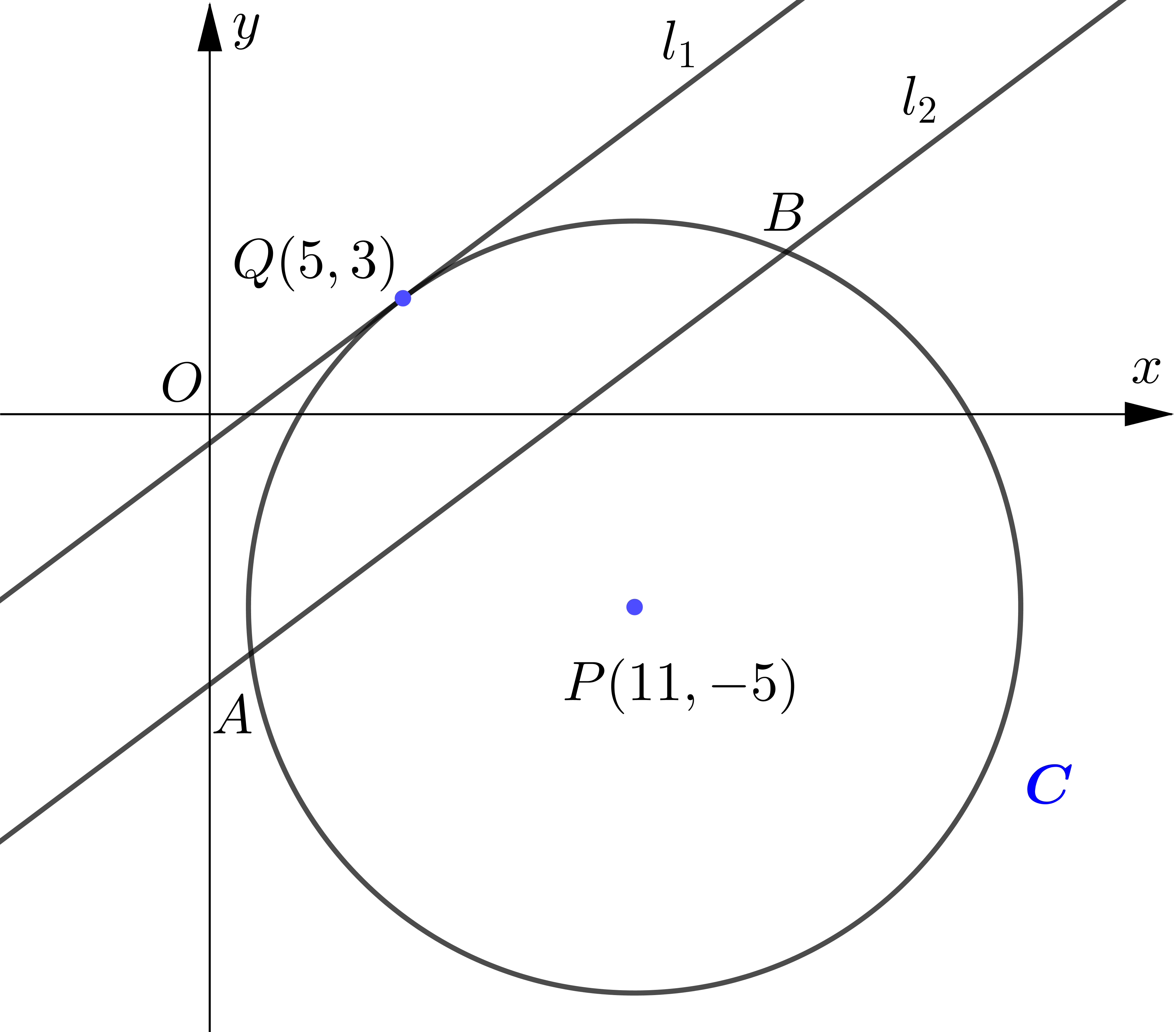
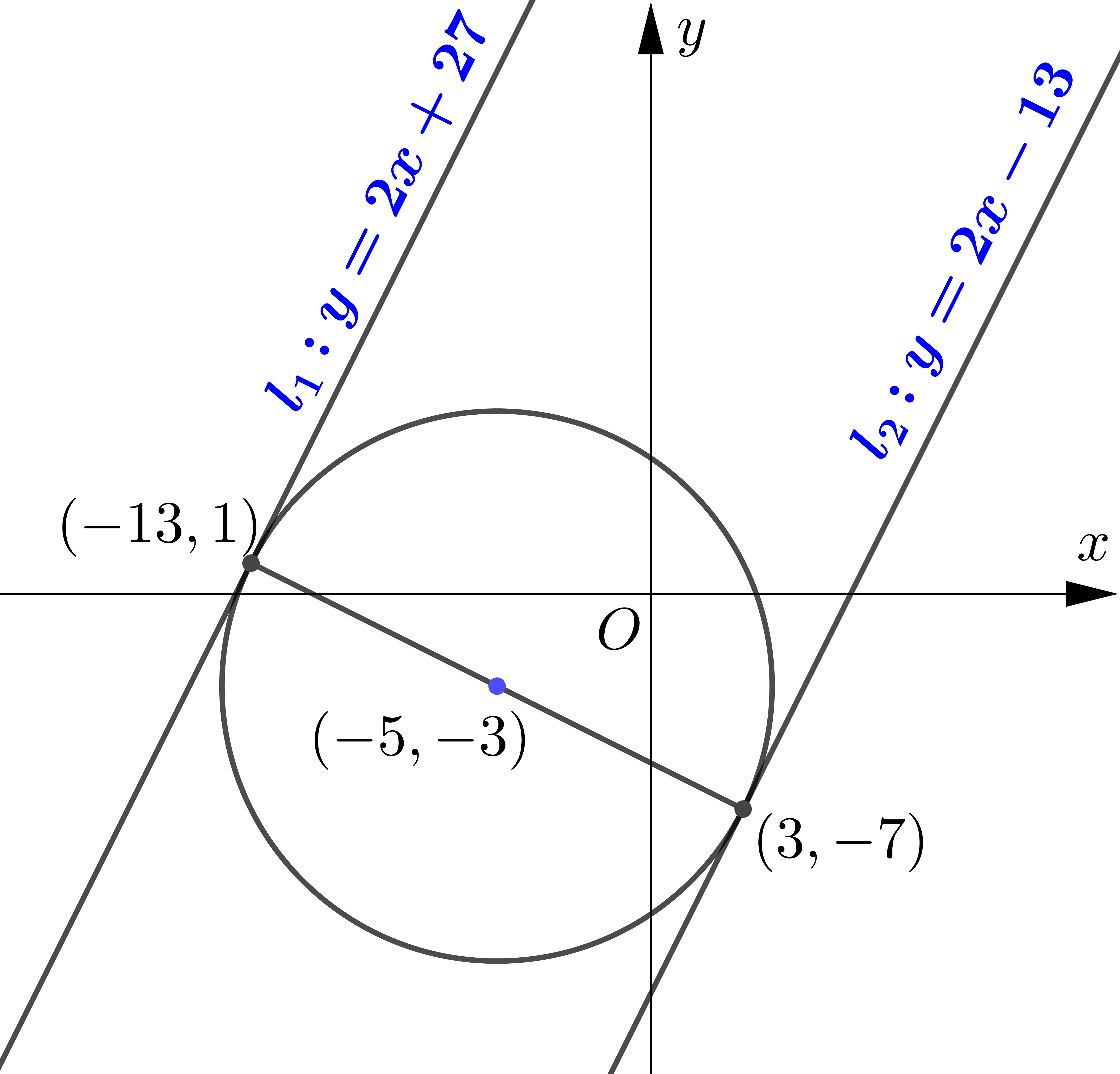
The circle $C$ has centre $P(11,-5)$ and passes through the point $Q(5,3)$.
(a) Find an equation for $C$.
The line $l_{1}$ is a tangent to $C$ at the point $Q$.
(b) Find an equation for $l_{1}$.
The line $l_{2}$ is parallel to $l_{1}$ and passes through the midpoint of $P Q .$
(c) Find the equation of $l_2$.
Given that $l_{2}$ intersects $C$ at $A$ and $B$. find the coordinates of points $A$ and $B$,
(d) find the length of the line segment $A B$, leaving your answer in its simplest surd form.
-

The points $R$ and $S$ lie on a circle with centre $C(a,-2)$, as shown in the diagram.The point $R$ has coordinates $(2,3)$ and the point $S$ has coordinates $(10,1) .$ $M$ is the midpoint of the line segment $R S .$ The line $l$ passes through $M$ and $C .$
(a) Find an equation for $l .$
(b) Find the value of $a .$
(c) Find the equation of the circle.
(d) Find the points of intersection, $A$ and $B$, of the line $l$ and the circle.
-
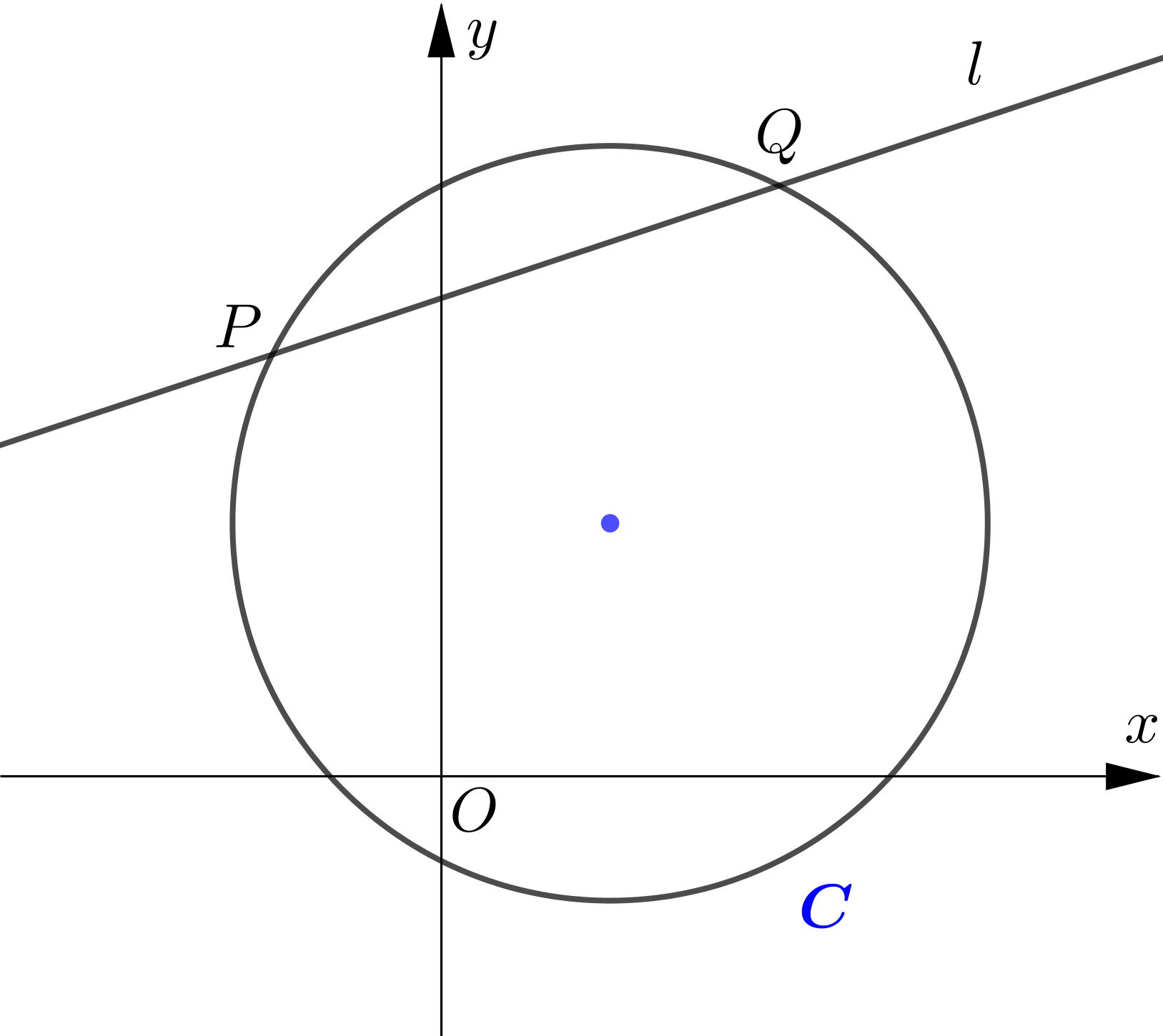
The circle $C$ has equation $x^{2}-4 x+y^{2}-6 y=7$. The line $l$ with equation $x-3 y+17=0$ intersects the circle at the points $P$ and $Q$.
(a) Find the coordinates of the point $P$ and the point $Q$.
(b) Find the equation of the tangent at the point $P$ and the point $Q$.
(c) Find the equation of the perpendicular bisector of the chord $P Q$.
(d) Show that the two tangents and the perpendicular bisector intersect at a single point and find the coordinates of the point of intersection.
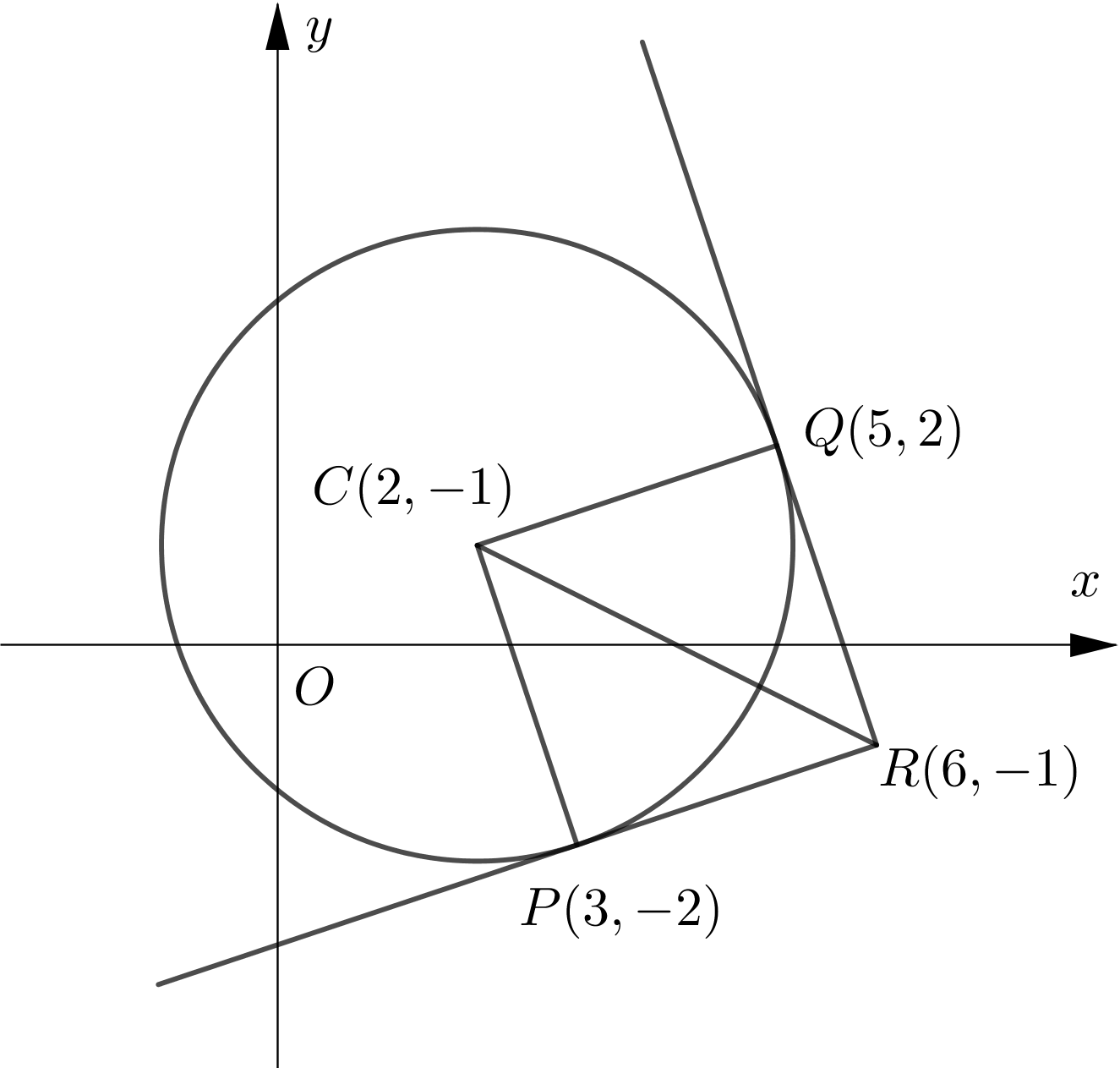
- The circle with centre $C$ has equation $(x-2)^{2}+(y-1)^{2}=10$.
The tangents to the circle at points $P$ and $Q$ meet at the point $R$ with coordinates $(6,-1)$.
(a) Show that $C P R Q$ is a square.
(b) Hence find the equations of both tangents.
-
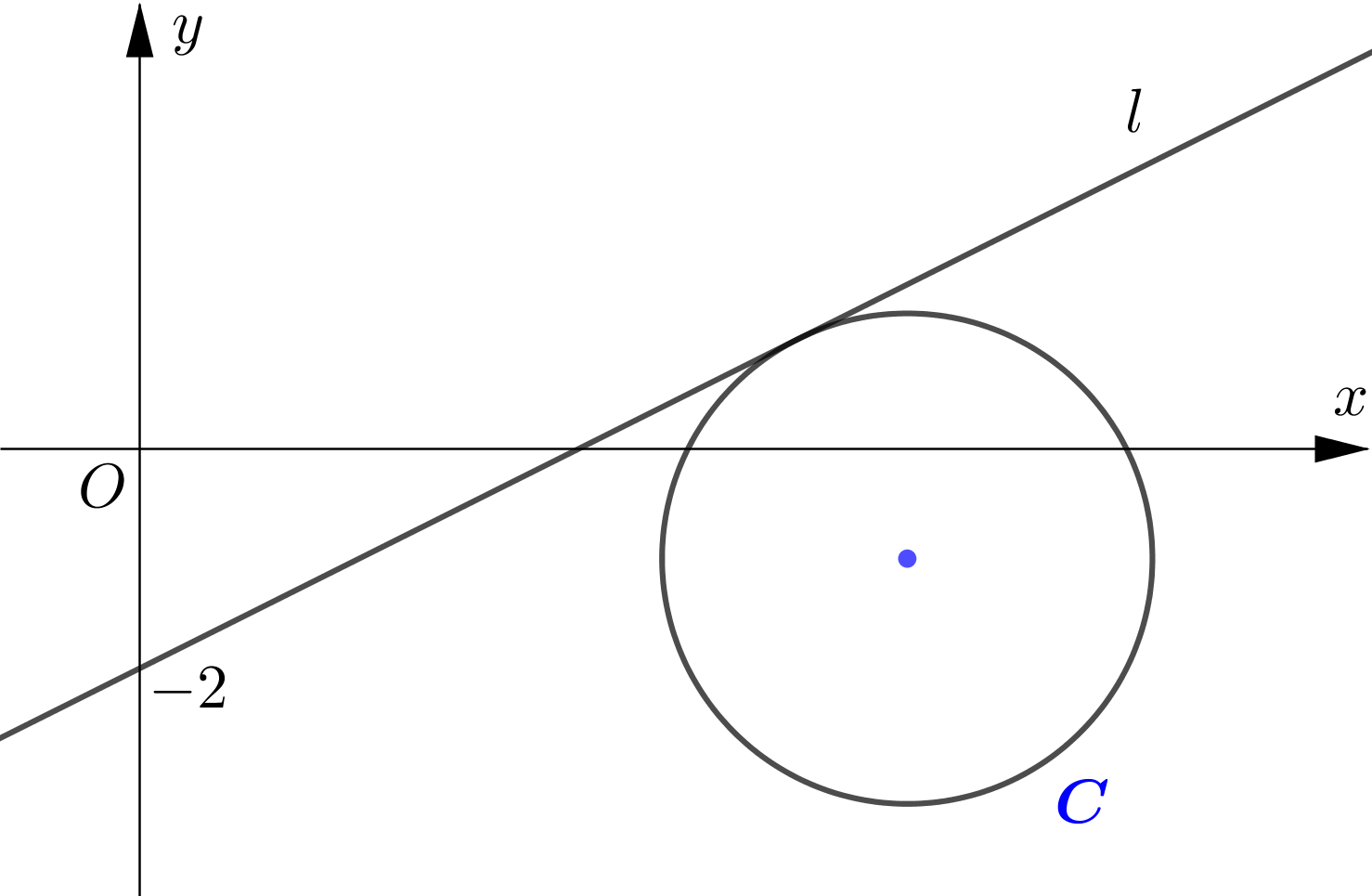
The circle $C$ has equation $(x-7)^{2}+(y+1)^{2}=5$. The line $l$ with positive gradient passes through $(0,-2)$ and is a tangent to the circle. Find an equation of $l$, giving your answer in the form $y=m x+c$.
စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!